

勒让德滤波器(Legendre)的综合设计详解
EMC/EMI设计
描述
文章详细对勒让德滤波器的综合设计进行讲解,解释如何从单调最衰减特性推导出勒让德滤波器的。最后介绍基于Matlab的滤波器设计软件,以低通、带通滤波器为例,展示其功能。给出Github相关链接。
勒让德滤波器特点和用途
勒让德滤波器(Legendre Filter、Papoulis Filter、L Filter)滤波器是1959年Papoulis所提出的一种优化的滤波器(译文:具有单调响应的最优滤波器(Optimum Filters with Monotonic Response)),其幅频特性曲线介于巴特沃斯和第一类切比雪夫滤波器之间,具体来说在通带内具有像巴特沃斯单调频响特性(通带无纹波),但是在阻带具有像切比雪夫滤波器那样具有陡峭的截止特性,这种滤波器在现实中似乎并不常见。
勒让德滤波器逼近
这里采用了特征多项式,定义为,滤波器整体幅度公式为:
约束
1, 是阶多项式(可实现性,在频率增益为0)
2, (低通定义,在频率为0的位置增益为0)
3, (定义低通带宽)
4, 在通带范围内[0, 1]无纹波(勒让德滤波器特征1)
5, 在截止频率点处信号衰减最快(勒让德滤波器特征2)
无纹波
这里需要理解下无纹波从特征多项式上如何理解。
假设在通带内无纹波,表示在区间[0,1]是单调的,即:
或者
衰减最快
这里的衰减最快理解为在处有最大斜率,即:
其中M是最大值。
研究特征多项式的导数
由于约束4和5都有一个明显的特征,就是研究特征多项式的导数会更加方便,所以这里定义:
所以,依据约束4和5得到:
由约束2和约束3,我们得到:
根据基本积分公式可以得到:
所以原问题变为,寻找一个多项式满足如下公式:
由理论推导,奇数阶(偶数阶推导详见:偶数阶单调响应的最优滤波器)勒让德滤波器是一个完全平方,即,这样得到,也就是说问题变为一个函数的平方从0到1的积分为1,需要求这个函数。有很多方法来求解这个方程,首先我们直接求解。
下图是Legendre滤波器和Butterworth滤波器的特征多项式和其导数的对比
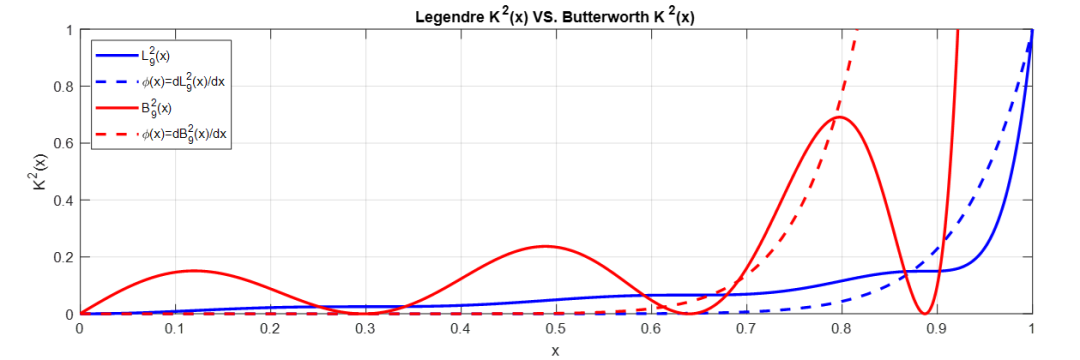
直接优化计算
当然假如我们并不了解勒让德多项式或者雅克比多项式,还是可以直接使用普通多项式来计算,这里以5阶为例来计算,假设所求的多项式的导数为:
在[0,1]范围内恒定大于等于0,天然满足单调条件。然后我们只需要满足积分条件(也就是约束2和3,),即:
由约束4,需要找到上式约束下的最大值:
这里有3个未知数,约束条件只有1个,所以这时一个多参数优化问题,可以有多种优化方法,比较常见的使用拉格朗日乘数法优化,当然也可以用各种数值优化工具,这里使用wolfram alpha:
NMaximize[{(a0 + a1 + a2)^2, Integrate[2*x*(a2*x^4+a1*x^2 + a0)^2, {x, 0, 1}] == 1}, {a0, a1, a2}]
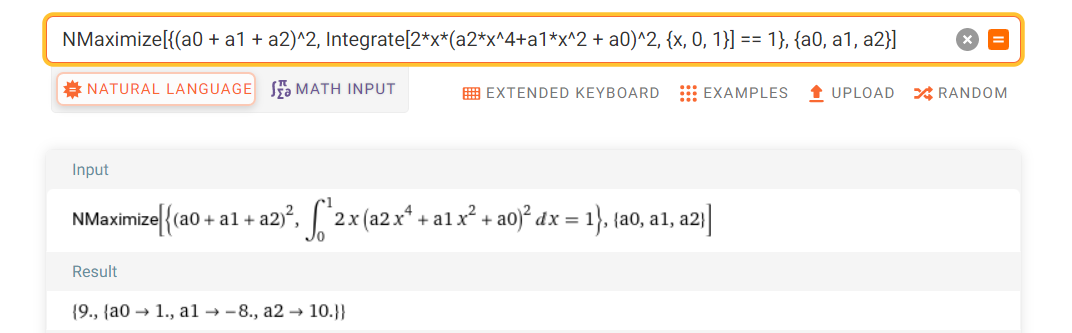
得到
所以:
积分后得到:
用代入得到:
即得到了最终5阶勒让德滤波器特征多项式。
正交多项式求解
要实现这个目标可以使用正交多项式来求解,这是因为正交多项式每个正交项互不干扰,可以单独的调节每个系数达到逼近目的。
勒让德多项式逼近
Papoulis使用了勒让德多项式(Legendre Polynomials)来逼近,勒让德多项式是一组正交多项式。
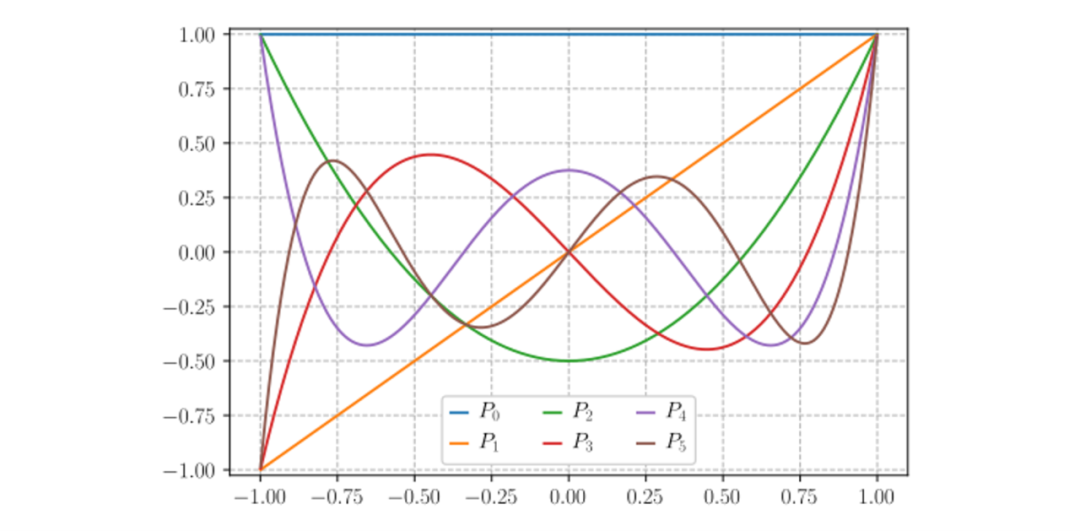
前7阶勒让德多项式为:
| 多项式阶数 | |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
最终我们需要求解的就可以写成一系列的的多项式的组合。
这里看似将公式复杂化,但是实际上简化了计算,原因在于满足从[-1,1]积分为0,所以当上式展开积分后,各个交叉项由于多项式不相关从而相互抵消为0,只有自身乘以自身的项保留了下来。
上式将一个积分转化为一个普通代数表达式,使用勒让德多项式极大简化了计算。
到这一步大家解法都统一了,这是一个带约束的优化问题,使用拉格朗日乘数法即可解决。
这里以为例展示下计算过程(这里,勒让德多项式到):
约束为
最大化
即最大化(引入拉格朗日乘数)
分别对求偏导,令其等于0(求极值点),并列出公式:
化简得到:
代入最后一个公式得到:
解得:
代入得到:
由于勒让德多项式是定义在[-1,1]上,所以需要将其转换到[0,1]区间,令,积分求解得到特征多项式:
frac{1}{8}int_{-1}^{2w^2-1}{1+3x}^2dx
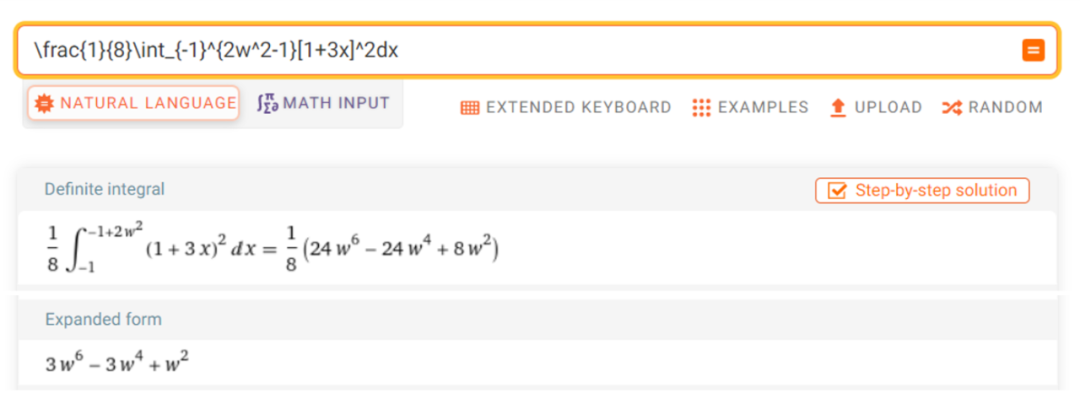
位移雅可比多项式逼近
FUKADA使用了位移雅可比多项式(Shifted Jacobi Polynomials)来逼近,位移雅可比多项式也是一组正交多项式,它包含两个参数,配置不同的参数就会表现出不同特征多项式,位移雅可比多项式可以包含几乎所有的滤波器多项式。下面列出位移雅克比多项式的递推公式:
其中的系数为:
当且时,上式就为勒让德多项式。
其他推导方式和之前勒让德方式相同。
但是这里带出一个概念,即对于雅克比多项式,满足正交性质,但是应用更加广泛:
公式中的是Kronecker delta符号,表示只有当时才为1,其他都为0.为权函数
在勒让德多项式中,,即对于整个[-1,1]范围内权重相同,在不同应用场景中,我们可以根据需要选择不同的优化策略。下图展示了不同参数情况下权重的变化:
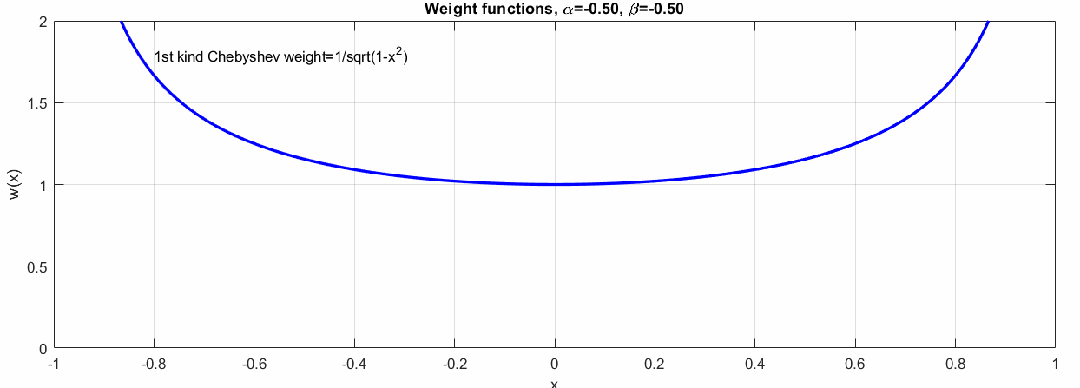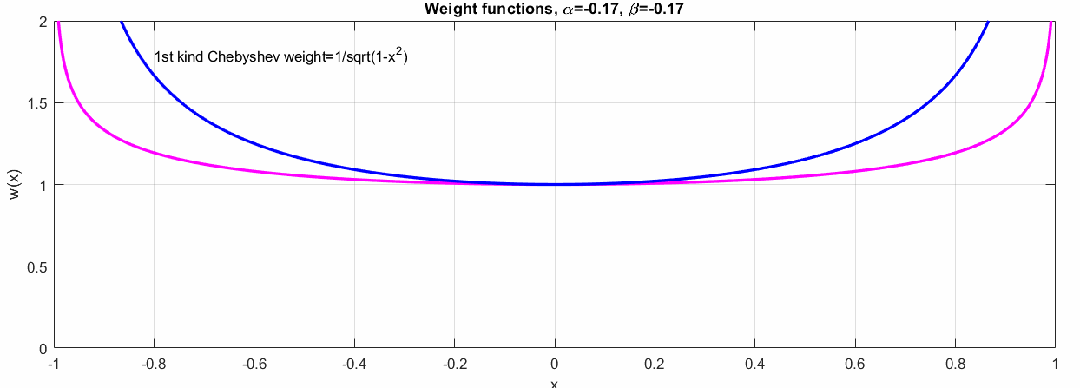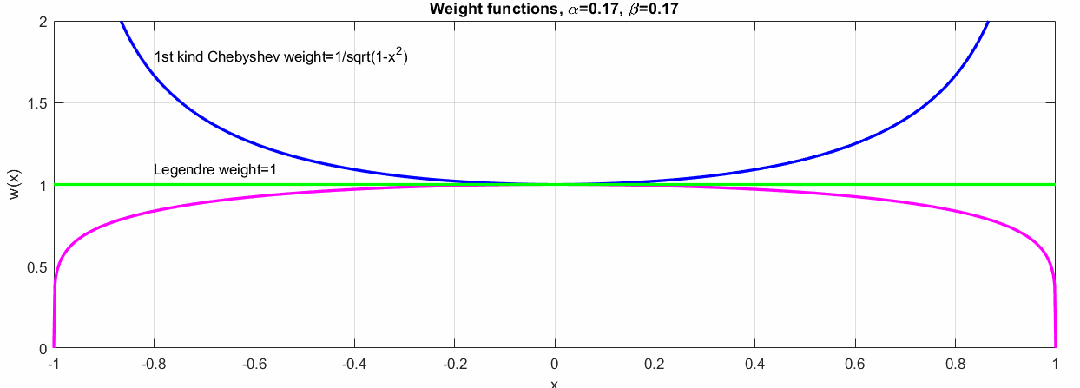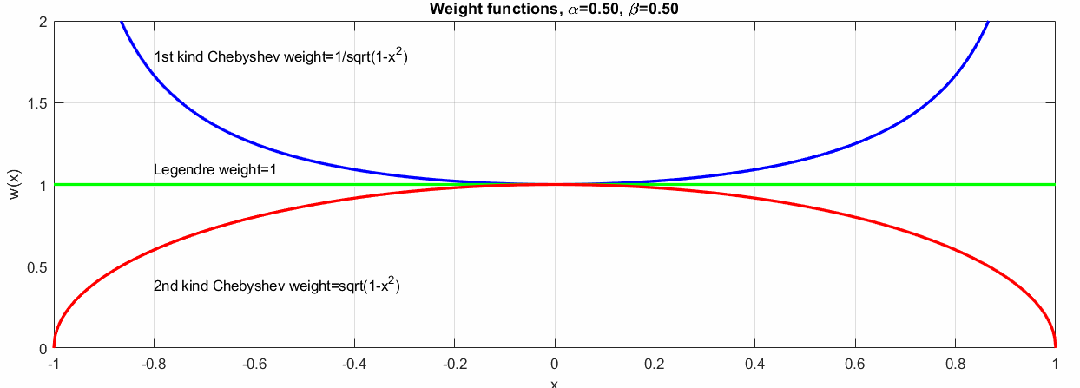
当权重且时,多项式是第一类切比雪夫多项式,多项式在两端的权重比较大,当权重时,多项式就是第二类切比雪夫多项式,多项式在两端的权重小。
在勒让德滤波器中,权函数为1,表面在整个[-1,1]区间内,所有点贡献都相同,这样综合出来的必定是无纹波的滤波器。可以这样直观的理解,假如区间内存在纹波,那么积分值必定会比没有纹波的大,因为函数的平方我们可以理解为对函数求其有效值,那么若存在纹波,那么有效值就等于直流分量加上交流分量,这两者相加就必定大于其中之一。
使用公式也可以简单的说明这一点,假设是一个直流信号,幅度值在[0,1]范围内均为,那么假设存在一个脉动直流信号在[0,0.5]范围内是,在(0.5,1]范围内是,必定存在即。也即是说,通过平方操作,大的值比小的值放大得更大,大的值变得更加突出。在这样的优化条件下,保持积分值不变,原函数在端点取得最大值,函数将呈现单调变化。
本节中,通过采用不同的参数设置,位移雅可比多项式可以得到不同特性的滤波器。
勒让德滤波器评价
Papoulis首先第一次提出了这种滤波器就得到很多学者的关注,其中相继发表了多篇关于单调滤波器的设计,这里发展出来很多优化了的单调滤波器,比如LSM(Least-Squares-Monotonic)滤波器,H滤波器,这些滤波器各具特点,总结下来就是我们前面给出的不同约束5所综合下来的滤波器。
比如H滤波器(本系列文章中有翻译)就是将约束5修改为:
5, 在渐近频率点处信号衰减最快(也即特征多项式最高系数最大,H滤波器特征)
LSM滤波器(本系列文章中有翻译)就是将约束5修改为:
5, 在通带范围内曲线所包围的面积最小(也即在整个通带范围内滤波器反射或插损最小,LSM滤波器特征)
同理我们可以将巴特沃斯滤波器纳入到这种单调滤波器体系,将约束5修改为:
5, 在0频率处响应最平坦(Butterworth滤波器特征)
可以说Papoulis开创了一种新的滤波器约束规则,丰富了滤波器的种类。总的来说,这种单调滤波器也属于幅度逼近。
最近几年有论文指出勒让德滤波器除了阶梯的衰减特性外没有任何其他优势,大家有兴趣可以看看,本公众号已经将其翻译为中文《在连续时间域中比较Papoulis滤波器和Chebyshev滤波器》。
单调滤波器系数和零极点
目前还没有统一的公式去计算勒让德滤波器的特征多项式,但是可以通过数值计算的办法计算出系数来,以下提供了生成系数的Matlab代码,需要具体源码的可以去Github上下载。
使用Matlab求解勒让德特征多项式系数
%--------------------------------------------------------------------------
% Edited by bbl
% Date: 2023-06-11(yyyy-mm-dd)
% 勒让德滤波器系数设计
% 注意返回值低次在前,高次在后
%--------------------------------------------------------------------------
function [Ln] = funGenLegendreCharacteristicPoly(FilterOrder)
% Initialize coefficient vector
coefficients = ((1:FilterOrder).*2 - 1);
% Define coefficient for normalization
if mod(FilterOrder, 2) == 1
% Odd polynomial order
half_order = (FilterOrder - 1) / 2;
norm_coefficient = 1 / (sqrt(2 * (half_order + 1) * (half_order + 1)));
else
% Even polynomial order
half_order = FilterOrder / 2 - 1;
norm_coefficient = 1 / sqrt((half_order + 1) * (half_order + 2));
% Check if the half_order is odd or even
if mod(half_order, 2) == 1
% Odd
coefficients(1:2:end) = 0;
else
% Even
coefficients(2:2:end) = 0;
end
end
% Apply normalization to coefficients
coefficients = coefficients * norm_coefficient;
% Initial value for the Phi
Phi = 0;
% Generate polynomial and add to Phi
for i = 1:half_order + 1
current_coefficient = coefficients(i);
legendrePoly = JacobiPoly(i - 1, 0, 0); % Gen legendre polynomial
Phi = polyadd(Phi, current_coefficient * legendrePoly);
end
% Calculate Phi^2
Phi_squared = conv(Phi, Phi);
% For even polynomial order, multiply Phi_squared by (x+1)
if mod(FilterOrder, 2) == 0
Phi_squared = conv(Phi_squared, [1,1]);
end
% Calculate the integral of Phi_squared
integral_of_Phi_squared = polyint(Phi_squared, 0);
% Define the range for polyval function
lower_range = -1;
upper_range = [2, -1];
% Calculate polyval for lower and upper ranges
D = polyval(integral_of_Phi_squared, lower_range);
U = substitute_poly(integral_of_Phi_squared, upper_range);
% Final result
Ln0 = polyadd(U, -D);
nLn = length(Ln0);
Ln = zeros(1, nLn*2-1);
Ln(3:2:end) = fliplr(Ln0(1:end-1));
Ln(1) = Ln0(end);
end
运行结果如下:
>> [Ln] = funGenLegendreCharacteristicPoly(5)
Ln =
0 0 1 0 -8 0 28 0 -40 0 20
也就是:
这里给出数值计算出的勒让德滤波器前7阶滤波器多项式(注意这里):
| 滤波器阶数 | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
不同阶数滤波器频响如下(图中红色曲线是勒让德滤波器频响,绿色曲线是巴特沃斯频响,蓝色曲线是切比雪夫I纹波为的频响):
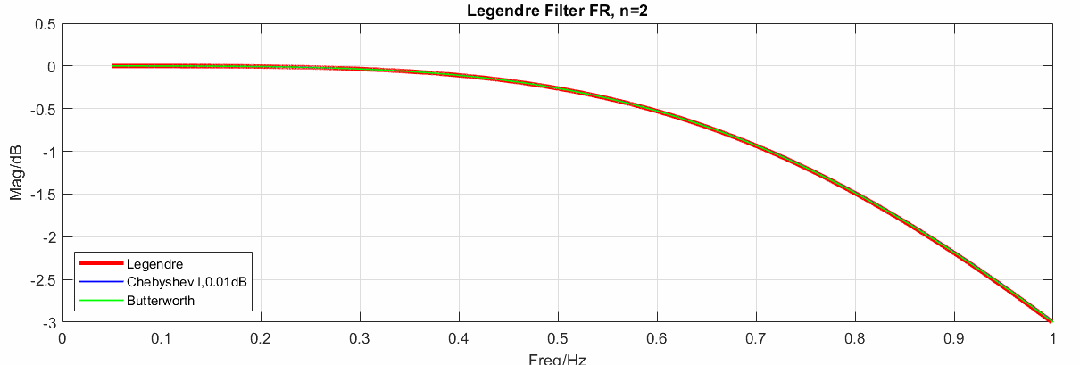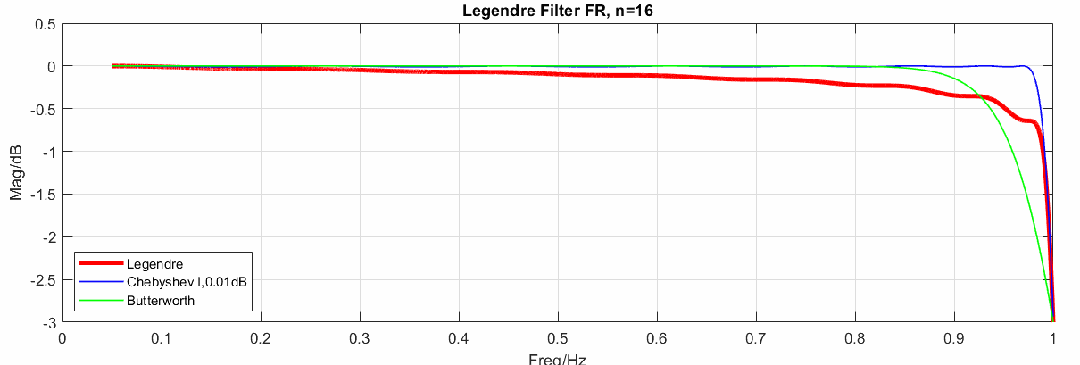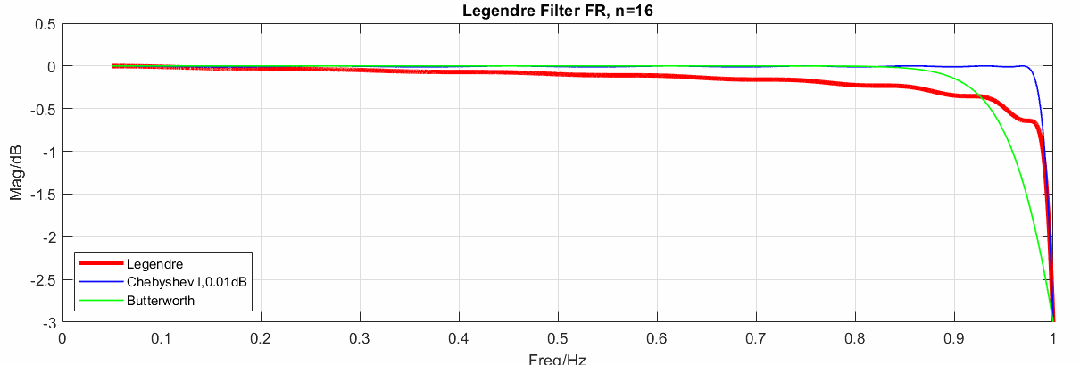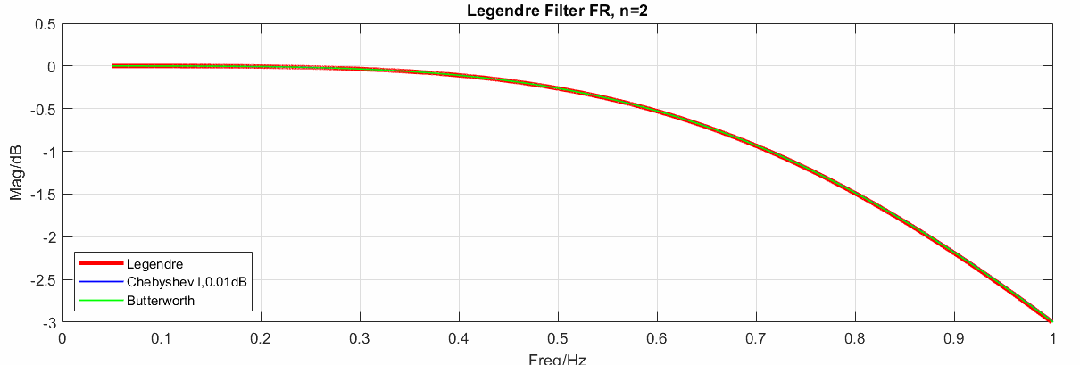
事实上,勒让德滤波器的频率响应并未达到我们预期的优秀程度,从图中可以看到对比切比雪夫滤波器,勒让德滤波器没有优势,因此,一些学者批评这只是一种适合学术研究,而在实际应用中并无优势的滤波器。
在s平面取其左半边极点得到前7阶勒让德滤波器系数为(, 其中的极点等于的做半边极点):
| 滤波器阶数 | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
前7阶勒让德滤波器极点为():
| 滤波器阶数 | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
零极点变化动图(图中红色点是勒让德滤波器极点,蓝色和绿色分别是切比雪夫滤波器极点和巴特沃斯滤波器极点分布,猜测勒让德滤波器极点也是分布在一个椭圆上,注意这里的零极点图横坐标是虚轴,纵坐标为实轴):
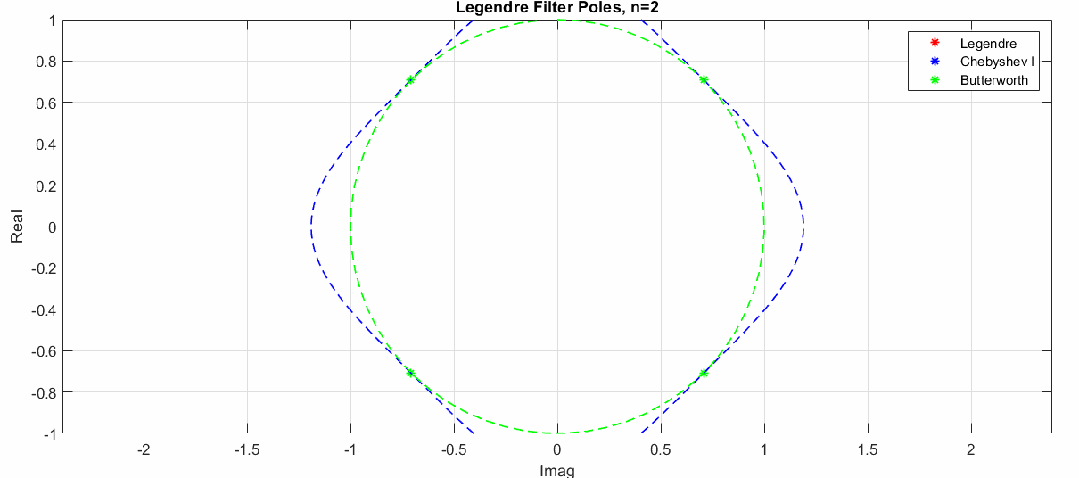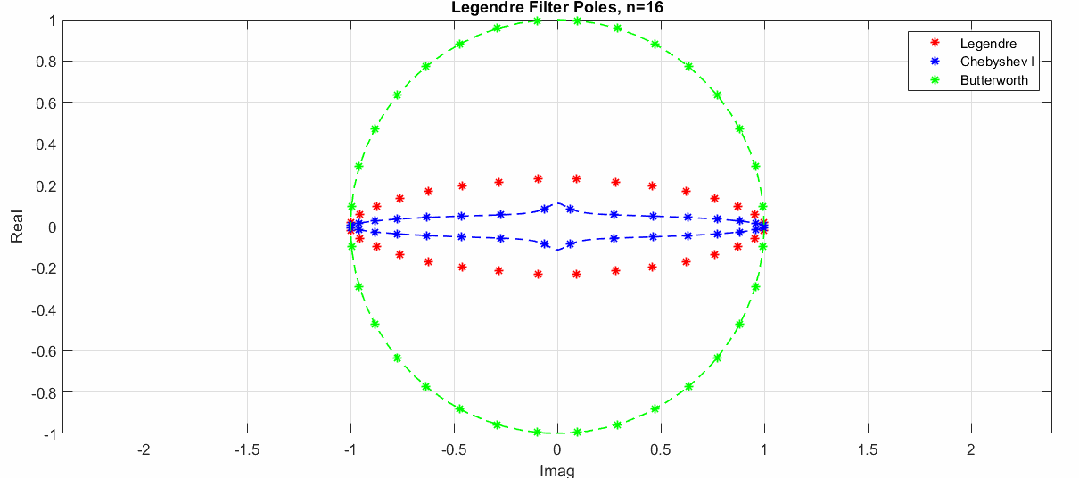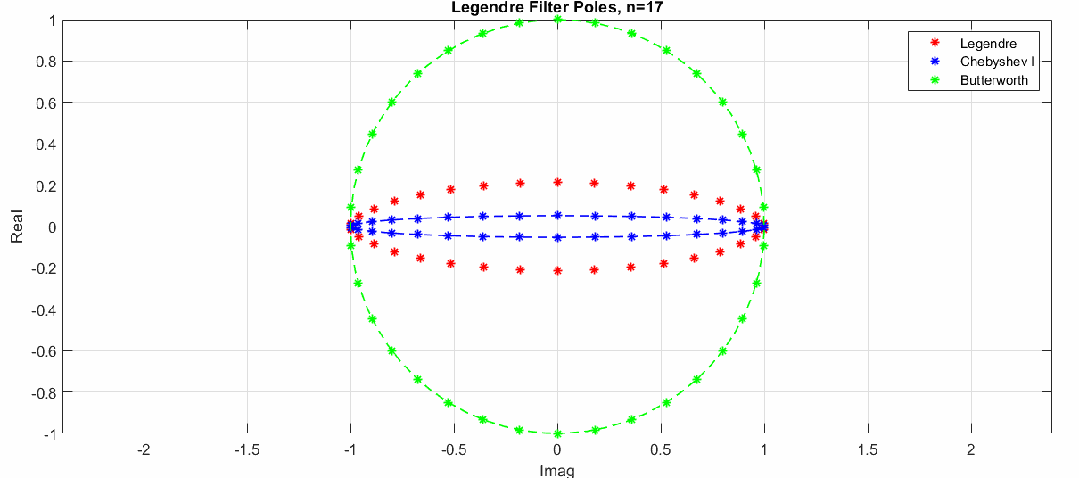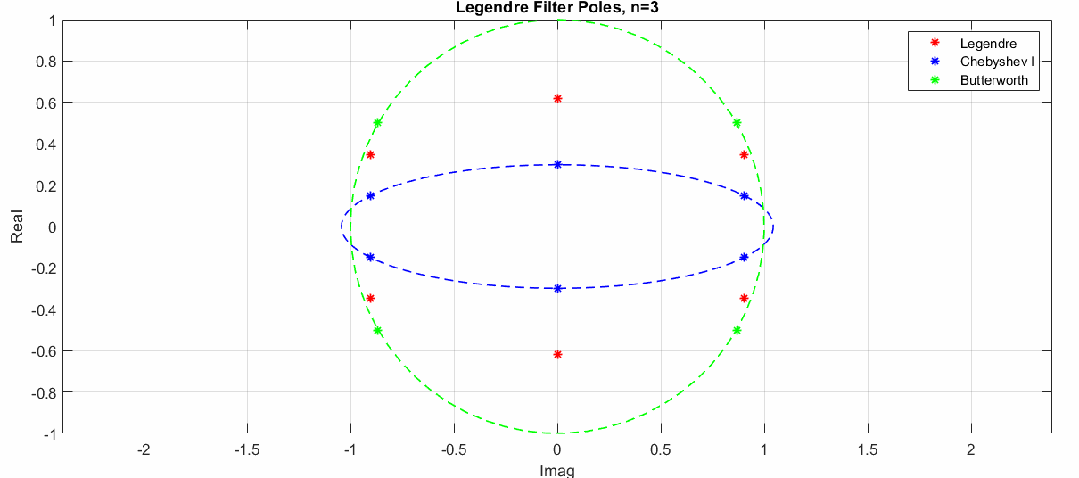
这里通过调整切比雪夫滤波器纹波大小,验证了猜测,勒让德滤波器极点分布近似在一个椭圆上:
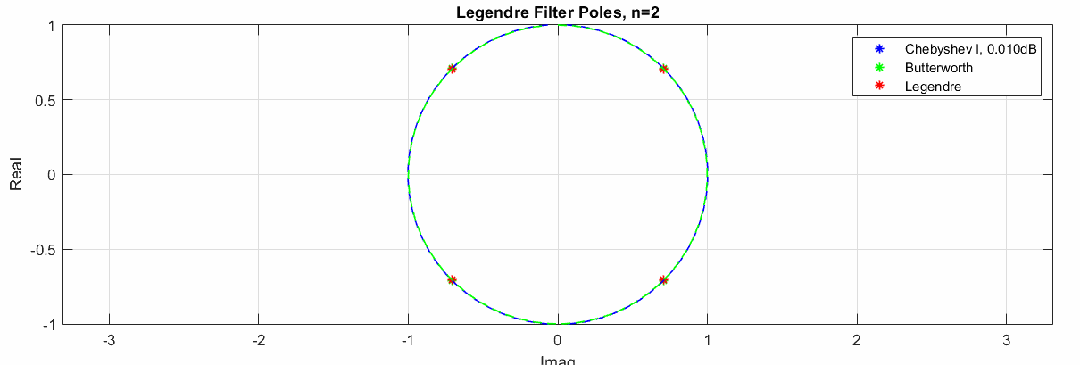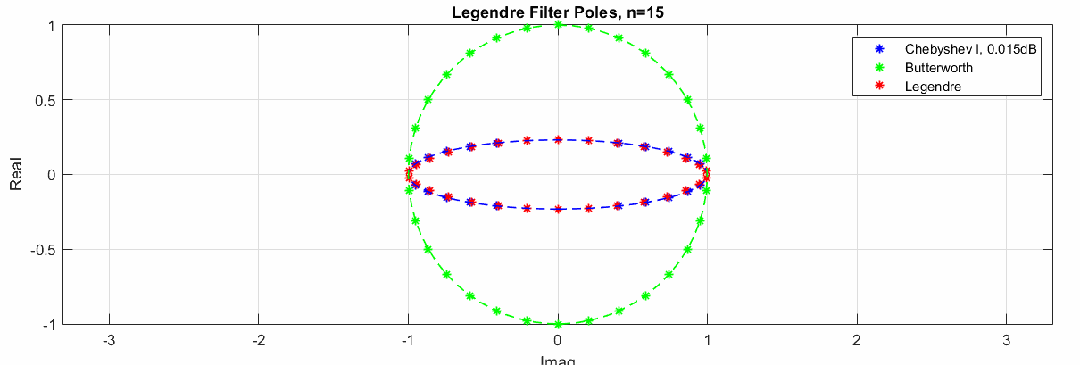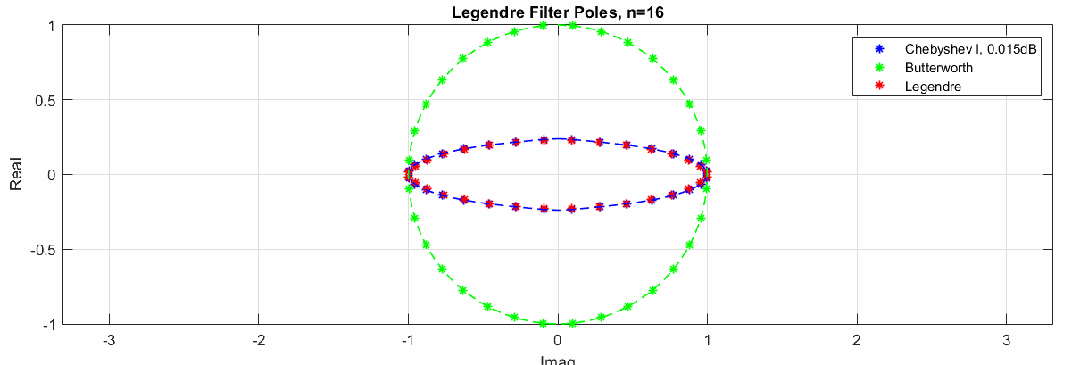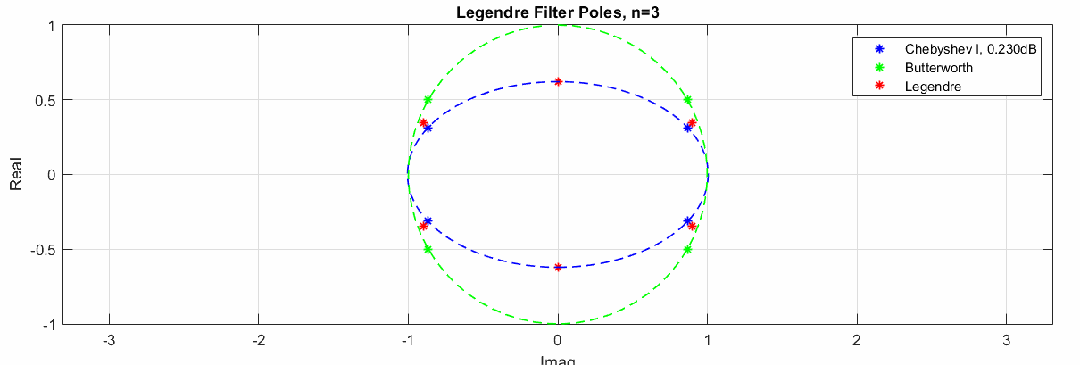
下图是不同类型滤波器的零极点分布图,红色曲线和点是5阶勒让德滤波器极点分布,可见勒让德滤波器的极点在巴特沃斯滤波器和切比雪夫滤波器之间:
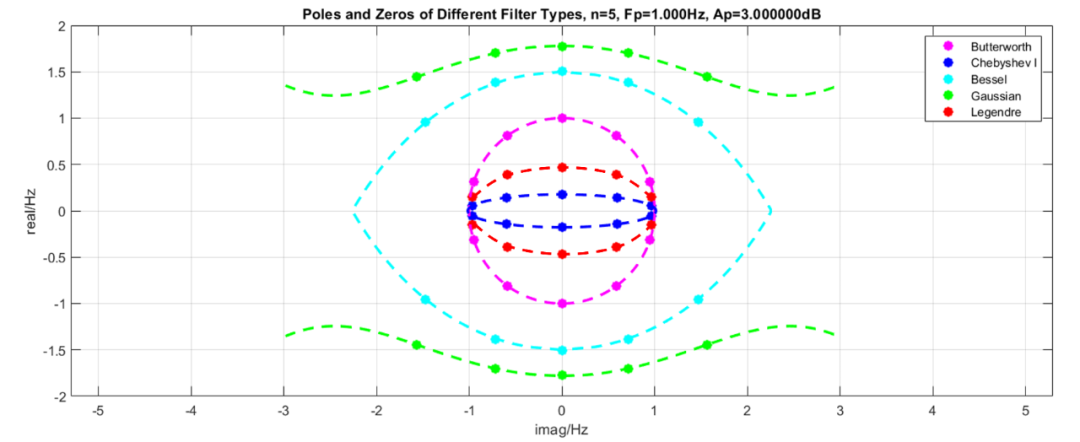
勒让德滤波器综合
勒让德波器综合和巴特沃斯滤波器一样,属于全极点滤波器,所以这里仅仅列出一个简单的3阶勒让德滤波器综合实例,以供参考:
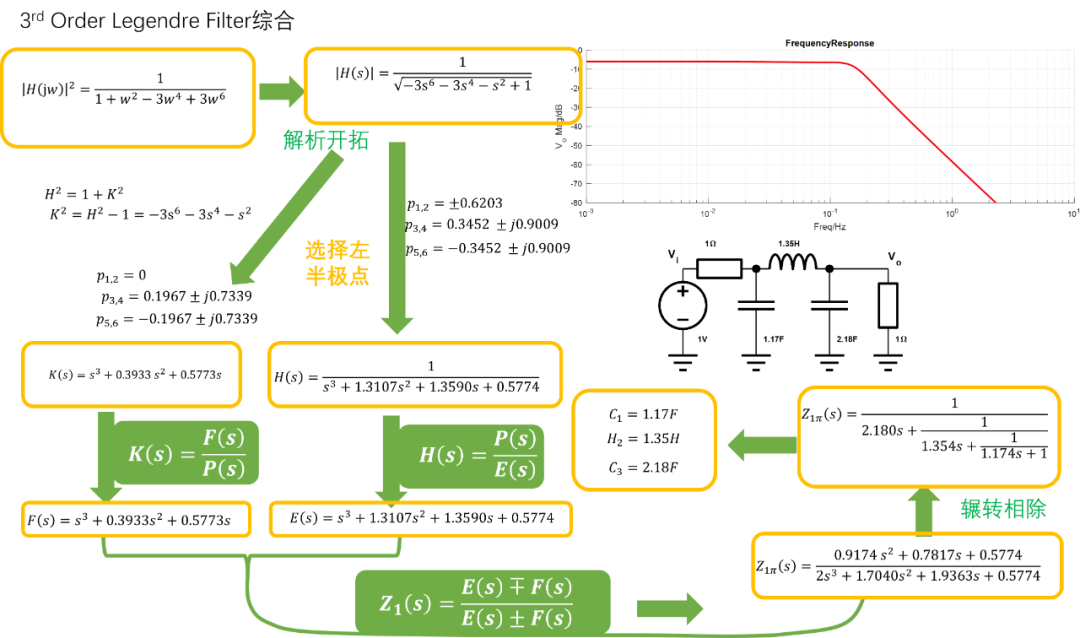
勒让德滤波器设计软件
基于Matlab的appdesign工具开发了一套滤波器设计软件, 主要特点是:
支持勒让德滤波器(Legendre Filter)、高斯滤波器(Gaussian Filter)、贝塞尔滤波器(Bessel Filter)、椭圆函数滤波器(Elliptic/Cauer Filter)、切比雪夫滤波器(Chebyshev I)、逆切比雪夫滤波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯滤波器(Butterworth)设计
支持4种不同滤波器通带类型(LPF,HPF,BPF,BRF)设计
T型和PI型结构滤波器随意切换
可以设置阻带衰减决定滤波器阶数
可以设置通带衰减来综合滤波器
可以随意配置负载和终端阻抗, 并支持一端接载(源端电阻短路, 源端电流源, 终端开路, 终端短路)设计
可以幅频响应分析、零极点分析、瞬态分析
可以显示理想频率响应、零极点和实际仿真的的频率响应、零极点
可以支持实际标准器件逼近设计
Legendre LPF设计举例
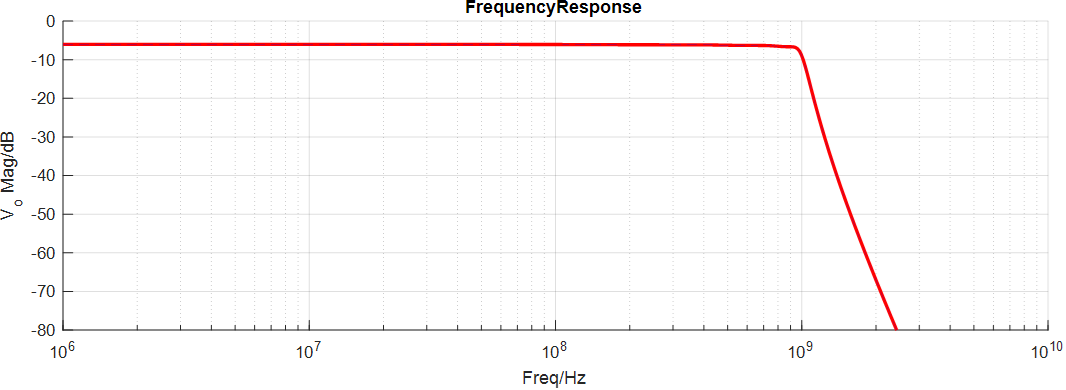
设计一款-3dB截止频率为1GHz, 7阶低通Legendre滤波器,输入输出阻抗为50欧姆,设计过程如下:
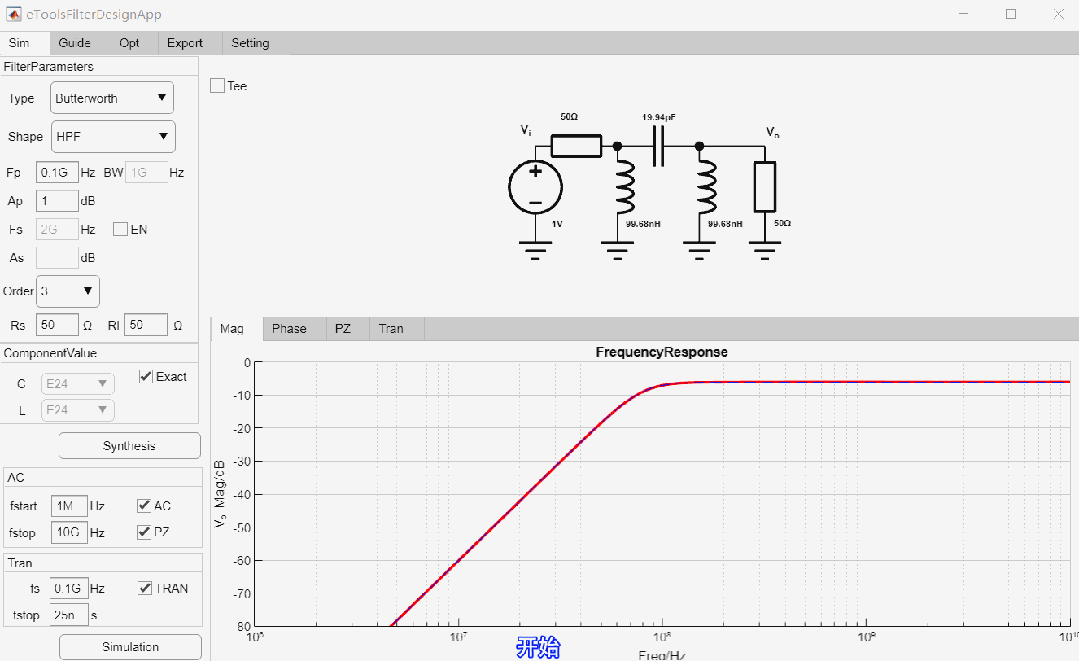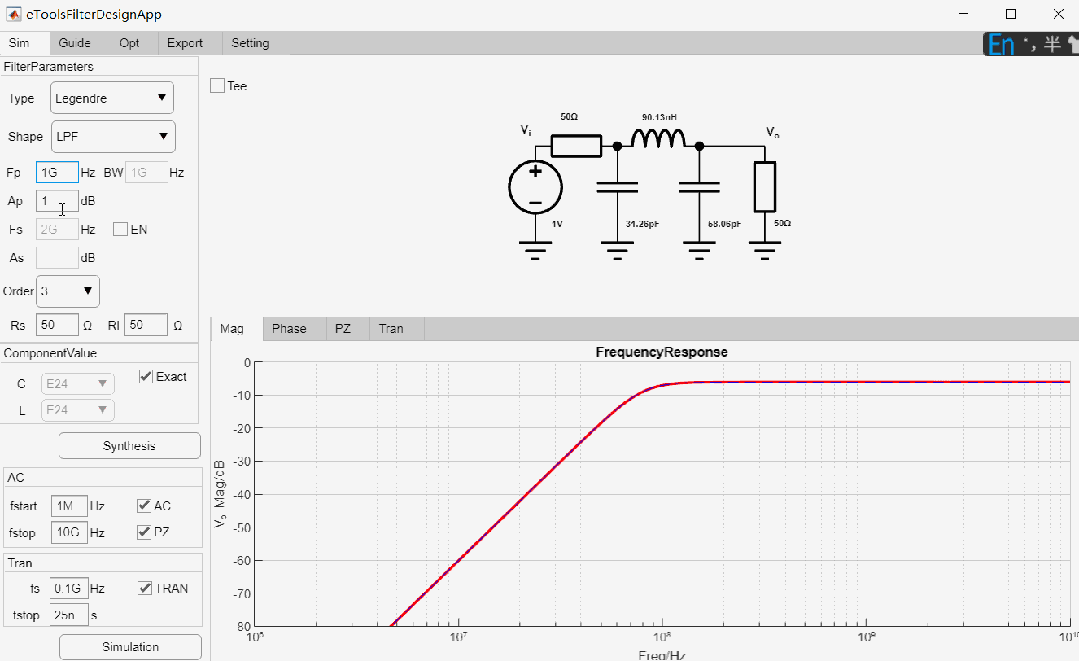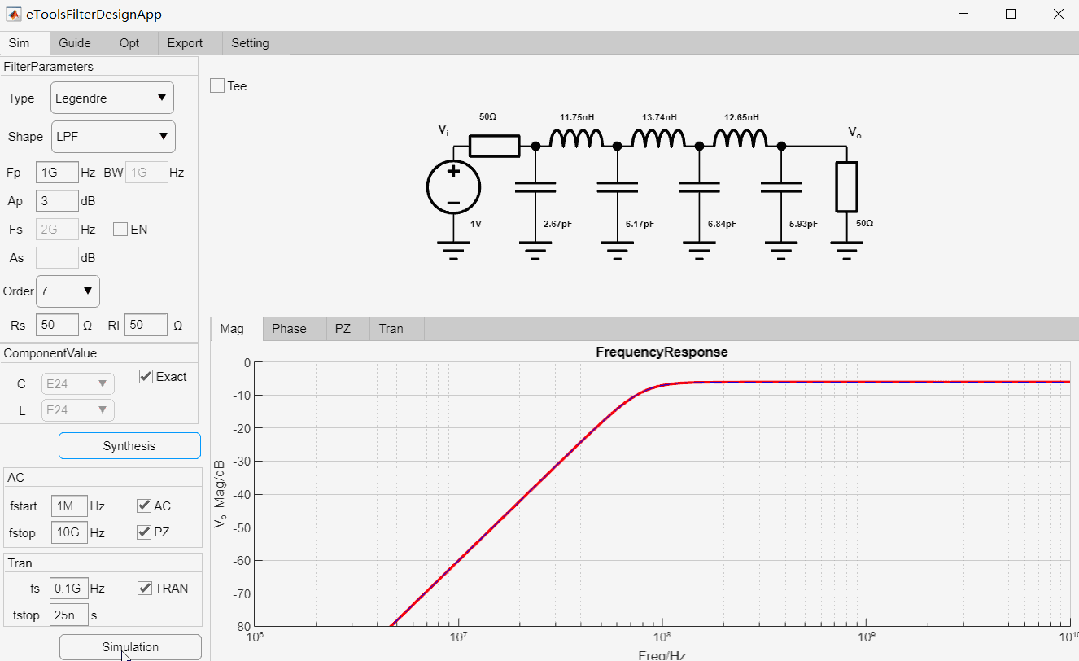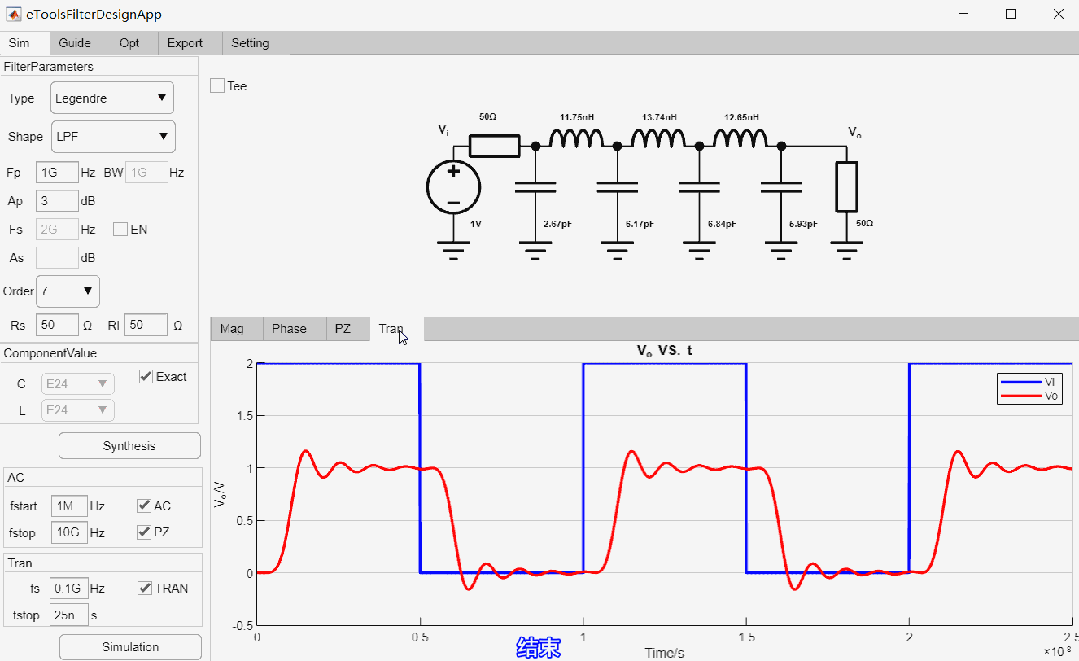
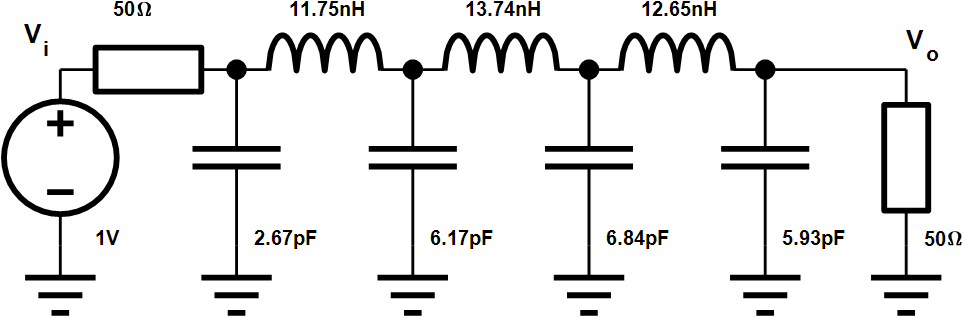
最终设计参数如下:
勒让德滤波器瞬态仿真结果:
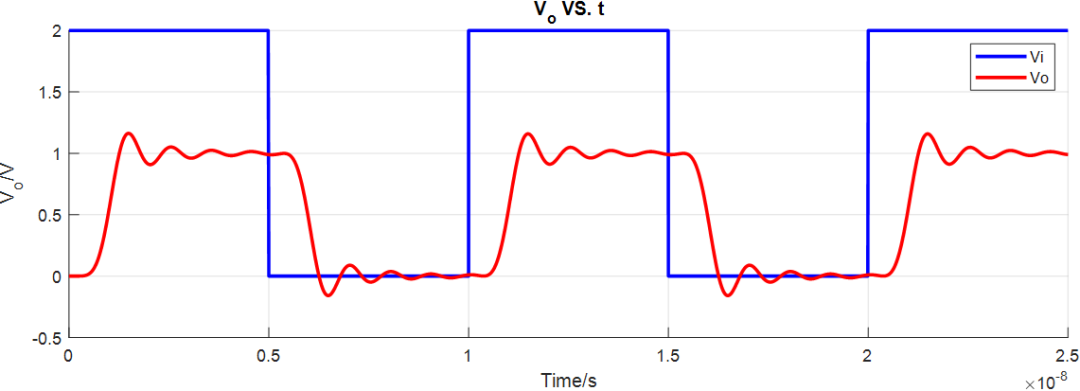
勒让德滤波器AC仿真结果:
Legendre BPF设计举例
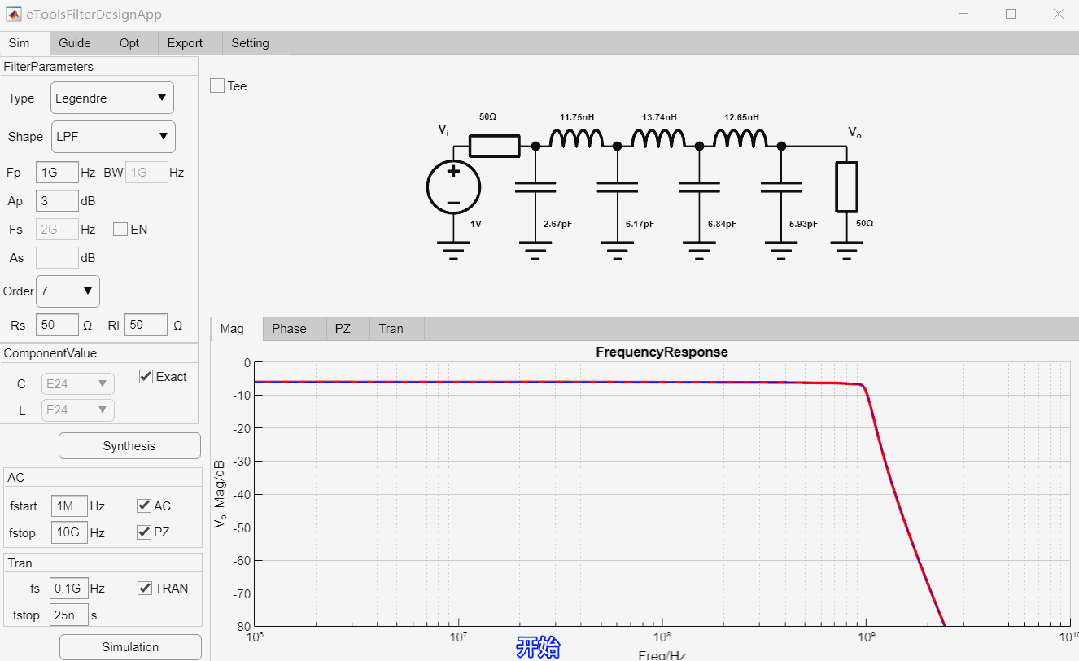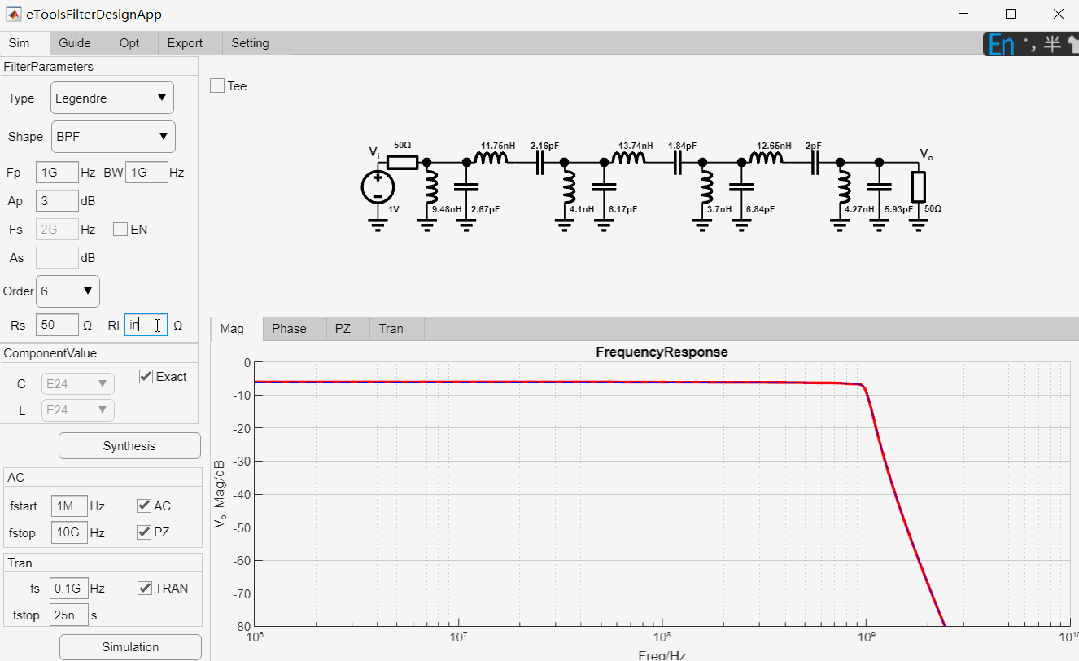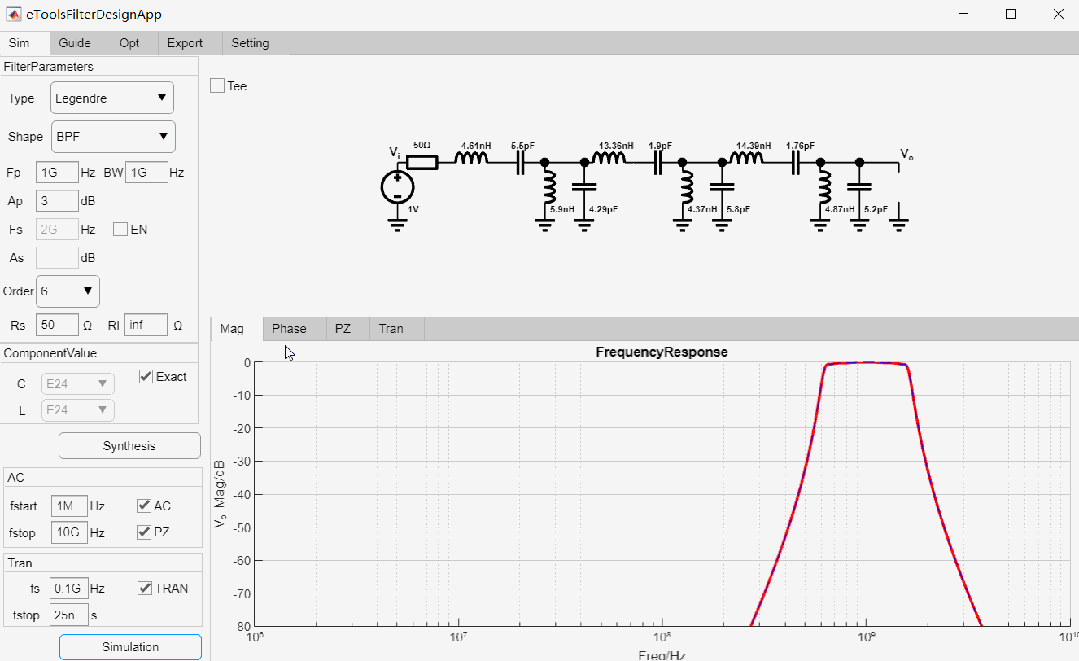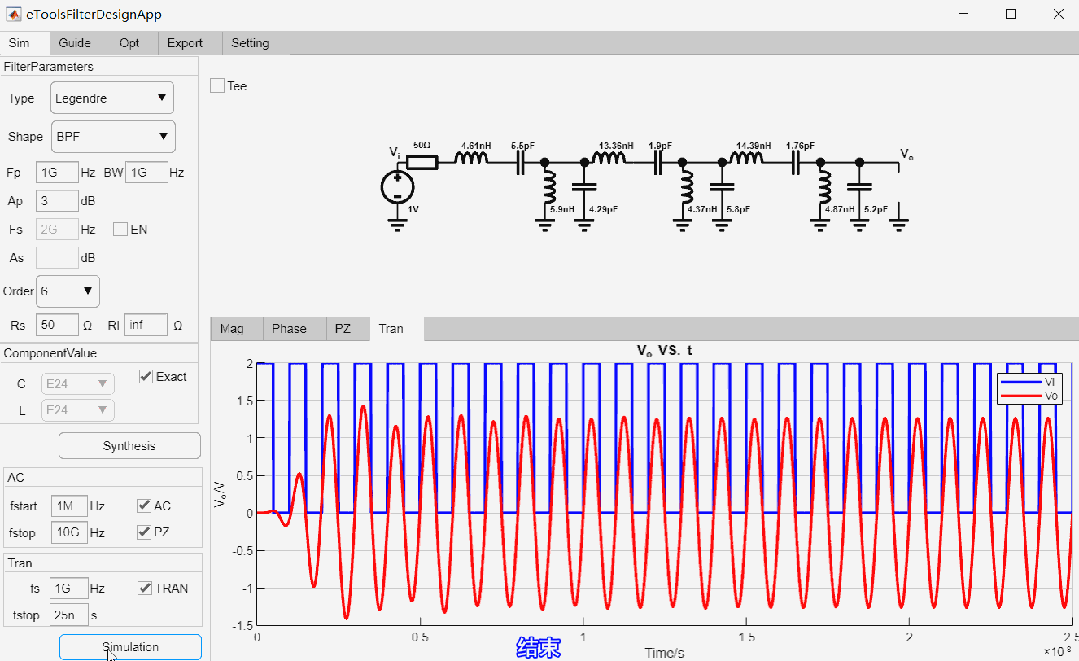
设计6阶带通Legendre滤波器, 中心频率为1GHz,带宽为1GHz,50欧姆输入,输出阻抗为高阻,最后进行瞬态仿真,设计过程如下:
最终设计参数如下:

AC仿真结果:
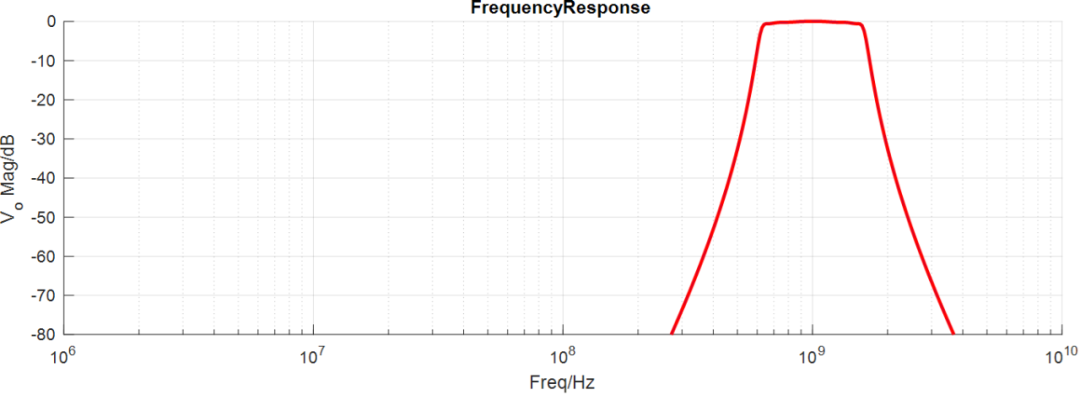
瞬态仿真结果:
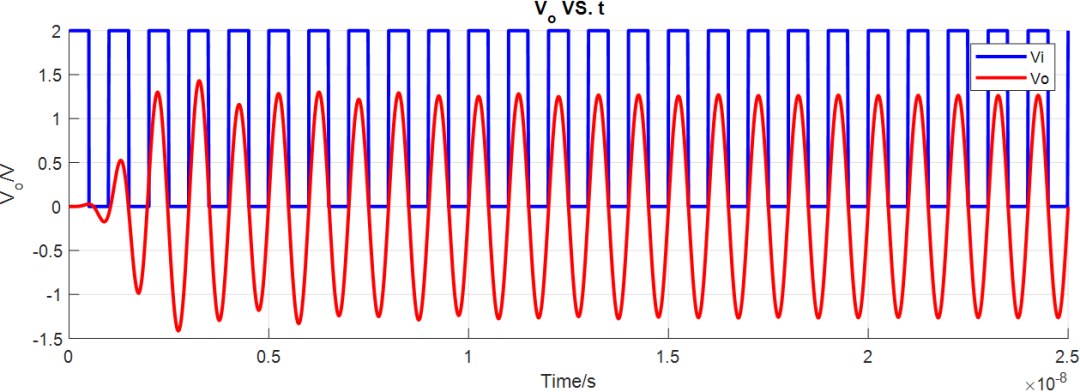
程序的Matalb源码已经上传GitHub中,有兴趣的同学可以下载试用体验,当然也欢迎技术交流。
直线型滤波器设计预告
回到我们开启这一主题的初衷(模拟无源滤波器设计(一)),想要实现一个直线型滤波器设计,现在做了这么多铺垫,我们终于有能力设计出这样一个直线型滤波器了。直线型滤波器不也是一种单调滤波器吗!只要让斜率小于0即可。但是我们应该也需要考虑到直线型滤波器实际上会出现频率响应大于0的情况出现,这里解决方案类似于偶数阶切比雪夫滤波器遇到的问题那样,实际上偶数阶低通切比雪夫滤波器在综合时就出现了0频率处幅度小于0的情况,当时得到的结果是,当滤波器两边不匹配时,即存在直流衰减情况下是可以实现的。所以我们可以列出直线型滤波器设计约束规则:
1, 是阶多项式(可实现性,在频率增益为0)
2, (直线的第一个坐标,在频率为0的位置增益为IL, )
3, (直线的第二个坐标,在频率为1的位置增益为1,即最大值)
4, 在通带范围内[0, 1]无纹波(直线特征)
编辑:黄飞
-
切比雪夫滤波器的综合设计2022-10-10 10309
-
模拟无源滤波器设计(九)-Gaussian滤波器设计详解2023-05-28 7282
-
是德滤波器调谐软件2019-07-11 0
-
光滤波器,什么是光滤波器2010-04-02 2330
-
采用感应滤波设计的双调谐滤波器综合技术2010-05-13 1742
-
详解FIR滤波器和IIR滤波器的区别2017-05-03 2453
-
无线通信用SAW滤波器的分析与设计详解2017-08-30 923
-
带通滤波器威廉希尔官方网站 图大全(三款带通滤波器威廉希尔官方网站 设计原理图详解)2018-03-26 319659
-
详解滤波器的种类,它的种类都有哪些2021-07-09 3791
-
一阶有源滤波器原理详解2022-11-14 2810
-
二阶有源高通滤波器原理详解2022-11-18 3863
-
二阶有源带通滤波器原理详解2022-11-21 4149
-
Elliptic滤波器设计详解2023-03-06 6249
-
在连续时间域中比较Papoulis滤波器和Chebyshev滤波器2023-06-10 1490
-
偶数阶勒让德滤波器的设计介绍2023-06-11 401
全部0条评论

快来发表一下你的评论吧 !

