基准数据集(CORR2CAUSE)如何测试大语言模型(LLM)的纯因果推理能力

 

因果推理是人类智力的标志之一。因果关系NLP领域近年来引起了人们的极大兴趣，但其主要依赖于从常识知识中发现因果关系。本研究提出了一个基准数据集(CORR2CAUSE)来测试大语言模型(LLM)的纯因果推理能力。其中CORR2CAUSE对LLM来说是一项具有挑战性的任务，有助于指导未来关于提高LLM纯粹推理能力和可推广性的研究。

简介

因果推理

因果推理是推理的一个基本方面，其涉及到在变量或事件之间建立正确的因果关系。大致可分为两种不同的方式的因果关系：一种是通过经验知识，例如，从常识中知道，为朋友准备生日派对会让他们快乐；另一种是通过纯粹的因果推理，因果关系可以通过使用因果推理中已知的程序和规则进行形式化的论证和推理得到。例如，已知A和B彼此独立，但在给定C的情况下变得相关，那么可以推断，在一个封闭系统中，C是A和B共同影响的结果，如下图所示。

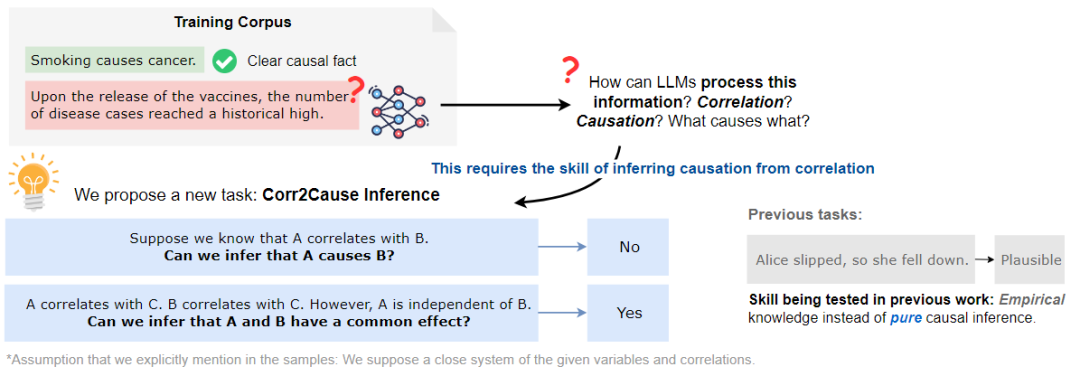
想象上图中的场景，在训练语料库中有大量的相关性，比如疫苗这个词与疾病病例数量的增加有关。如果认为LLM的成功在于捕捉术语之间的大量统计相关性，那么关键但缺失的一步是如何处理这些相关性并推断因果关系，其中一个基本的构建块是CORR2CAUSE推断技能。

本文将这项任务表述为NLP的一项新任务，即因果关系推理，并认为这是大语言模型的必备技能。

贡献

基于CORR2COUSE数据集，本文探讨了两个主要的研究问题：

(1)现有的LLM在这项任务中的表现如何？

(2)现有的LLM能否在这项任务中重新训练或重新设定目标，并获得强大的因果推理技能？

本文的主要贡献如下：

(1)提出了一项新任务，探讨LLMs推理能力的一个方面，即纯因果推理；

(2)使用因果发现的见解组成了超过400K个样本的数据集；

(3)在数据集上评估了17个LLM的性能，发现它们的性能都很差，接近随机基线；

(4)进一步探讨了LLM是否可以通过微调来学习这项技能，发现LLM无法在分布外扰动的情况下稳健地掌握这项技能，本文建议未来的工作探索更多方法来增强LLM中的纯因果推理技能。

因果推理预备知识

因果模型有向图(DGCM)

有向图形因果模型是一种常用的表示方法，用于表示一组变量之间的因果关系。给定一组N个变量X={X1,...,XN}，可以使用有向图G=(X，E)对它们之间的因果关系进行编码，其中E是有向边的集合。每条边ei,j∈E代表一个因果联系Xi→Xj，意味着Xi是Xj的直接原因。

D-分离与马尔可夫性质

D-Separation(D-分离)

D分离是图模型中的一个基本概念，用于确定在给定第三组节点Z的情况下，DAG中的两组节点X和Y是否条件独立，其中这三组节点是不相交的。

Markov Property(马尔可夫性质)

DAG中的马尔可夫性质表明每个节点Xi在给定父节点的情况下有条件地独立于其非后代，。使用马尔可夫属性，可以将图中所有节点的联合分布分解为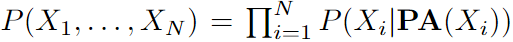为了从概率分布中推断因果图，一个常见的假设是置信度，即从概率分布中的独立关系中推断图中所有D-分离集的有效性。在本文的工作中，也采用了这个广泛的假设，它适用于大多数现实世界的场景。

Markov Equivalence of Graphs(图的马尔可夫等价)

如果两个DAG有相同的联合分布P(X)，则将两个DAG表示为马尔可夫等价。相互等价的马尔可夫 DAG集称为马尔可夫等价类(MEC)。同一MEC中的因果图可以很容易地识别，因为它们具有相同的骨架(即无向边)和V结构(即A→B←C形式的结构，其中A和C不连接)。

因果发现

因果发现旨在通过分析观测数据中的统计属性来学习因果关系。它可以通过基于约束的方法、基于分数的方法或其他利用功能因果模型的方法来实现。

为了从相关性(用自然语言表示)推断因果关系，本研究的数据集设计基于广泛使用的Peter Clark(PC)算法。其使基于条件独立原则和因果马尔可夫假设，这使它能够有效地识别给定数据集中变量之间的因果关系。该算法首先从所有变量之间的完全连通无向图开始。然后，如果两个变量之间存在无条件或有条件的独立关系，它就消除了它们之间的边。然后，只要存在V形结构，它就会定向定向边。最后，它迭代地检查其他边的方向，直到整个因果图与所有统计相关性一致。

数据集构建

任务定义

给定一组N个变量X={X1,...,XN}，一个关于变量之间所有相关性的声明s，以及一个描述变量Xi和Xj对之间的因果关系r的假设h。该任务是学习一个函数f(s,h)→v，它将相关语句和因果关系假设h映射到它们的有效性v∈{0,1}，如果该推理无效，则取值0，否则为1。

数据生成过程

数据生成过程如下图所示，首先选择变量的数量N，并生成所有具有N个节点的唯一DGCM。然后，从这些图中收集所有D分离集。对于MEC到因果图的每个对应关系，根据MEC中的统计关系组合相关语句，并假设两个变量之间的因果关系，如果假设是MEC中所有因果图的共享属性，则有效性v=1，如果对于所有MEC图的假设不一定为真，则v=0。

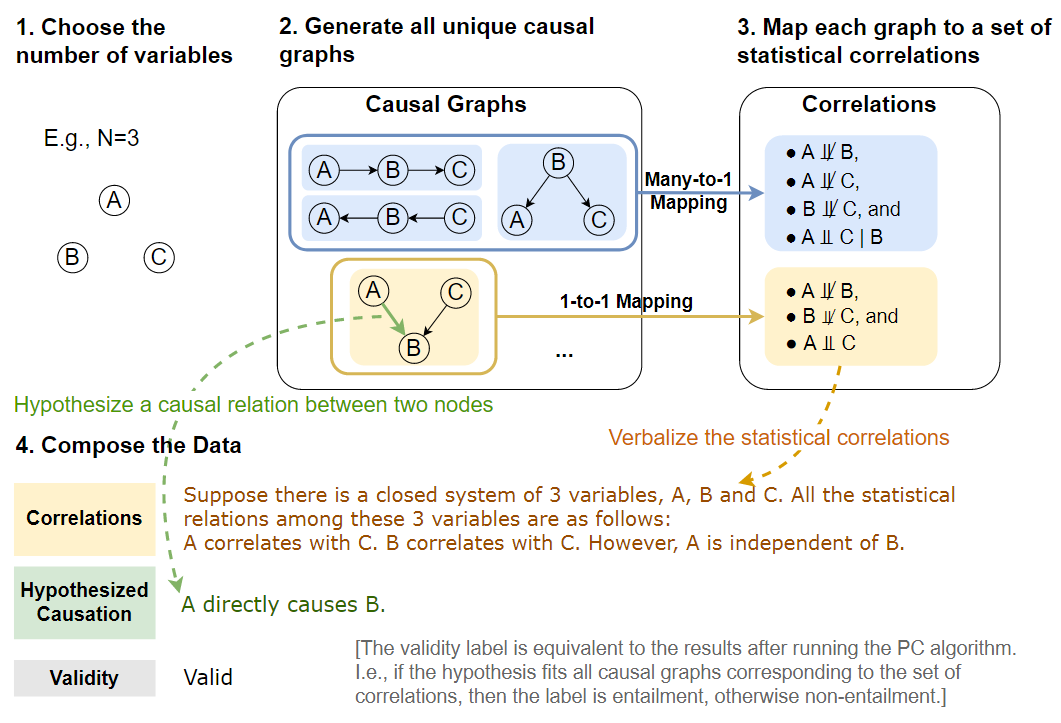
用同构检验构造图

数据生成的第一步是组成因果图，如上图的步骤1和2所示。对于一组N个变量X={X1,...,XN}，存在N(N-1)个可能的有向边，因为每个节点可以链接到除自身之外的任何节点。为了删除图中的循环，将节点按拓扑顺序排列，这只允许边Xi→ Xj，其中i＜j。通过将图的邻接矩阵限制为仅在对角线上具有非零值来实现这一点，从而产生DAG的N(N−1)/2个可能的有向边。

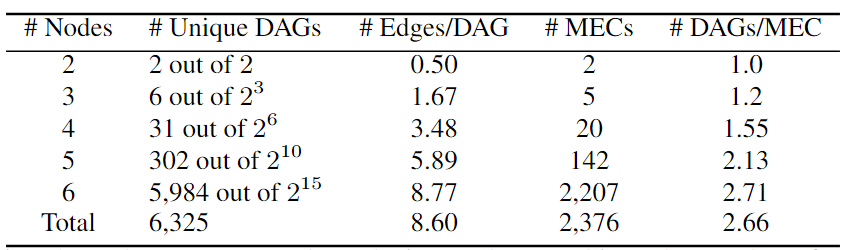
集合中可能存在同构图。为了避免这种情况，进行了图同构检查，并减少了集合，以便只保留唯一的DAG，在下表中展示了它们的统计数据。尽管其可以处理大型图，但主要关注较小的图，这些图仍然可以产生合理大小的数据集。

程序生成D-分离集

基于一组唯一的DAG，通过图论条件以编程方式生成D-分离集，如数据生成过程图的步骤3所示。对于每对节点，给定D-分离集中的变量，它们是条件独立的。如果D-分离集是空的，那么这两个节点是无条件独立的。如果不能为这两个节点找到D-分离集，那么它们是直接相关的。

组成假设和标签

在基于D-分离集生成相关性集合之后生成因果假设。对于因果关系r，重点关注两个节点之间的六种常见因果关系：是父节点、是子节点、是祖先节点(不包括父节点)、是后裔节点(不包含子节点)、混淆节点和碰撞节点。这样，假设集包含每对变量之间的所有六个有意义的因果关系，从而导致具有N个变量的图的总大小为6*N(N−1)/2=3N(N–1)个假设。

为了生成真实有效性标签，从数据生成过程图的步骤3中的相关集合开始，查找与给定相关性集合对应的相同MEC中的所有因果图，并检查假设因果关系的必要性。如果假设中提出的因果关系对MEC中的所有因果图都是有效的，那么我们生成有效性v=1;否则，v=0。

自然语言化

如数据生成过程图的最后一步所示，将上述所有信息转换为文本数据，用于CORR2CAUSE任务。对于相关语句， 将数据生成过程图步骤3中的相关性集合表示为自然语言语句s。当两个变量不能进行D-分离时，将其描述为A与B相关，因为它们直接相关并且不能独立于任何条件。如果两个变量具有有效的D-分离集C，那么将它们描述为A与给定C的B无关。在D-分离集为空的特殊情况中，A与B无关。

此外，通过将相关语句与给定变量的封闭系统的设置开始来消除歧义。最后，为了表达假设，将因果关系三元组 (Xi, r, Xj) 输入到下表中的假设模板中。

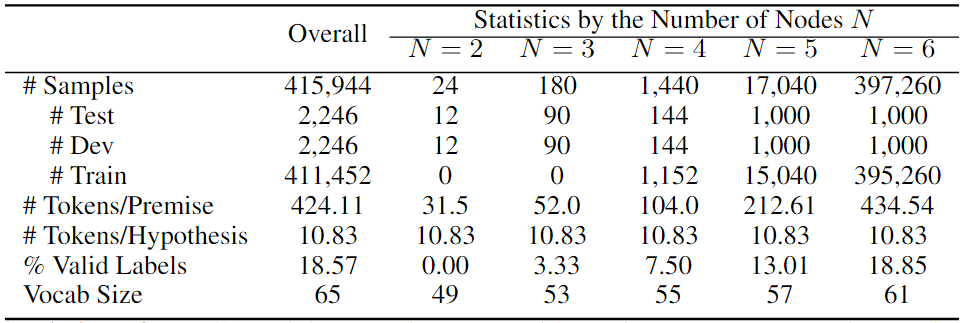
结果数据统计

CORR2COUSE数据集的统计数据，以及按子集的统计数据如下表所示。其报告了样本总数；测试、开发和训练集的拆分；每个前提和假设的token数量；隐含标签的百分比和词汇大小。

实验

实验设置

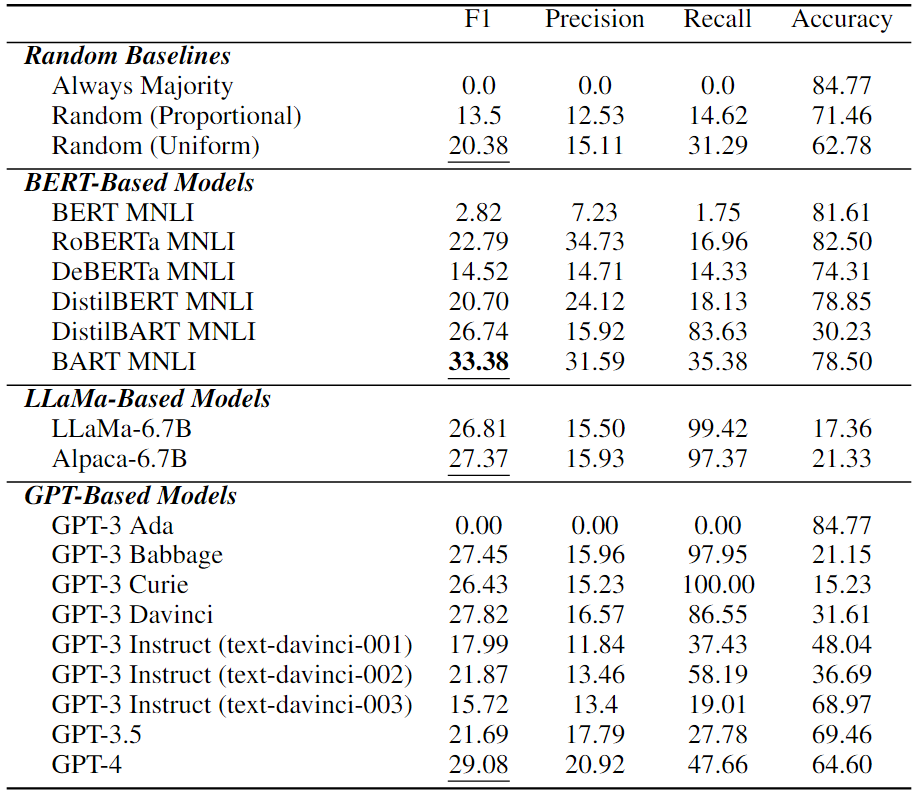
为了测试现有的LLM，首先在下载次数最多的transformers库中包括六个常用的基于BERT的NLI模型：BERT、RoBERTa、BART、DeBERTa、DistilBERT和DistilBART。除了这些基于BERT的NLI模型外，还评估了基于GPT的通用自回归LLM：GPT-3Ada、Babbage、Curie、Davinci；其指令调整版本，text-davinci-001、text-davici-002和text-davici-003；和GPT-3.5（即ChatGPT），以及最新的GPT-4，使用temperature为0的OpenAI API2,还评估了最近更有效的模型LLaMa和Alpaca,如下表所示。

现有LLM中的因果推理技能

在上表中展示了LLM的因果推理性能。可以看到，纯因果推理是所有现有LLM中一项非常具有挑战性的任务。在所有LLM中，BART MNLI的最佳性能为33.38%F1，甚至高于最新的基于GPT的模型GPT-4。值得注意的是，许多模型比随机猜测更差差，这意味着它们在纯因果推理任务中完全失败。

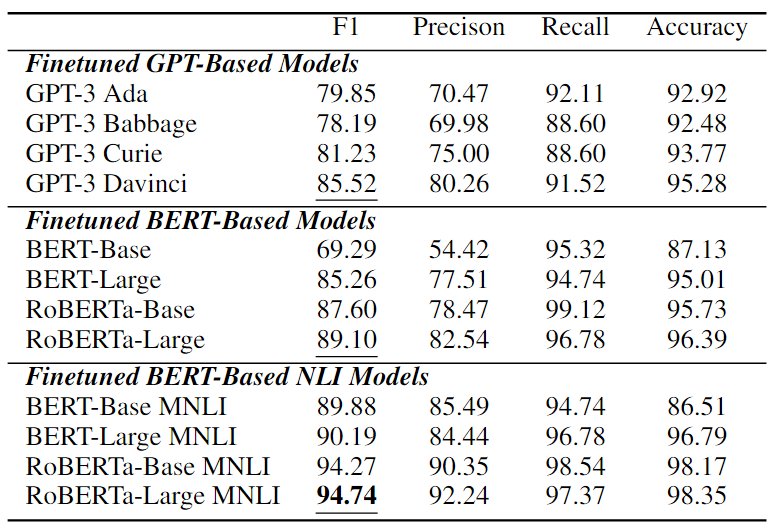
微调性能

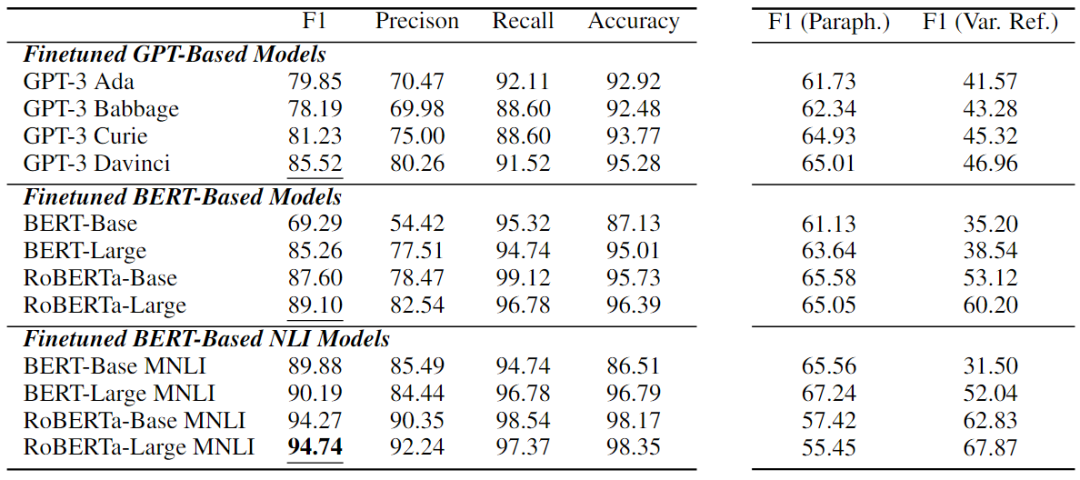
在CORR2CAUSE上微调的12个模型的展示在下表中的实验结果乍一看似乎非常强大。大多数模型性能显著增加，其中微调的基于BERT的NLI模型表现出最强的性能。性能最好的是oBERTa-Large MNLI，在这项任务中获得了 94.74%的F1值，以及较高的精度、召回率和准确度分数。

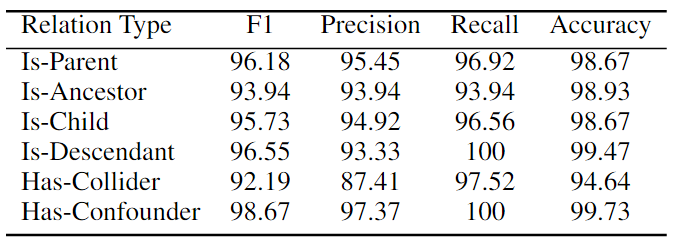
基于因果关系的细粒度性能

本文还进行了细粒度分析，通过六种因果关系类型来检验最强模型RoBERTa Large MNLI的性能。如下表所示，该模型在判断Is-Parent、Is-Descendant和Has-Confounder等关系方面非常好，所有 F1 分数都超过96%，而在HasCollider关系上则较弱。这可能是因为collider关系是最特殊的类型，需要仅基于两个变量的无条件独立性和以共同后代为条件的相关性来识别V结构。

鲁棒性分析

微调后的模型展现出了高性能，但是这些模型真的健壮地学习了因果推理技能吗?基于此本研究展开了鲁棒性分析。

两个鲁棒性测试

设计了两个简单的稳健性测试:(1)释义，(2)变量重构。对于释义，通过将每个因果关系的文本模板更改为一些语义等效的替代方案来简单地释义假设。对于(2)变量重构，颠倒变量名称的字母表，即将A, B, C翻转为Z, Y, X等。具体来说，采用了常见的文本对抗性攻击设置保留训练集并保留相同的保存模型，但在扰动测试集中运行推理。通过这种方式，将模型只过度拟合训练数据的可能性与掌握推理技能的可能性分开。

数据扰动后的结果

从下表右侧两列F1值可以看出，当解释测试集时，所有模型急剧下降多达39.29，当重新分解变量名称时，它们大幅下降高达58.38。性能最好的模型RoBERTa-Large MNLI对释义特别敏感，表明所有模型的下降幅度最大；然而，它对变量再分解最稳健，保持了67.87的高F1分数。

总结

在这项工作中，介绍了一项新任务CORR2CAUSE，用于从相关性推断因果关系，并收集了超过400K个样本的大规模数据集。在新任务上评估了大量的LLM，发现现成的LLM在此任务中表现不佳。实验表明，可以通过微调在这项任务上重新使用LLM，但未来的工作需要知道分布外的泛化问题。鉴于当前LLM的推理能力有限，以及将实际推理与训练语料库衍生知识分离的困难，必须专注于旨在准确解开和衡量两种能力的工作。
        责任编辑：彭菁