

从原理到c++代码实现 | 通过球面投影将点云转换为Range图像
描述
前言
将3维激光点云通过球面投影(Spherical Projection)转换为2维距离图像(Range Images),是自动驾驶应用场景中一种非常常见的点云处理方式。点云转换为距离图像后,通常会被输入给一个2维卷积神经网络去实现目标检测、语义分割等任务。目前采用这种点云处理方式的典型目标检测算法有RangeDet,语义分割算法有SqueezeSeg、RangeNet++、SalsaNext等。在这些文章中,都只给出一个通过球面投影转换到距离图像的最终公式,至于这个公式是怎么来的却没有详细的推导,初看论文的读者可能会比较困惑。本文将对这个投影公式做一定的推导,可能本人理解的也不是很对,欢迎大家批评指正。

球面投影推导过程
假设有一个m线的旋转扫描式激光雷达,它的垂直视场角FOV被分为上下两个部分:FOV_up和FOV_down,通常以FOV_up的数值为正数而FOV_down数值为负数,所以FOV = FOV_up + abs(FOV_down)。激光雷达旋转扫描一周得到的点云相当于是以其自身为中心的空心圆柱体,如果把这个圆柱体展开的话,那么就可以把点云投影到一个图像平面中去,这个图像平面就是距离图像。
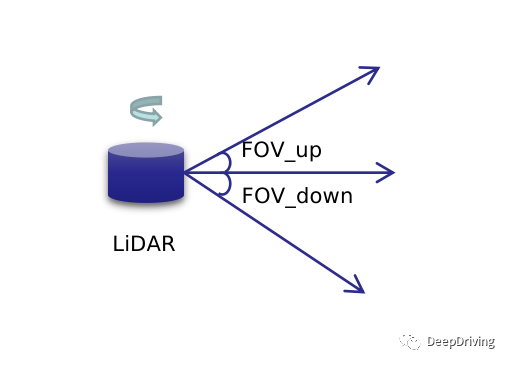
对于一个m线的激光雷达,在扫描的某一时刻会得到m个点,如果旋转一周扫描了n次,那么得到的点云就可以用一个的矩阵来表示。那么怎么把3维的点云投影到2维的距离图像平面呢?这就需要用到球面坐标。
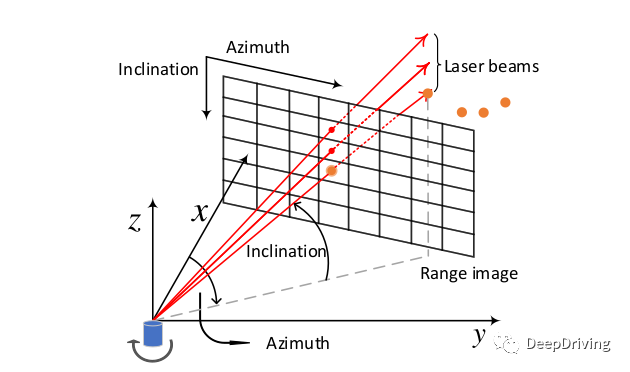
球面坐标用3个参数来表示:距离,方位角(Azimuth),天顶角(Zenith)。通常使用的激光雷达点云中的每个由3维笛卡尔坐标表示的点实际上是从球面坐标系转换而来:
让我们再通过下图来理解一下3维笛卡尔坐标系和球面坐标系之间的关系。
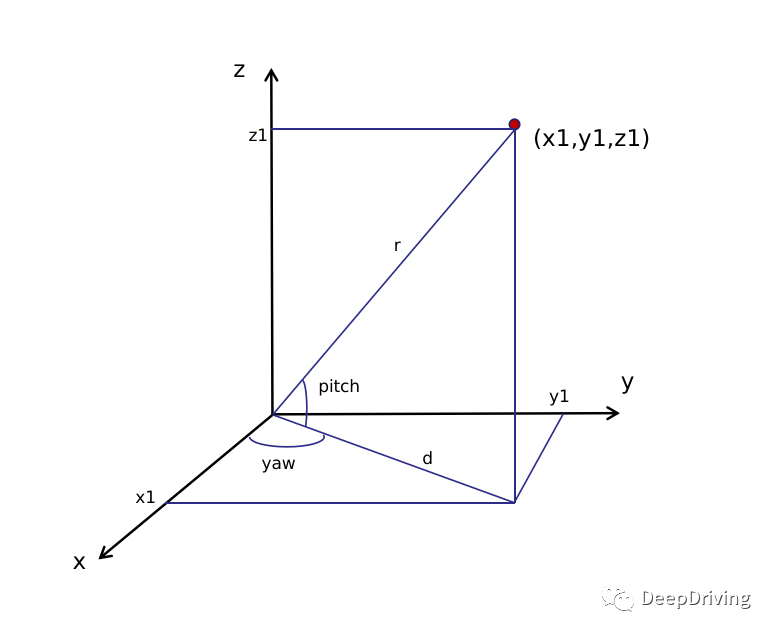
假设3维笛卡尔坐标系下的点坐标为,那么用球面坐标系可以这样表示该点:
如果以x轴方向为前视图的方向把激光雷达旋转扫描一周得到的圆柱体展开后,可以得到一副这样的图像:坐标原点在图像的中心,图像中像素的纵坐标由pitch角投影得到(范围为[FOV_down,FOV_up]),横坐标由yaw角投影得到(范围为)。
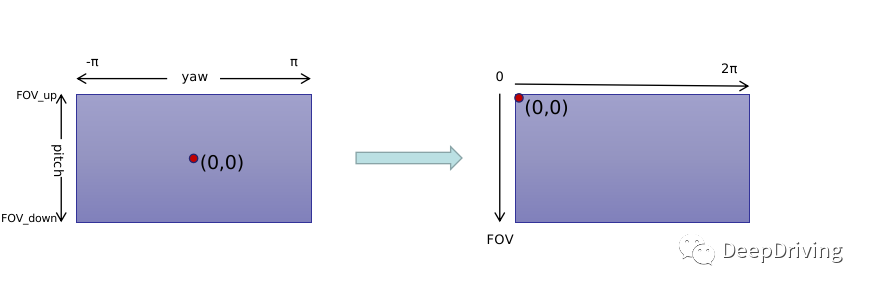
由于图像坐标系是以左上角作为坐标原点,所以上面得到的前视图还需要做一下坐标转换,把坐标原点移到左上角去:
把3维点云投影为2维图像,这种降维操作必然会带来信息损失。为了尽可能减少投影带来的信息损失,我们需要选择合适大小的投影图像。对于一个64线的激光雷达,一般会设置投影图像的高为64,那么图像的宽该如何设置呢?假设激光雷达的水平分辨率为0.35度,那么旋转一周一个激光器最多产生的点数为。在卷积神经网络中,一般会对输入特征图做多次2倍下采样,所以图像的宽度需要设置为2的次幂,这里可设置为1024。
由于不同类型激光雷达的视场角、水平分辨率不同,投影图像的尺寸也会根据需要设置为不同的值,为了适应这些变化,yaw和pitch还需要进行规范化:
规范化后,再乘以投影图像的宽高,就得到了这个点投影到距离图像的坐标:
上式中的第二步是将代入得到的。
代码实现
理解了原理后,我们再用代码来把这个投影过程实现一遍。在RangeNet++中,点云被转换为5个通道的距离图像,这5个通道分别代表点云的这5个属性。下面的代码将展示如何通过球面投影将点云转换为需要的距离图像,使用的点云数据来源于SemanticKITTI数据集。
#include
" ;
return -1;
}
const std::string pcd_file(argv[1]);
pcl::PointCloud::Ptr point_cloud(
new pcl::PointCloud) ;
if (pcl::loadPCDFile(pcd_file, *point_cloud) == -1) {
std::cout << "Couldn't read pcd file!
";
return -1;
}
constexpr int width = 2048;
constexpr int height = 64;
constexpr float fov_up = 3 * M_PI / 180.0;
constexpr float fov_down = -25 * M_PI / 180.0;
constexpr float fov = std::abs(fov_up) + std::abs(fov_down);
const std::vector<float> image_means{12.12, 10.88, 0.23, -1.04, 0.21};
const std::vector<float> image_stds{12.32, 11.47, 6.91, 0.86, 0.16};
float* range_images = new float[5 * width * height]();
for (const auto& point : point_cloud->points) {
const auto& x = point.x;
const auto& y = point.y;
const auto& z = point.z;
const auto& intensity = point.intensity;
const float range = std::sqrt(x * x + y * y + z * z);
const float yaw = -std::atan2(y, x);
const float pitch = std::asin(z / range);
float proj_x = 0.5f * (yaw / M_PI + 1.0f) * width;
float proj_y = (1.0f - (pitch + std::abs(fov_down)) / fov) * height;
proj_x = std::floor(proj_x);
proj_y = std::floor(proj_y);
const int u = std::clamp<int>(static_cast<int>(proj_x), 0, width - 1);
const int v = std::clamp<int>(static_cast<int>(proj_y), 0, height - 1);
range_images[0 * width * height + v * width + u] =
(range - image_means.at(0)) / image_stds.at(0);
range_images[1 * width * height + v * width + u] =
(x - image_means.at(1)) / image_stds.at(1);
range_images[2 * width * height + v * width + u] =
(y - image_means.at(2)) / image_stds.at(2);
range_images[3 * width * height + v * width + u] =
(z - image_means.at(3)) / image_stds.at(3);
range_images[4 * width * height + v * width + u] =
(intensity - image_means.at(4)) / image_stds.at(4);
}
// 对range通道进行可视化
cv::Mat range =
cv::Mat(height, width, CV_32FC1, static_cast<void*>(range_images));
cv::Mat normalized_range, u8_range, color_map;
cv::normalize(range, normalized_range, 255, 0, cv::NORM_MINMAX);
normalized_range.convertTo(u8_range, CV_8UC1);
cv::applyColorMap(u8_range, color_map, cv::COLORMAP_JET);
cv::imwrite("range_color_map.jpg", color_map);
cv::imshow("Range Image", color_map);
cv::waitKey(0);
delete[] range_images;
return 0;
}
对range通道可视化的结果如下图所示:

上面的代码有几个需要说明的地方:
-
fov_up,fov_down,image_means,image_stds这几个参数来源于RangeNet++预训练模型中的arch_cfg.yaml文件。 -
std::clamp需要c++17支持,编译的时候请使用-std=c++17编译选项。 -
实际使用中
width * height的值只需要计算一次,没必要在循环里面反复计算,这里这么写只是为了方便理解。
参考资料
-
RangeDet: In Defense of Range View for LiDAR-based 3D Object Detection -
https://towardsdatascience.com/spherical-projection-for-point-clouds-56a2fc258e6c
-
阿里云SDK再升级,宣布支持C++语言2018-02-08 0
-
如何将二维数组转换为图像2013-03-10 0
-
【创龙TMS320C665x申请】图像中数字及字母的识别2016-03-04 0
-
基于FPGA水平垂直投影(字符分割)法的实现2018-08-07 0
-
基于Verilog的垂直投影实现2019-03-03 0
-
如何将ADC代码转换为电压2019-07-23 0
-
如何利用coder将matlab中的程序转换成C/C++2021-08-17 0
-
如何在新版本中将C项目转换为C++呢?2023-01-06 0
-
将ONNX模型转换为中间表示(IR)后,精度下降了怎么解决?2023-08-15 0
-
人脸识别C/C++源代码2010-02-09 1320
-
将代码转换为电压,如何可以实现?2017-10-12 11500
-
关于彩色图像高斯反向投影基于OpenCV的C++代码2022-05-31 973
-
通过将异步获取的图像与LiDAR点云对准的方案2023-12-12 806
-
C++在Linux内核开发中从争议到成熟2024-01-31 650
-
OpenCV图像识别C++代码2024-07-16 2130
全部0条评论

快来发表一下你的评论吧 !

