

自动驾驶汽车规避转向的模型预测控制
电子说
描述
层输出的参考轨迹,结合车辆自身状态,控制车辆跟踪参考轨迹形式,实现车辆的纵、侧向控制。车辆的纵向控制主要实现速度的跟踪,侧向控制则实现路径的跟踪。近年来,基于车辆运动学与动力学模型的模型预测控制(MPC)理论在自动驾驶车辆控制方面得到了广泛的应用,MPC基于预先设定的系统模型,通过滚动优化,解决设定的优化问题并求解出控制输入。MPC的优点在于能够系统地处理输入和输出的约束,适用于多输入多输出控制系统,同时可以明确地考虑系统的时间延迟。
摘要:模型预测控制(MPC)常用于自动驾驶汽车的转向控制,通常选择简单的车辆动力学模型作为参考模型。然而简单的车辆动力学模型不足以用于需要较快转向操作的规避转向控制。本研究的目的是设计一种适用于规避转向控制的MPC。在MPC设计过程中考虑了转向系统模型和车辆模型。所提出的转向模型在保持简单结构的同时,还能够有关扰动、执行器带宽和电机电压的信息。控制器以跟踪误差为代价,计算得到不违反电压约束的要求较低期望转向角。否则,电压饱和时MPC将导致期望的规避转向操作失败,从而无法跟踪转向角。仿真和实验结果表明,所设计的转向控制器在允许的电压范围内成功地完成了了规避转向操作,并且其性能优于基于简单车辆模型的常规MPC控制器。
1引言
模型预测控制(MPC)是一种基于模型的控制方法,用于在满足多个约束的同时控制动态系统。MPC中使用的模型表示系统的动力学特性。该模型能够预测由控制变量的变化引起的系统状态的变化。优化器会确定一系列优化控制变量,这些变量在能够在满足约束的前提下最小化成本函数值。MPC中使用的模型通常很简单,并且出于减少计算量的考虑,常采用线性形式表示模型。通过当前状态测量的反馈,可以减弱模型误差所造成的影响(García等,1989)。
由于MPC能够明确考虑约束条件和次优性能(Falcone等,2007a,2007b,2007c; Shim等,2012),因此常使用MPC设计自动驾驶汽车的转向控制器。这些MPC中的模型大多基于车辆动力学模型,而没有考虑执行器的动力学特性。MPC的控制输出不是执行器层的信号(电压、电流等),而是高层级的信号(转向角、制动力等)。实际上,这类控制器的设计是在执行器控制器具有完美跟踪能力的前提下进行的(Kim等人,2014)。
针对大多数的驾驶员操纵,例如以规则速度行驶的车道变更和转弯操纵,不考虑执行器模型的控制器可以满足其控制精度,因为执行器的带宽足以覆盖常规操作所需的动作频率。然而,在某些操纵中,例如需要非常快速的转向动作的规避转向操纵(Keller等,2014),仅有简单的车辆动力学模型是不够的。在这种情况下,通常在常规操作中可忽略的模型误差或模型的缺失引起的影响将变得十分显著,或者如果在模型中未适当考虑扰动,扰动的数值将会过大,并导致对于扰动的抑制不足。
这项研究的目的是为转向控制器设计一种适用于规避转向操纵的MPC。为此,我们需要在MPC设计中同时考虑转向系统模型与车辆模型。该模型应提供有关不不可忽视干扰的信息,并通过监视执行器的性能极限来考虑执行器带宽。但是,为了保持较低的计算负荷,应使结构尽可能的简单。
2研究问题描述
为了代替人类驾驶员,配备有自动转向系统的自动驾驶汽车需要具备决策、控制、执行等方面的自动功能。在自动驾驶汽车中,转向系统负责执行转向操作。图1显示了自动转向控制功能的常用框架(Kim和Song,2002年)。在高层级控制器中确定所需的转向角,由电机控制器或ECU调节电机电流以跟踪所需的转向角。
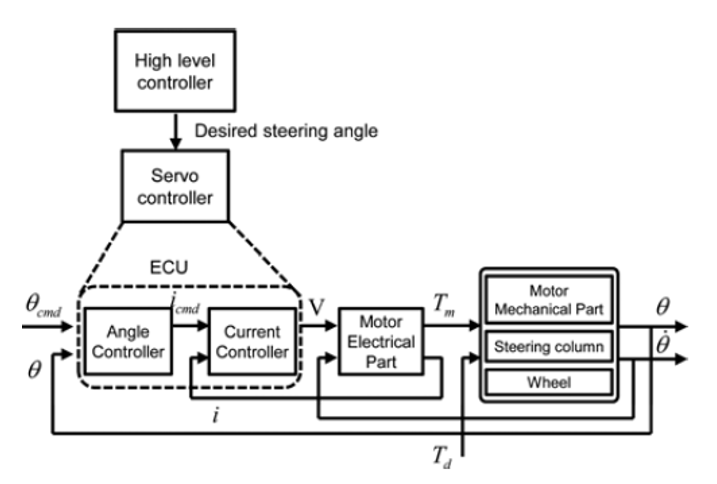
图1 转向系统功能配置
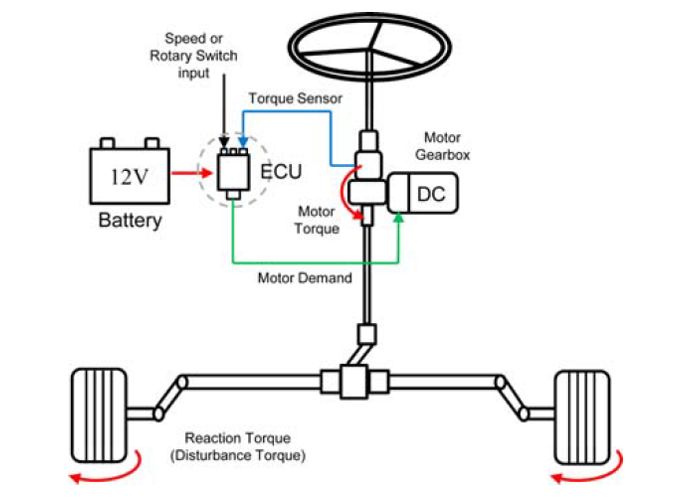
图2 电动助力转向(EPS)系统结构
目标改造车辆选择簧载质量为1370kg的常规D级轿车,例如Audi A4、BMW 3系列等。如图2所示,自动驾驶汽车中最常见的转向系统是电动助力转向系统(EPS)。EPS中的ECU提供了伺服控制,以在内外扰动下跟踪目标转向角。在ECU中设置了两个伺服控制器,分别为用于计算目标电流的转向角控制器、用于计算目标电压的电流控制器(Wei等人,2010)。两个控制器的控制分别来自于转向系统的机械惯性与轮胎的扰动转矩、电机线圈的电感与反电动势等。
对于转向系统而言,其能提供的最大角速度和最大角加速度取决于电机的最大扭矩和车辆操纵过程中来自轮胎的干扰扭矩。电机转矩与提供的电流成正比,而电流被电压限制动态饱和,对于常见的乘用车,该电压限制为12 V(Saifia等,2015)。来自轮胎的干扰扭矩则源自横向车辆操纵期间的轮胎侧向力,与轮胎侧偏角成函数关系。
如图3(a)所示,当典型的换道操作所需的转向角适中时,由于系统惯性而存在一些相位滞后,但角度控制器和电流控制器的跟踪性能也是可以接受的,也并未发生电压饱和问题(Li等; 2011;Yoshida等,2008; Zaremba等,1998)。
但在转向要求过高时,即使轮胎滑移角处于很小的范围之内,也会出现违反电压饱和限制的情况。如图3(b)所示,当车辆执行规避转向操作时,转向角速度与角加速度远高于图3(a)中操作对应的数值。可以看到,高层控制器仍能够计算得到适当的目标转向角,但伺服控制器无法对其进行跟踪。可能的原因包括:
(1) 转向角变化的更快,使得系统惯性引起的相位滞后不可忽略;
(2) 规避转向操作时的扰动转矩远高于典型换道操作时的扰动转矩;
(3) 对应目标转角的期望电压值高于12V,相位滞后的值无法通过12V电压得到充分的补偿。
因此在确定高层控制器以及参考模型时,应考虑上述三个因素。
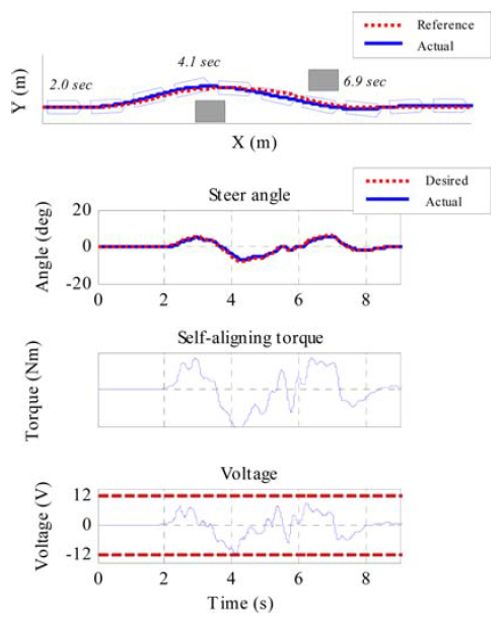
(a)
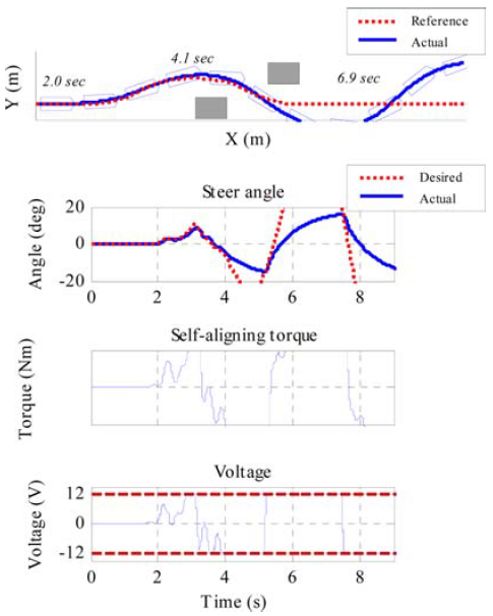
(b) 图3 常规转向与规避转向工况下的跟踪与控制情况
3控制系统建模
控制系统建模包括车辆模型、转向系统模型、扰动模型、电压模型。 车辆模型采用道路跟随模型,该模型基于二自由度自行车模型,增加了车辆相对于目标轨迹的侧向位移、航向角误差这两个附加状态(Ulsoy等,2012),可表示为:
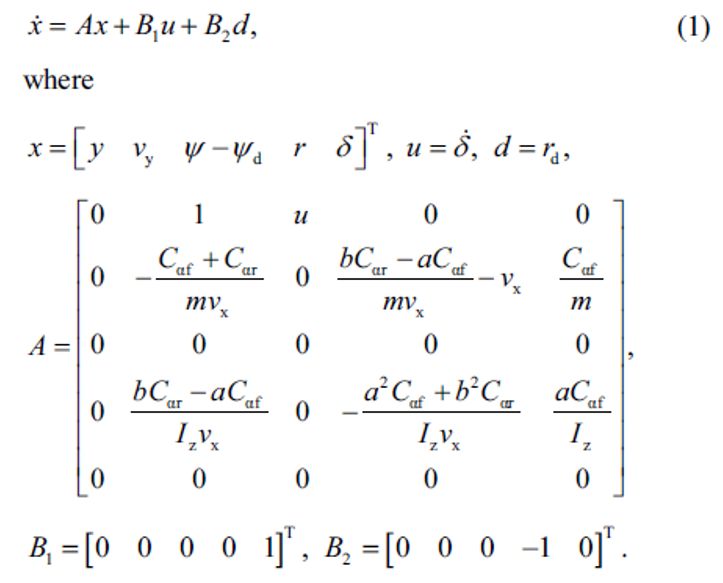
系统的输入量为方向盘转角的角速度,扰动量为由目标轨迹确定的期望横摆角速度。输入量选择转角的角速度,是为了防止MPC方程中方向盘转角噪声过大。
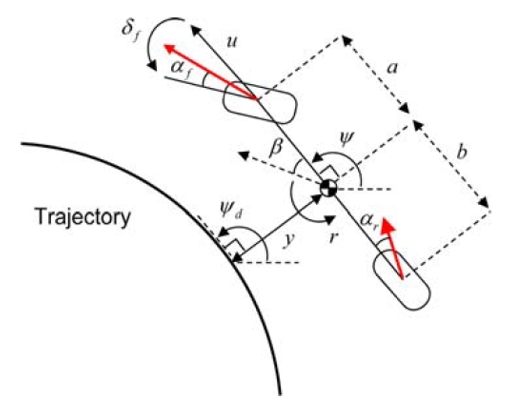
图4 道路跟随车辆模型
转向系统由许多子系统构成,直接建模得到的模型复杂度很高,且对于控制器设计而言高逼真的转向系统模型是不必要的。因此可采用相对简单的二阶线性模型描述转向系统:
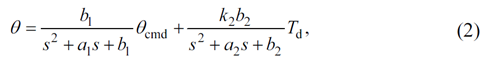
该系统有两个输入:ECU的控制输入与轮胎的扰动转矩。由于电气部分与ECU部分的动态特性快于机械部分,因此可以将上式简化为:
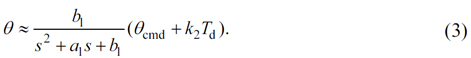
在双移线工况下将上述简化后的转向系统模型与原始系统进行比较,如图5所示,简化后的系统仍具有有意义的物理状态,且能够较容易的获得对应的状态空间形式。
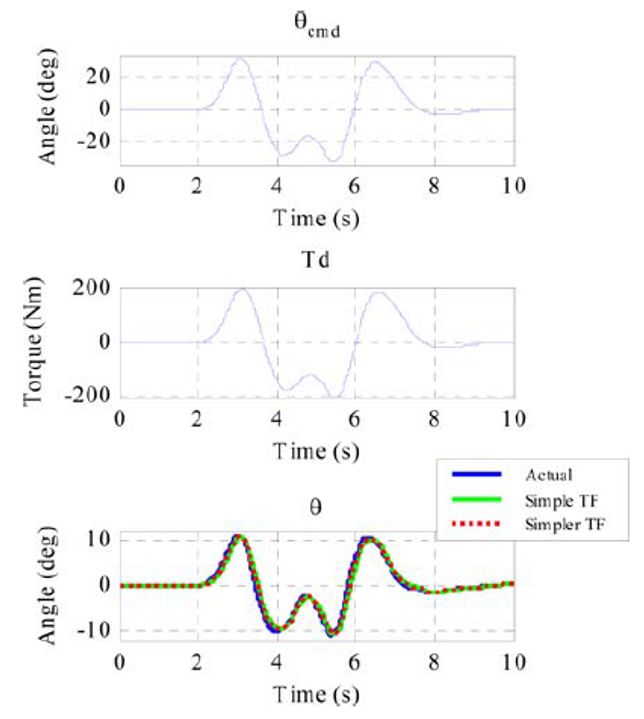
图5 使用双移线操作进行转向系统模型识别的结果
扰动模型指轮胎的扰动转矩模型。轮胎的扰动转矩与轮胎的侧向力有关,而轮胎的侧向力与轮胎滑移角有关。滑移角较小时,侧向力与滑移角呈线性关系;滑移角较大时,该关系变为非线性。假设该线性关系可表示为:
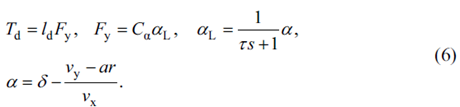
本文中提到的扰动模型是在小轮胎滑移角的前提下建立的,假设关系线性的有效范围为-4°~4°。 上述的三个模型均未包含任何有关电机电压信息的状态、输出量等,如果将电压信息添加到上述模型中,模型的规模与复杂程度将增加,并影响MPC的实际控制效果。因此本文针对电机电压建立了专门的电压模型,构建电压与转向角之间的函数关系,使用转向系统的状态与传递函数计算得到电机电压的值。使用与前述类似的简化方法,构建模型为:
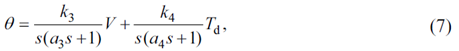
将扰动模型与转向模型表示的车辆状态代入,可得到:
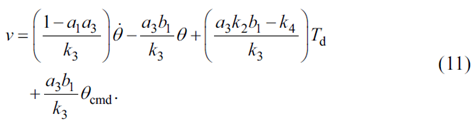
4控制器的设计
在III中,我们得到了MPC中将要使用到的模型,包括5状态的车辆模型、3状态的转向系统模型、1状态的扰动模型、0状态的电机电压模型,模型的总状态数为9。 为了减少计算量,将模型分别放入两个MPC结构之中,如图6所示,一个为车辆模型MPC,另一个为转向系统模型MPC,使得9个状态的优化问题转换为两个具有5个状态、3个状态的小型优化问题的组合,减少了计算量。扰动模型位于MPC结构的外部。而电压模型包含在两个MPC模块中,使得这两个模块确定的指令角度都不会使得电压超过饱和限值。由于电压模型是状态的代数方程,因此电压模型的引入不会增加MPC方程的维数,即不增加方程的复杂程度。
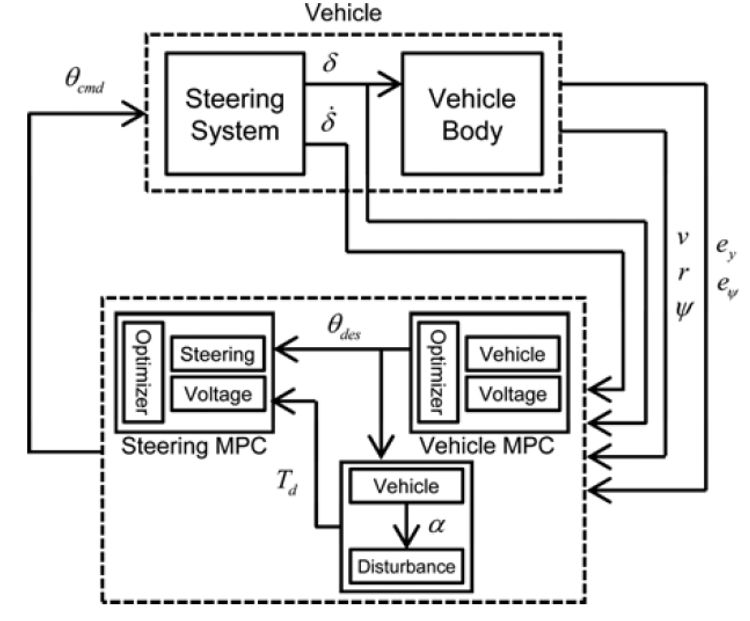
图6 转向系统与控制系统结构
该MPC中的优化问题由具有线性约束的线性系统表示,因此可转换为典型的二次规划问题。对于式(14)表示的离散系统,可给出对应的成本函数为式(14)

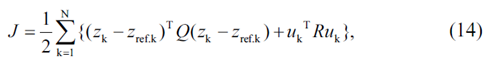
也可以给出系统的输出约束与输入约束如下:

 该部分的完整解释详见Son et al.,2017。 对于车辆模型MPC,在使用线性MPC的设计综合时,需要选择系统的输出、约束以及加权矩阵的值。基于车辆模型MPC的目标是使得车辆相对于参考路径的侧向位移与航向角误差最小,同时将轮胎滑移角、转向角、电压等保持在相应的极限范围内(式19)。
该部分的完整解释详见Son et al.,2017。 对于车辆模型MPC,在使用线性MPC的设计综合时,需要选择系统的输出、约束以及加权矩阵的值。基于车辆模型MPC的目标是使得车辆相对于参考路径的侧向位移与航向角误差最小,同时将轮胎滑移角、转向角、电压等保持在相应的极限范围内(式19)。
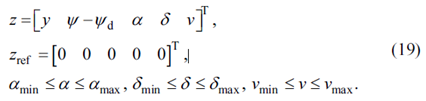
矩阵R被设计为非负标量,矩阵Q被设计为式(20)所示的形式,原因是我们只希望对相对侧向位移与相对航向角误差进行惩罚,因此在对角线上仅有第一与第二个元素为非零。

对于转向系统模型MPC,其目标是最小化方向盘转角的跟踪误差,同时将电压保持在极限范围以内。
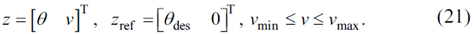 矩阵R被设计为非负标量,矩阵Q被设计为式(22)所示的形式,理由与车辆模型MPC中的矩阵Q类似。指令角度相对于时间的导数受到R的惩罚,从而抑制了指令角度的过大噪声。
矩阵R被设计为非负标量,矩阵Q被设计为式(22)所示的形式,理由与车辆模型MPC中的矩阵Q类似。指令角度相对于时间的导数受到R的惩罚,从而抑制了指令角度的过大噪声。

5仿真与实验验证
为了验证本文所提出的用于规避转向条件下跟踪控制的MPC,我们对其进行了仿真与实验测试。为了进行比较,我们设计了两个基于MPC的控制器,一个为仅基于车辆模型的常规MPC,另一个为基于车辆模型与转向系统模型的改进MPC。
使用CarSim对进行仿真验证,仿真车速为30km/h。图7(a)、图7(b)分别为常规MPC与改进MPC在规避转向操作下的仿真结果。可以看到,常规MPC可以计算出适当的期望转向角,但由于电压饱和,伺服控制器无法跟踪期望转向角。而改进MPC在考虑扰动与电压限制的情况下计算出了相应的期望转向角,使得伺服控制器能够成功对其实现跟踪。仿真结果表明,额外考虑转向系统模型的MPC具有比常规MPC更加精确的实际系统模型,并能够有效处理系统约束问题。
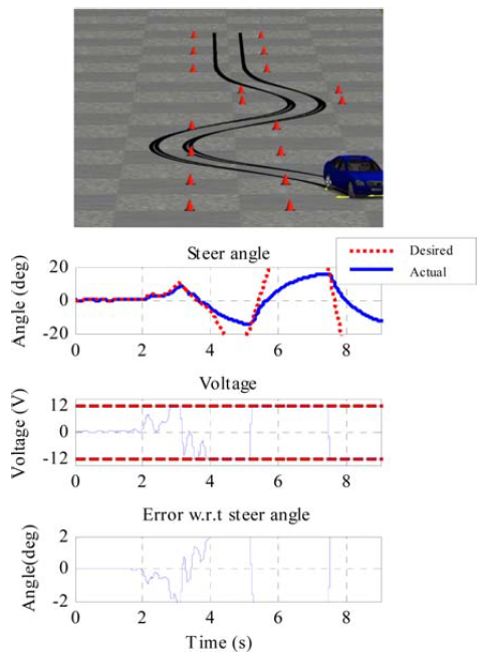
(a)
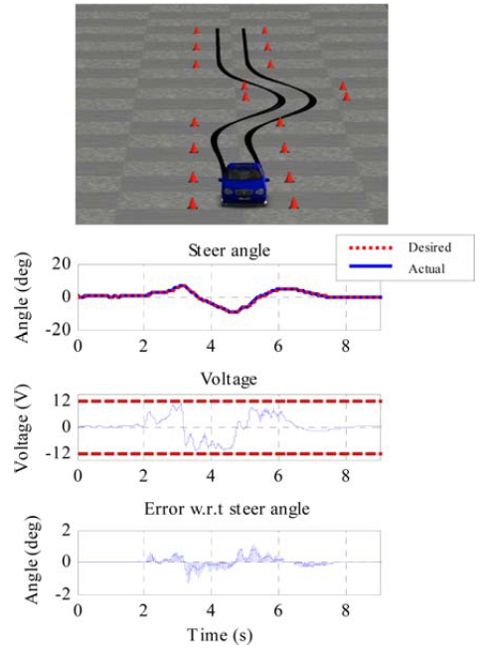
(b) 图7 不同MPC在规避转向操纵下的仿真表现
除了仿真验证,还进行了相应的实验验证。如图8所示,实验系统由标定车辆、摄像头、快速控制原型系统dSPACE等组成。对称布置的标记器附着在车辆的顶部,标记器跟踪算法提供了车辆的位置与航向角;摄像头获取的车辆信息与车辆的传感器信号则通过无线通信传输到dSPACE中。实验结果如图9(a)、图9(b)所示,实验中的标定车速为0.2m/s。可以看到,常规MPC为车辆提供了计算得到的期望转向角,但违反了电压限制,因此车辆无法遵循所需的路径行驶。而改进MPC控制的车辆在允许的电压范围内成功地跟踪了所需路径。试验结果表明,按照该比例缩放并标定的车辆,其转向系统的物理极限与电压约束得到了明确的处理,并验证了改进MPC的次优性能。
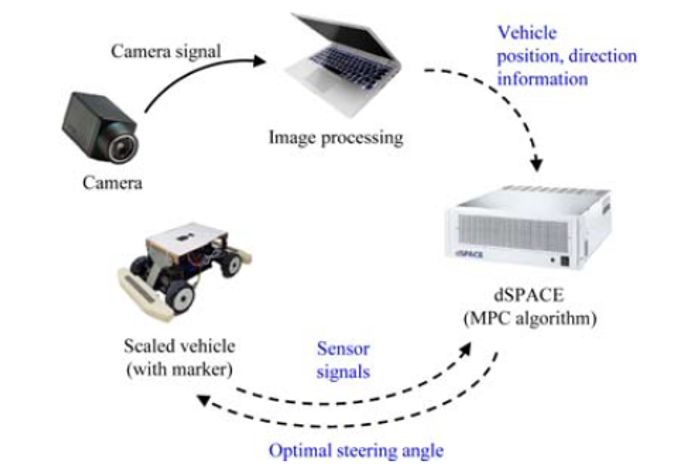
图8实验系统结构
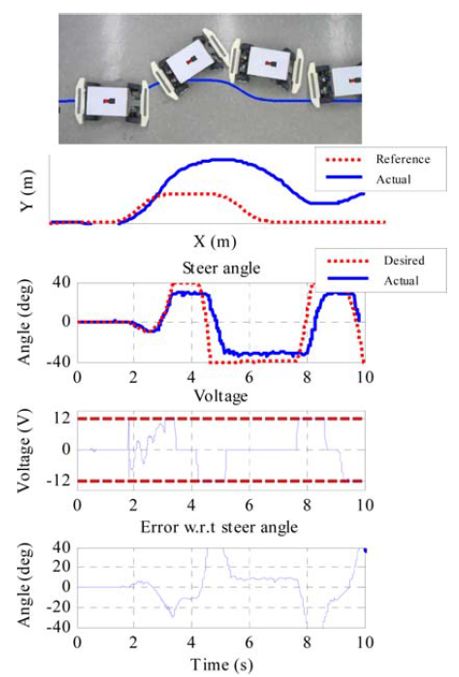
(a)
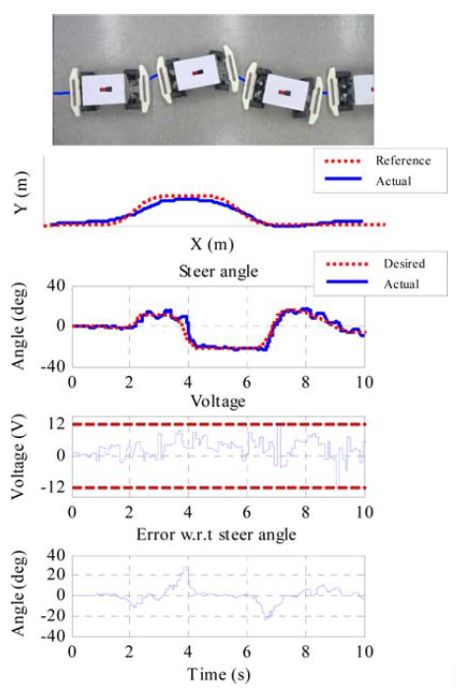
(b)
图8 不同MPC在规避转向操纵下的实验表现
6结论
本文设计了一种用于自动驾驶汽车转向控制器的MPC,该MPC适用于转向操纵中的规避转向操纵。规避转向操纵需要进行非常快速的转向操作,而仅依靠简单的车辆动力学构建参考模型是不够的。因此,本文在MPC设计中同时考虑了转向系统模型与车辆模型。
本文对转向系统进行了建模,该模型可以在保持简单结构以减少计算负荷的同时,提供有关扰动、系统带宽和电压状态的信息。仿真和实验结果表明,在允许的电压范围内,该控制器能够很好地完成跟踪任务,并且在规避转向操作期间的表现优于仅基于车辆模型的常规MPC。
文章来源:汽车自动驾驶技术
审核编辑:汤梓红
-
FPGA在自动驾驶领域有哪些应用?2024-07-29 0
-
谷歌的自动驾驶汽车是酱紫实现的吗?2011-06-14 0
-
汽车自动驾驶技术2016-04-14 0
-
自动驾驶的到来2017-06-08 0
-
AI/自动驾驶领域的巅峰会议—国际AI自动驾驶高峰william hill官网2017-09-13 0
-
高级安全驾驶员辅助系统助力自动驾驶2018-09-14 0
-
如何让自动驾驶更加安全?2019-05-13 0
-
自动驾驶汽车的处理能力怎么样?2019-08-07 0
-
自动驾驶系列报告大放送了涉及传感器,芯片,执行控制等2019-08-09 0
-
模型预测控制+逻辑控制2021-08-17 0
-
模型预测控制介绍2021-08-18 0
-
自动驾驶技术的实现2021-09-03 0
-
自动驾驶线控底盘VCU功能介绍2021-09-07 0
-
什么是MPC模型预测控制?2021-11-22 0
-
无人驾驶汽车模型预测控制相关源代码2021-03-12 963
全部0条评论

快来发表一下你的评论吧 !

