基于一种用于JumpStarter的抗离群的采样算法

 

随着在线服务系统的蓬勃发展，多元时间序列的异常检测，例如CPU利用率的组合，平均响应时间和每秒请求，对于系统可靠性很重要。尽管为此目的设计了一系列基于学习的方法，但实证研究表明，这些方法遭受了长时间的初始化时间，以获得足够的培训数据。本文压缩感测技术引入了多元时间序列异常检测，以快速初始化。为了构建跳跃异常检测器，提出了一种名为Jumpstarter的方法。基于域特异性见解，设计了一种基于形状的聚类算法以及一种用于JumpStarter的抗离群的采样算法。

背景及动机

1、多元时间序列

在在线服务系统中，操作员不断收集多个指标的监视数据，或从日志中提取数值。服务水平度量（例如，平均响应时间）或机器级度量（例如CPU利用率，内存利用率）通常是通过相等的间隔收集的，形成单变量时间序列。但是，任何单变量时间序列都无法捕获系统的所有类型的性能问题。由于系统通常具有监视指标的集合，因此可以表示为多变量时间序列，其中包括各种类型的单变量时间序列，从而跟踪性能问题的各个方面。随着系统的规模和复杂性的增加，手动检查系统异常变得越来越困难。因此，多元时间序列异常检测非常重要。

2、异常检测

使用多元时间序列的异常检测在线服务系统中很重要。在以前的异常检测工作中，操作员在以下几点上有一个粗略的共识：

1）多元时间序列异常是数据点或数据段，它显着偏离了操作员对操作员的期望正常行为，可以在视觉上观察到。

2）异常表明可能出现问题，尽管仍需要进一步调查进行验证。

3）异常检测通常用作失败发现机制。

初始化时间的实证研究

1、异常检测初始化时间

在部署或更新的新服务时，运营商通常为其启动一种异常检测方法。如图所示，异常检测方法的初始化时间是启动何时（T1）到有效的时间（T2）。

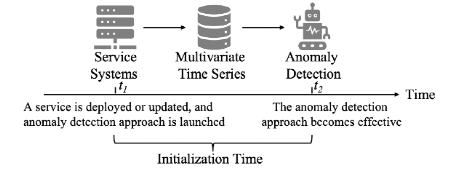
许多先前方法使用基于学习的工作流来检测异常。通常，它们是根据历史数据进行定期培训的。这些方法的初始化时间，例如数十天相对较长，因为它们通常需要提供大量的历史数据进行培训。在表中，列出了不同数据集上五种基于学习的异常检测方法的建议初始化时间。

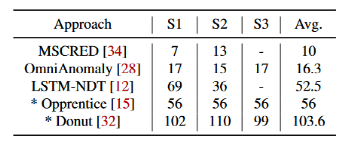
2、增量再训练

考虑到基于学习的异常检测方法的漫长初始化时间，人们可能建议逐步保留，即逐渐（逐步）添加一个短期（例如一天）数据来训练这些方法。这样，我们可以逐步提高这些方法的性能。每次添加一天的数据是因为这些基于学习的方法至少需要数千个数据点来收敛。然后，尝试将增量再培训应用于最新的多元时间序列检测方法，即全曲率和mecred。

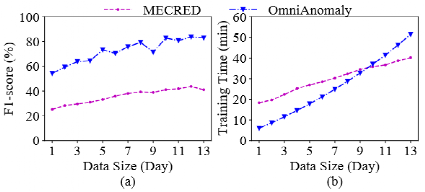
这听起来很理想，但是使用增量再培训的异常检测不能确保令人满意的性能。图中显示了随着训练数据的增加（日复一日）的增加，F1的平均得分和训练时间。从图中，可以看到，使用更多的训练数据，以及使用更多的训练数据，直到将10天的数据用于培训，它们才收敛。一个主要原因是，这些基于学习的方法必须从大量培训数据中明确学习多元时间序列的概率分布，以捕获其正常行为。图中表明，训练时间随训练数据的规模线性增加。当培训数据集包含10天的数据时，大约需要35分钟才能训练。因此，这些方法由于其非舒适性和相当大的培训成本而不适合新部署或更新的系统。

Jumpstarter方法

1、关键思想和挑战

为了处理上述基于学习方法的局限性，将压缩感测（CS）用于多变量时间序列异常检测。CS是一种信号处理技术，用于从一系列采样测量结果中重建信号。从这些样品中重建的信号保留了原始信号的高能量成分，在某些轻度假设下概率很高。可以通过检查重建信号是否与原始信号（多元时间序列）存在超过白噪声的不同，来确认检测异常。由于CS不需要任何训练，因此基于CS的异常检测的初始化时间是窗口大小W。

有两个方式来进行信号重建：

1、将多变量时间序列视为一个N×W的矩阵。

2、将多变量时间序列视为N个长度为W的单变量序列。

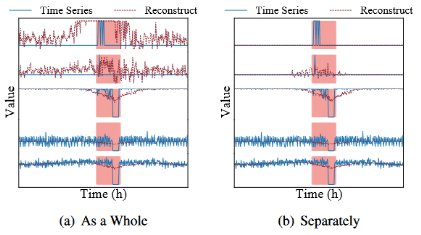
结果如图所示，第一种方式，对数据随机采样并进行重建之后，出现前两维数据在全时间跨度内重建序列和原始序列都差异较大的情况。

第二种方式，原始和重建的单变量时间序列之间的差异表现为正常段中的白噪声和异常的大波动，可准确捕获每个单变量时间序列的异常。但是，它无法捕获多元时间序列之间的复杂关系。此外，由于大量单变量时间序列的挑战，单独的重建在计算上更昂贵。

2、概述

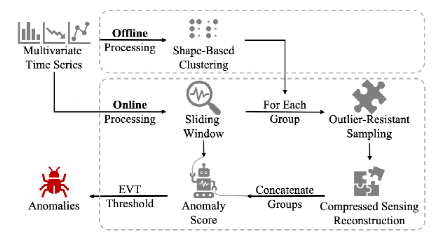
1、采用一种基于形状的聚类方法将多元时间序列的单变量时间序列分组为离线处理中的几个组。

2、滑动窗口技术应用于在线异常检测中的多元时间序列。

3、对于每组单变量时间序列，使用一种新型的抗异常值采样算法来解决来自异常段采样引入的挑战，并应用压缩感测来重建它们。之后，比较原始时间序列和重建的多元时间序列，并使用EVT阈值对异常得分进行异常确定。

3、Shape-Based Clustering

先前提到的两种方式都存在自己的问题。特别是第一种方式无法很好的在不同形状的维度上进行重建，因此一种方式就是按照形状将多元分为几个群集进而重建每个群集。

采用基于形状的距离（已有相关工作），是一种基于跨相关的方法，以测量两个单变量时间序列之间的距离。在处理高维度序列时，它可以实现高计算效率。表中说明了聚类结果的示例。多元时间序列的九个单变量时间序列分为三个群集。在每个集群中，时间序列与其相应监视指标的物理含义相关，表明这个方法是直观有效的。

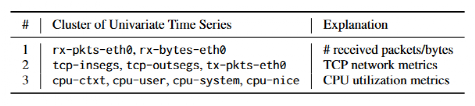
       基于一日数据的每个多变量时间序列将单变量时间序列集成，因为大多数单变量时间序列大致与24小时的周期大致相同，与客户的企业使用模式相吻合。此外，在软件更改后，单变量时间序列的形状通常保持不变。因此，在软件更改后，它无需重新群集。

4、Outlier-Resistant Sampling

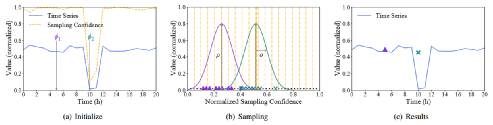
异常通常是观察窗口（滑动）窗口中的异常值。如果异常的持续时间比窗口大小更长，则可以从一开始就捕获，因为它与正常模式显着不同。因此，可以采用简单的离群检测算法来获得每个数据点的采样置信度。数据点可能越高，其采样置信度越低，选择的可能性就越小。基于这种见解，文章设计了一种抗离群的抽样算法，即一维随机高斯，它不仅可以保证撕裂，而且还可以抵抗异常值。

从图中的result部分可以看出最后得到的两个样本点，尽管绿色的取样点位于原始时间序列的异常段，但是得到的样本点依旧稳定。

4、Compressed Sensing Reconstruction

压缩传感理论首先将信号投影到一个低维的信号空间,然后通过解一个基于凸优化的非线性恢复算法将信号恢复,而仅仅需要很少的数据，文章使用了CVXPY这个凸优化算法。

5、异常得分

使用欧几里得距离计算两个时间序列之间的差异得分。

6、选择阈值

要正确生成异常警报，需要准确选择一个阈值，以确定异常得分是否足够高以触发警报。静态阈值无法正常工作，因为数据分布会随时间变化。由于JumpStarter产生的异常得分的极值通常代表异常，因此采用广泛使用的极值理论（EVT）自动调整异常阈值。EVT是一种旨在找到极值定律的统计理论，并且不假定数据分布。已证明它可以准确选择异常检测方法的阈值。

实验

实验部分主要解决以下研究问题：RQ1：Jumpstarter在多元时间序列序列检测中的表现如何？RQ2：每个组件是否有助于Jumpstarter？RQ3：Jumpstarter的主要参数如何影响其性能？数据集的情况如下图所示。

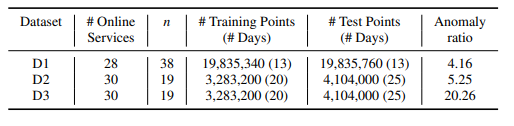
RQ1: Performance of JumpStarter

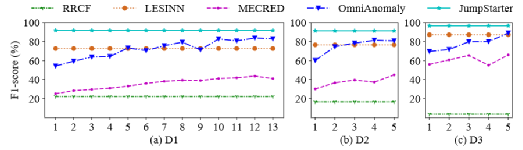
可以看到，在在线实验中，JumpStarter的性能明显优于所有三个数据集中所有段的四个基线方法。

接下来是软件更改后的异常检测。

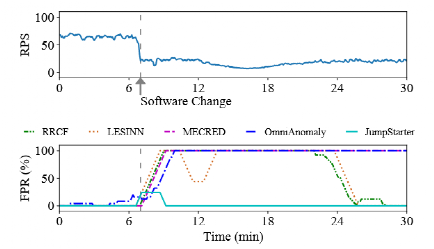
上图显示了软件更改后五种方法的平均FPR，所有这些方法遇到的软件更改都发生在图中的第七分钟。可以观察到，在这些软件更改后，所有五种方法都会产生误报。但是，JumpStarter仅遭受大约五分钟的高FPR，此后其FPR变得很低。

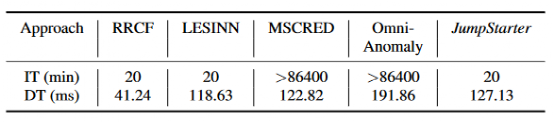
同时可以看到JumpStarter的准备时间和运行时间都比较少。

RQ2: Contributions of Components

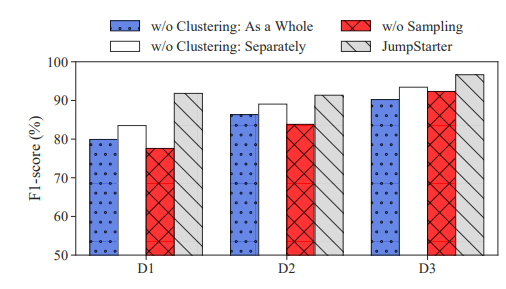
通过去除各个步骤得到的F1-score来看，基于形状的聚类和抗异常值的采样的组合有助于准确有效。

RQ3: Parameter Sensitivity

JumpStarter的初始化时间取决于检测窗口大小w。我们从经验上将窗户尺寸从十分钟增加到60分钟。图中显示了随着窗口尺寸的增加，Jumpstarter的平均最佳F1分数和连杆检测时间如何变化。在窗口大小达到20分钟之前，Jumpstarter的准确性会增加，之后它变得稳定，而检测时间逐渐增加。因此，窗口尺寸为二十分钟，这使Jumpstarter既准确又有效。请注意，对于那些持续超过20分钟的异常，Jumpstarter仍然能够检测到它们，因为它可以在启动时很容易捕获这些异常。

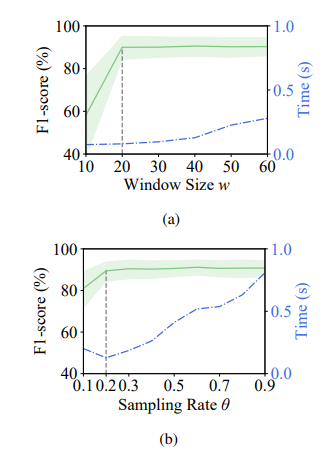
JumpStarter的另一个重要参数是初始采样率σ。图中显示了f1的平均最佳F1分数和跳跃体的点检测时间如何随着σ的增加而变化。同样，当采样率从0.1增加到0.2时，JumpStarter的F1得分会增加，此后变得稳定。