模拟信号和数字信号的桥梁——奈奎斯特采样定理

在我们周围有着各种各样的模拟信号，比如，电流，电磁波，温度，声音等等。作为计算机系统来说，它只认识0和1，意味着它只能处理数字信息，但是，它是如何处理我们周围的这些模拟信号的呢？要理解这个问题，我们需要理解在数字信号处理领域中一个非常重要的定理——采样定理，它是模拟信号数字信号之间的一个基本桥梁，本文将和大家一起学习奈奎斯特-香农采样定理。

采样定理1928年由美国电信工程师奈奎斯特首先提出来的，因此称为奈奎斯特采样定理。1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理。1948年信息论的创始人香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理。

我们先来看下面一个例子，对于一个正弦信号：

如果我们分别以0.5，0.25，0.1，0.01的间隔取点，然后再将每个点用直线连接起来。

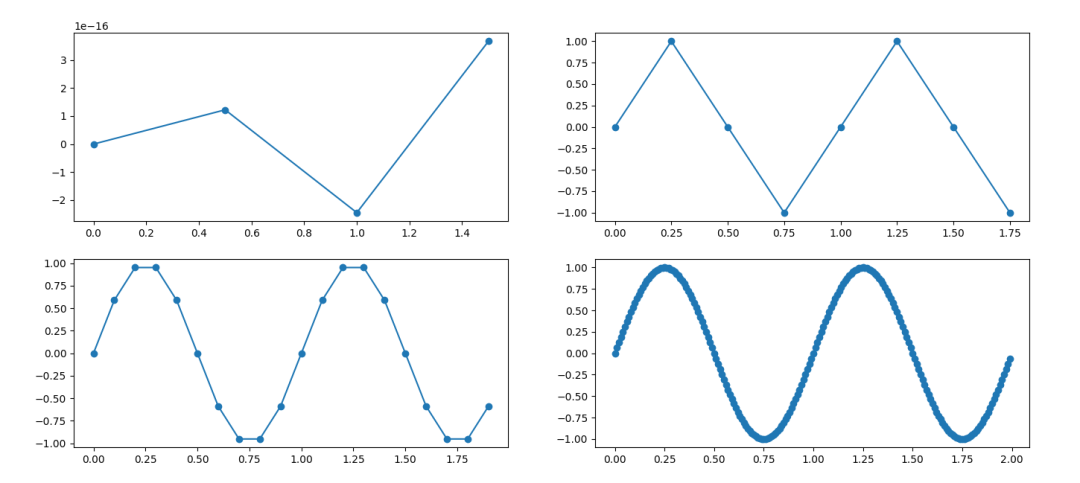
从上面的图中可以发现，时间间隔越小，记录这个信号的点数也多，信号还原的就越精确。显然，我们不可能无限多的点数去记录这个信号，如何才能准确的表达信号，又能合理的使用计算机资源？

其实大佬们早就有研究，就是我们今天要学习的奈奎斯特-香农采样定理。

采样频率要大于信号最高频率的2倍，才能无失真的保留信号的完整信息。

即：

这里，我们将这个信号频率（这个临界点）叫做奈奎斯特频率。下面我们不妨先通过一个实验来理解这个定理，假如有下面这样一个信号:

令f=5 Hz, 再分别依次以5Hz，10Hz，20Hz，40Hz，100Hz的采样率进行采样，观察不同采样率情况下时域和频域的信号还原情况，老规矩先上代码。

import numpy as np
import matplotlib.pyplot as plt

def signalCreate(_fs, _N, _f0):
    fs = _fs # 采样率
    N = _N # 数据点数
    f0 = _f0
    n = np.linspace(0, N-1, N)
    t = n / fs
    yt = np.exp(1j*2*np.pi*f0*t)
    f = n * fs / N - fs/2
    yf = np.fft.fftshift(np.fft.fft(yt))

    return t, yt, f, yf

t, yt, f, yf = signalCreate(5, 128, 5)
plt.subplot(5, 2, 1)
plt.plot(t, yt)
plt.subplot(5, 2, 2)
plt.plot(f, np.abs(yf))

t, yt, f, yf = signalCreate(10, 128, 5)
plt.subplot(5, 2, 3)
plt.plot(t, yt)
plt.subplot(5, 2, 4)
plt.plot(f, np.abs(yf))

t, yt, f, yf = signalCreate(20, 128, 5)
plt.subplot(5, 2, 5)
plt.plot(t, yt)
plt.subplot(5, 2, 6)
plt.plot(f, np.abs(yf))

t, yt, f, yf = signalCreate(40, 128, 5)
plt.subplot(5, 2, 7)
plt.plot(t, yt)
plt.subplot(5, 2, 8)
plt.plot(f, np.abs(yf))

t, yt, f, yf = signalCreate(100, 128, 5)
plt.subplot(5, 2, 9)
plt.plot(t, yt)
plt.subplot(5, 2, 10)
plt.plot(f, np.abs(yf))

plt.show()

结果如下图，左边是时域右边是频域。当采样频率是5Hz时，还原出来的信号是一个频率为0的直流信号，显然，这里当采样频率小于信号频率的两倍时是无法准确还原原信号的；当采样频率是10Hz时，还原出来的信号似乎也还是有些不对的地方，在频域上很明显信号不能完整的显示出来；当采样频率是20Hz时，不管是时域还是频域还原出来信号都已经很接近原始信号了；当然我们继续增加采样频率，当采样频率是40Hz和100Hz时，还原出的信号更加接近真实信号了。

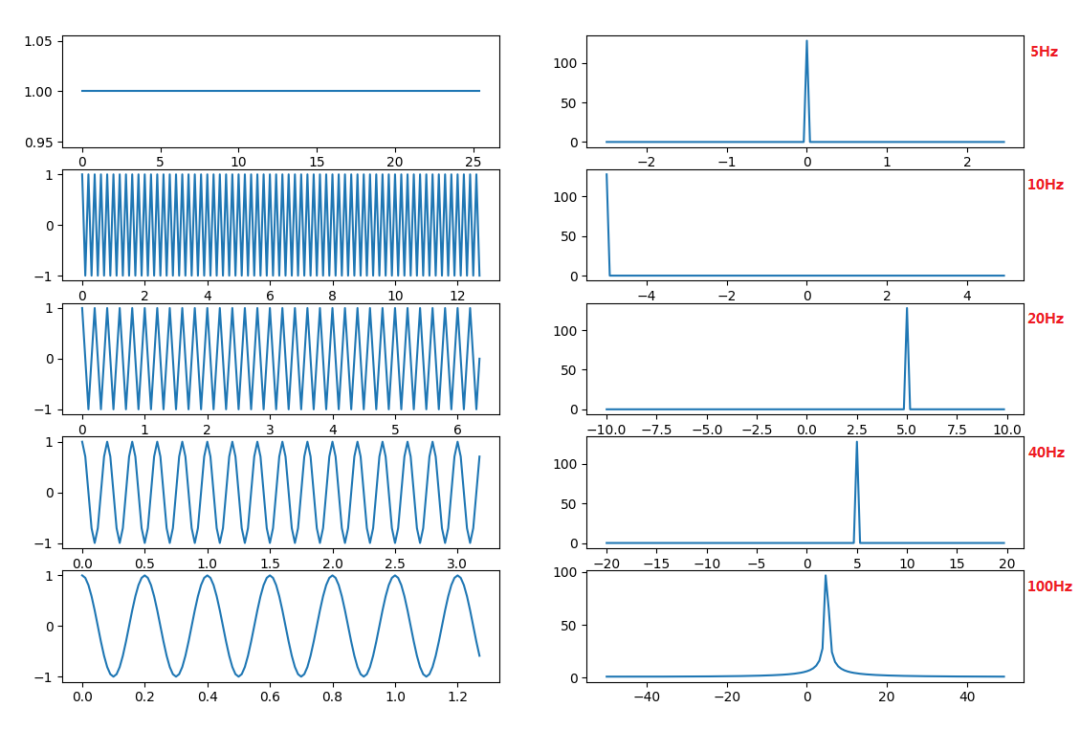不同采样率采样

不过，我们对比采样频率40Hz和100Hz的频域图形可以发现，100Hz的明显要“胖”一些。这是因为频率分辨率变大了，采样点数不变，采样分辨率随着采样频域增加而增加，采样分辨率可以用下面的公式计算：

显然，采样频率如果太低就不能正确还原真实信号；但是如果采样频率太高，会有较大的频率分辨率，同时又会有产生大量的数据。通常，在实际应用中采样频率会选择比两倍奈奎斯特频率要大一些（比如3～5倍）。

另外，在采样的过程中，对比采样频率和奈奎斯特频率大小关系，我们还可以这样来描述：

采样频率高于两倍奈奎斯特频率，这种采样被称为过采样；

采样频率低于两倍奈奎斯特频率，这种采样被称为欠采样。