

简单的聊聊什么是功率因数
工业控制
描述
在交流系统中, 电源提供正弦电压波形 , 负载则主导电流波形 。在加热器或白炽灯泡等最简单的“阻性”负载中,电流波形与电压波形形状一致,并且相位(时间轴)也保持一致。在下图中,电压与电流的乘积始终为正。 阻性负载的功率因数被定义为1 ,Φ=0,这意味着 100%的负载电流消耗成以W为单位的负载功率(有功功率,单位W)。
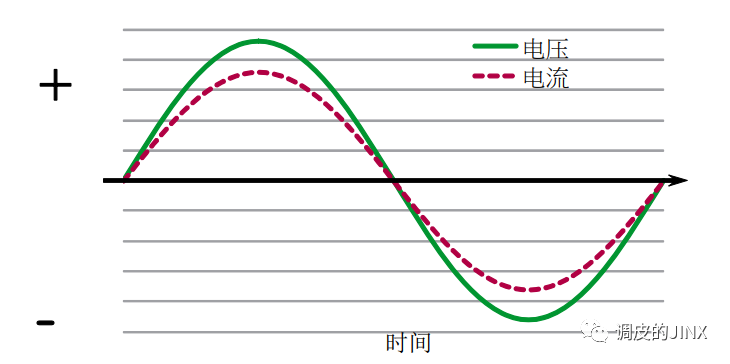
然而,很多类型负载虽消耗掉部分电流,却不用于以W为单位的功率消耗。通常来说,这些无法输送有功功率的电流,要么是因为电流在相位(时间轴)上与电压波形没有保持一致( 电流相位偏移 ),要么电流频率与电源电压不同( 谐波电流 )。下图显示了形状相同的两种波形(即没有谐波电流),但电流波形超前于电压波形90°。在这种情况下,电压与电流的瞬时值乘积在一半时间为正,另一半时间为负,也就是说输送至负载的功率在正负值之间交替变化,平均功率(W)为零。如果电流与电压相位偏移90°,周期内的平均功率就不会输送至负载。
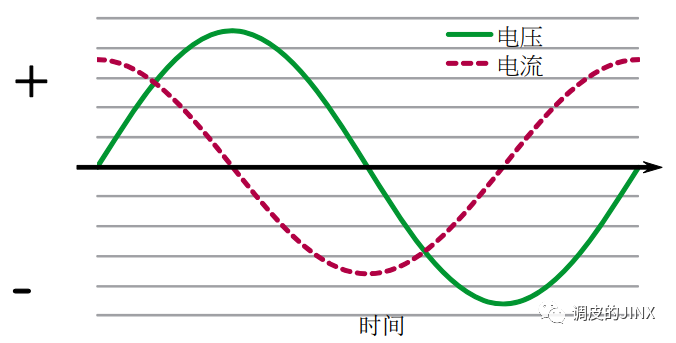
也就是说实际的负载电流可以分为三个部分: 与电压相位相同的电流部分 (输送有功功率的部分); 与电压相位偏移的电流部分 (不输送有功功率的部分);以及 载有谐波的电流部分 (也不输送有功功率)
功率因数可以是指用输送有功功率电流与总电流(包括相位偏移的电流和谐波电流)的比值 。因此,一个负载的功率因数始终介于0和1之间,其中1表示所有电流都用于给负载输送有功功率,而0则表示所有电流部分都没有用于给负载输送有功功率(即相位偏移或谐波电流)。

如前文所描述,我们知道 相位偏移和谐波电流均会使功率因数降低 ,那么这两种电流又是因何产生?
相位偏移的电流在通常被称为“无功电流” , 无功电流是由“感性”或“容性”负载引起的 。
对于电动机等感性负载而言,电流滞后于电压而引起相位偏移(电感特性:电感比较倔强,反应慢半拍**。),因此感性负载被认为具有“滞后”功率因数。**
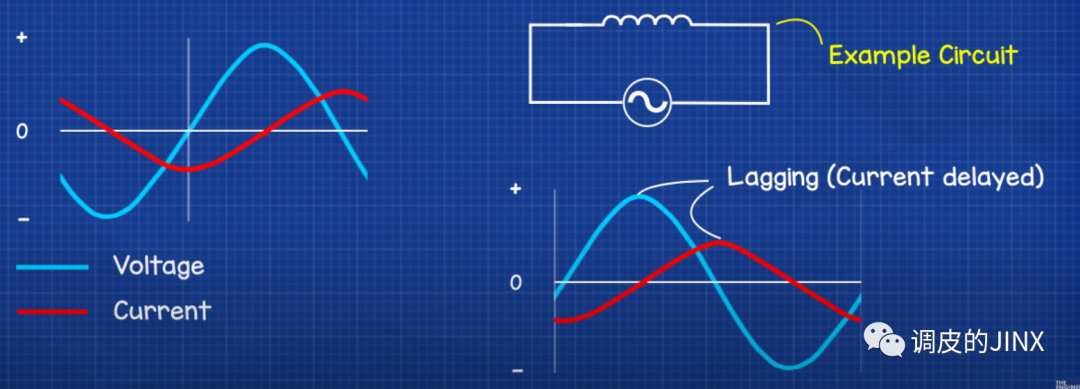
对于容性负载而言, 电流超前于电压电流滞后于电压而引起相位偏移(电容特性:电容比较敏感,反应快半拍**。**),因此 容性负载被认为具有“超前”功率因数 。
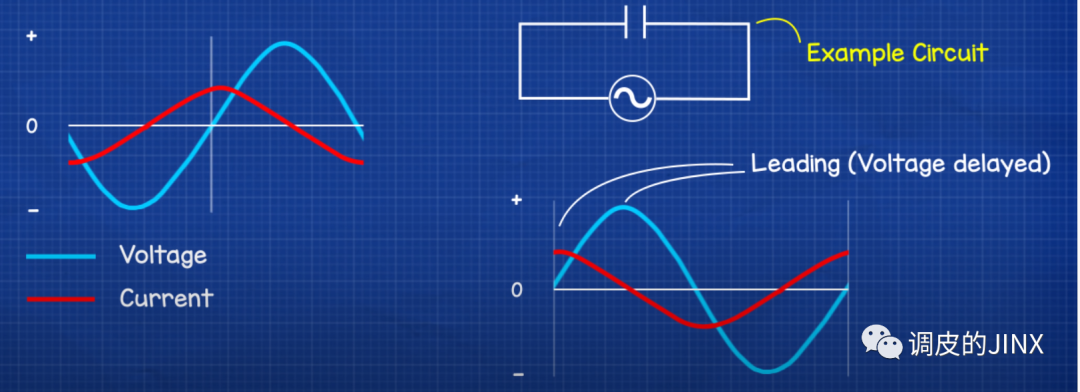
谐波电流是由所谓的“非线性”负载引起的,这些负载的电流波形在形状上不同于供电电源的电压波形 。
这里需要稍微解释下几个名词。
所谓非线性,就是自变量和变量之间不成线性关系,成曲线或者其他关系。用函数解释则为:y=f(x),当为一次函数时,y与x是线性关系,为其他条件则为非线性关系。
万能的傅里叶变换告诉我们:任何周期性波形均可分解为一个基频正弦波加上许多谐波频率的正弦波。
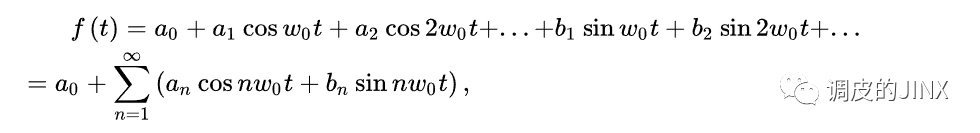
一般周期性波形不是完美的正弦函数或余弦函数,也就是说波形存在畸变 ,因此根据上述傅立叶变换,周期函数都可以展开为常数与一组具有共同周期的正弦函数和余弦函数之和。
其展开式中, 常数表达的部分称为直流分量 , 最小正周期等于原函数的周期的部分称为基波或一次谐波 ,最小正周期的若干倍等于原函数的周期的部分称为高次谐波。因此高次谐波的频率必然也等于基波的频率的若干倍,基波频率3倍的波称为三次谐波,基波频率5倍的波称为五次谐波,以此类推。 不管几次谐波,他们都是正弦波 。
开关电源控制的电机就是典型的非线性负载,这也就是为什么驱动电机技术经常会听到“谐波”的原因。各种驱动电机技术的提升和改进也在围绕谐波进行。
-
功率因数计算公式_功率因数与什么有关_提高功率因数的方法2017-08-07 29965
-
如何区别主动式功率因数校正?2022-10-08 0
-
功率因数提高2008-12-11 901
-
功率因数补偿原理2008-08-18 9117
-
功率因数的测量2016-05-27 1942
-
功率因数分析大全(功率因数的计算公式,功率因数对照表,功率因数和无功率比值分析)2017-07-06 88325
-
什么是功率因数_功率因数计算公式_提高功率因数的方法2017-08-07 31735
-
功率因数角2017-08-27 36545
-
功率因数的简单测量威廉希尔官方网站2017-10-09 3365
-
为什么功率因数会出现负值2019-06-04 60873
-
什么是功率因数?功率因数的详细解析2019-06-16 166363
-
什么是功率因数补偿 功率因数的校正2022-09-30 1075
-
什么是功率因数 功率因数校正基础知识2023-10-05 2736
-
威廉希尔官方网站 的功率因数怎么计算 功率因数偏低如何解决2024-02-14 5386
-
什么是功率因数? UPS负载功率因数介绍2024-04-05 2206
全部0条评论

快来发表一下你的评论吧 !

