

无需附加传感器的升压PFC变换器输入功率估算可行性与准确性分析
电子说
描述
无需附加传感器的升压 PFC 变换器输入功率估算可行性与准确性分析
概述
PFC 变换器广泛应用于工业领域,它通过主线路提供直流输出电压,并同时保持高功率因数 (PF) 和低电流失真。其中部分应用,如电信、服务器、工作站电源和插电式电动汽车等,都需要实时测量有功输入功率以监控能耗,并实现系统效率的提升与智能系统管理。通常情况下,在桥式整流器前面添加专用的电压和电流传感器可以实现这种功率计量功能。但是,无论附加的传感器是基于分流还是基于霍尔效应,都会使电源成本、复杂性和功耗大幅增加。
根据升压 PFC 变换器的基本建模[1],PFC 控制器通常会对输入电压、输出电压和电感电流进行采样,以控制开关频率和占空比。这样,在输出功率得到调节的同时整形输入电流,从而实现高 PF 和低总谐波失真 (THD)。因此,PFC 控制器通常拥有可用于功率估算的原始信息。鉴于数字控制器已为业界广泛采用[2、3、4],通过 PFC 控制器的数字通信接口通常可以实时访问这些信息。这样,我们就可以创建一种通过间接计算来监测输入功率的方法,取代通过额外电压和电流传感器实现的传统功率计量方法。
为了估算实际输入功率并达到可接受的准确度,有几个必须考量的关键因素。首先要考虑输入端的无源元件,例如,电磁兼容 (EMC) 元件和桥式整流器会造成升压变换器调节功率与实际输入电流之间的差异。不过,这不是主要问题,因为无源元件引入的额外功率很容易建模[5]。换句话说,该功率可根据设计的威廉希尔官方网站 参数直接计算出来,尤其是考虑到高频失真并不是基本功率计量要求的主要关注点。然而,一些非理想效应却会对电感电流估算的准确性产生较复杂的影响。例如,导通和关断延迟会使实际电感电流和开关频率偏离控制目标。DCM 中的寄生振荡也会为电感电流引入了另一个变量。此外,这些影响还都随工作条件而变化。大多数实际应用都采用多模式控制方案[6、6、7、8、9],因为其轻载性能优于传统的临界模式 (CrM) 控制方案或固定频率连续导通模式 (CCM) 控制方案。为了准确估算功率,设计人员必须考虑各种操作条件下的这些非理想效应。由于 PFC 模型 [10] [10]具有可观测性,即使不采样电感电流[11、11、11、12],PFC 控制方案也能实现。因此,由延迟引入的电流误差也可基于其他系统状态和参数的适当建模而得到补偿,例如输入和输出电压,以及 PFC 电感。另一方面,DCM 中的寄生振荡也可在时域中建模[13、14],这样,每次开关产生的相应误差都可以被推导出。
本文基于多模式 PFC 控制方案详细分析了这些效应产生的影响,并提出了一种经过改良且易于实现的输入功率估算法,以实现宽工作范围内精确的有功功率估算 。我们采用数字 PFC 和 LLC 组合控制器 HR1211GY构建一个额定功率为 400W 的原型。该控制器采用多模式 PFC 控制方案,可实现 CCM 和 DCM 操作模式之间的平滑转换。通过这种业界主流控制方案的实验结果,可以验证该估算方法的可行性和普遍适用性。
多模式PFC控制方案
如图 1 所示,采用典型多模式 PFC 控制方案的升压变换器可实现 CCM 和 DCM模式之间的平滑转换,从而实现宽工作范围内的高效率。CCM模式可以最大限度地降低重载条件下的峰值电流和 RMS 电流,这有助于减小磁性元件的尺寸,使其适用于要求良好效率的大功率应用。具有较低开关频率的 DCM 模式则可以最大限度地降低开关损耗,从而实现轻载条件下的高功率。而在中等负载条件下的CCM 和 DCM 混合模式则可以更好地在传导损耗和开关损耗之间取得平衡,实现更佳的平均效率。这种新兴的混合模式控制方案近来在业界得到认可,因为满载效率和轻载效率对大多数实际应用来说都同样重要。
如图 1 所示,这种控制方案对输出电压 VO 进行采样,并将其与输出参考电压 VOREF( OREF) 进行比较,以通过 PI 环路调节器得出内部补偿状态 v竞争和竞争(n) 。相应地,内部电流环路也为电感电流控制生成参考,公式如下:
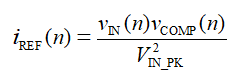
其中, vIN(n) 是采样的瞬时输入电压,而 VIN-PK 印尼语 是线路周期中的峰值电压。
该方案在每个开关周期内 ,在MOSFET 关断之前采样电感峰值电流iPK(n),并将 2iREF(n) 与iPK(n)进行比较,由此确定变换器应该工作于 CCM模式还是 DCM 模式。如果工作于 CCM 模式,则开关频率 fS 被调节为最大开关频率fS_MAX ,并作为稳态频率。为保持每个开关周期的平均电流等于 iREF(n),每当电感电流 iL 下降到目标谷值i有效时,MOSFET即导通。公式如下:
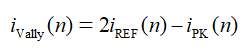
与此同时,为保证 PFC 电感的励磁平衡,控制导通时间 TON(n) 为:
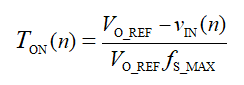
如果工作于 DCM模式,仍以相同方式控制导通时间,但降低开关频率以保持平均电流等于 iREF(n)。通常,开关频率被控制为:
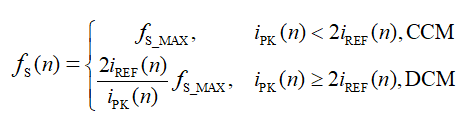
这样,在一个开关周期内的平均 iL 始终等于 iREF。理想情况下, iREF 可用于计算输入功率。但是,如果不对非理想效应进行补偿,仍将无法保证估算的准确度,以下章节将对此进行详述。
寄生效应引起的电流控制误差
在升压变换器中,导致实际电流与控制目标之间误差的主要寄生效应来自开关延迟和电流振荡。这些效应与变换器的参数有关,并随工作条件而变化。
在 CCM 模式中,误差主要由导通延迟 T吨 吨 吨 和关断延迟 TD_ offFF引入,如图 2 所示。导通延迟将导致低于目标电流谷值的下冲,而关断延迟则使采样点偏离电感电流的实际峰值点。一个开关周期内的平均误差计算公式如下:
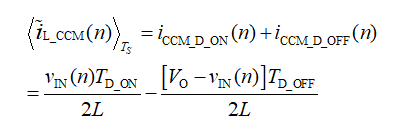
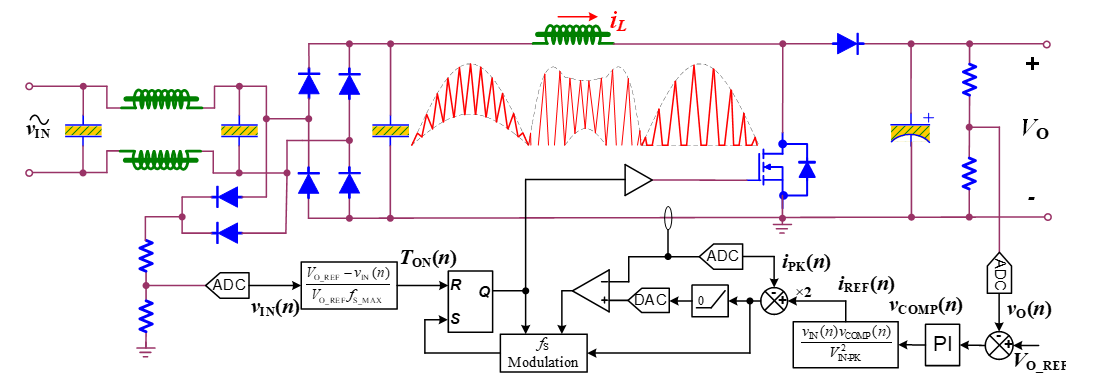
图 1:采用多模式 PFC 控制方案的升压变换器
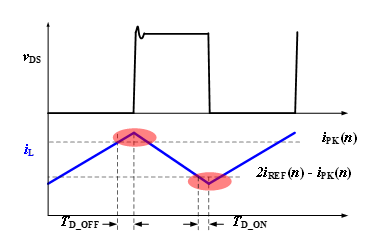
图 2:CCM 模式中导致电流误差的主要原因
其中, L 为 PFC 电感感量。
在 DCM 模式中,电感电流总是从零开始,因此导通延迟不会影响电感电流,如图 3 所示。然而,关断延迟对电感电流的峰值采样仍有类似的影响。但其误差模型与 CCM 不同,因为它对电流峰值和占空比均有影响。在一个开关周期内,由 DCM 关断延迟引起的的平均误差可以表示为:
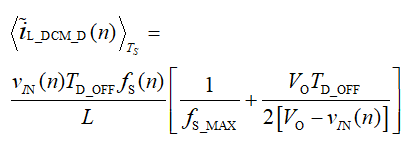
另外,DCM 振荡也是电流误差的另一个主要原因。当 PFC 电感电流降至零时,电感随 MOSFET 和续流二极管的等效寄生电容而振荡。振荡的初始状态伴随零电感电流和VO 处的漏源电压 vDS 。由于 MOSFET 体二极管的钳位效应,振荡有两种可能的情况,具体取决于 vDS 是否振荡为零。
如图 3(a)所示,当 vIN 超过 VO / 2 时,振荡以自由阻尼方式进行,不会被钳位至任何一点。一个开关周期内的平均振荡电流可表示为:
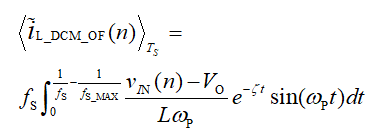
其中, ωP 和 ζ 是角频率和振荡的阻尼系数。
如图 3(b)所示,当 vIN 低于 VO / 2时,当 vDS 降至零时,振荡被体二极管钳位。钳位期间,电感电流以恒定斜率上升,直到电流极性再次反转。然后,恢复自由振荡。本场景中的振荡由三个部分组成,前两个部分的持续时间可分别计算如下:
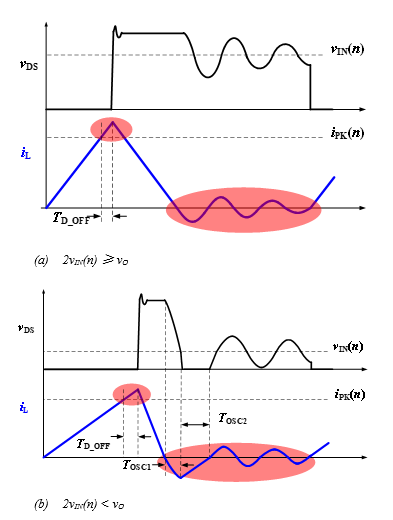
图 3:DCM 模式中导致电流误差的主要原因
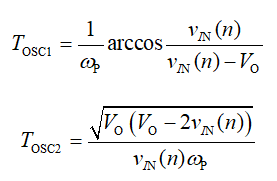
由此可以得到一个开关周期内的平均振荡电流,公式如下:
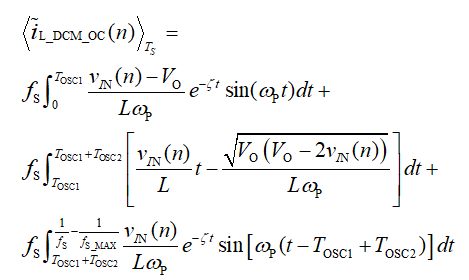
基于此,DCM 中的一般电流误差为:
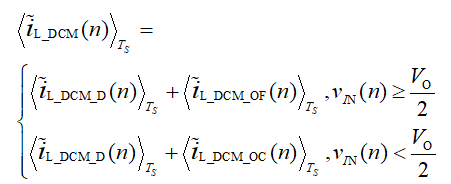
在每种操作模式下,由寄生效应引起的电流误差通过 公式 (5) 至公式 (11) 计算。但是,如果要在实际应用中采用一个通用的电流误差补偿算法,还需要考虑各种条件之间的边界情况。假设在 AC 输入线周期的第一个1/4周期内,CCM 和 DCM 之间的转换角为 θT,则边界导通处的输入电压和参考电流为:
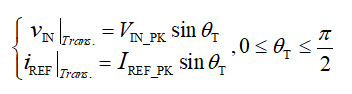
其中 IREF_PK 是一个完整线路周期中的峰值参考电流,可根据公式 (1) 通过v竞争和竞争 推导。交流输入线每1/4周期中的转换角都彼此对称。
由于电感电流在转换点也处于边界传导状态,因此有下式:
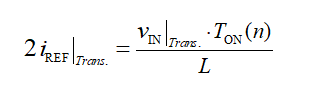
根据公式 (2)、(12)、(13),可以推导出

相应的 θT 分布如图 4 所示。当 θT 为 0 时,变换器仅在 CCM 模式下工作。当 θT 等于 π / 2时,变换器仅在 DCM模式下工作;当 θT在 0 和 π / 2之间时,变换器在一个 AC 输入线周期内同时工作于CCM 和 DCM 模式,而且随着负载增加或输入电压降低,工作于CCM 模式的时间会增加。
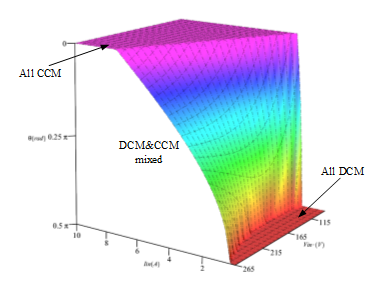
图 4:CCM 和 DCM 工作模式分布 vs. 输入和负载条件
有功输入功率估算
有功输入电流可以通过补偿各种工作条件下的寄生效应来精确估算,如第3部分中的分析所示。为了获得有功输入功率,还需要考虑输入端无源元件引入的功率损耗。
以图1所示的原理图为例,PFC变换器输入端的无源元件主要包括LC滤波器和桥式二极管。流过滤波器电容的无功电流对有功功率没有贡献,而且电容的漏电流足够小,因此,滤波器电容对有功功率的估算影响不大。但桥式二极管引入的压降和滤波器电感的寄生电阻则会带来相当大的功率损耗,必须将其纳入功率估算之中。无源元件之前的输入电压可通过下面的公式推导:
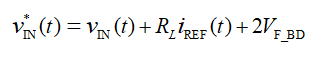
其中, V发 发 发 发 发 是桥式整流二极管的正向电压, RL 是所有滤波器电感的总等效电阻, vIN(t) = VIN-PK 印尼语sinωLt 是 PFC 控制方案中基于采样输入电压 vIN(n) 的重构电压, ωL 则为输入线频率。
综合以上所有的分析,有功输入功率可通过以下公式估算:
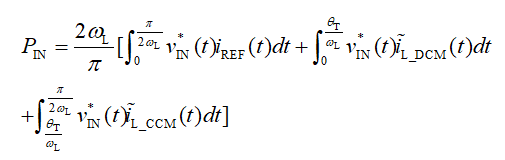
实验验证
为了验证对输入功率的分析和提出的估算方法是否准确,我们构建并测试一个 400W 的原型。该原型采用数字多模式 PFC 和 LLC 组合控制器HR1211GY设计并实现。其PFC 级的威廉希尔官方网站 和控制方案与图 1 相同,原型照片如图 5 所示。PFC 级的规格和关键元件参数包括 V内 文 号= 90V - 265V,fL= 50赫兹,RL=100立方米,V发 发 发 发 发= 0.75V,VO= 400V, = 400V,fS_MAX= 100kHz,L = 190µH, 原边 MOSFET IPP60R099C7XKSA1、续流二极管STPSC406D 、 ωP= 5.93×106弧度/秒,T吨 吨 吨 = 300ns 和 TD_ offFF = 150ns。而功率估算所需的其他瞬时状态,如 v竞争和竞争, VIN-PK 印尼语 和 VO,都可以通过 HR1211GY 的集成 UART 接口实时访问。
输入电流和 PFC 电感电流的波形如图6所示。图中显示了 PFC变换器在低压和满载条件下完全运行于 CCM 模式。开关频率固定为 fS_MAX,电流峰值和电流谷值均调节为正弦波。
图 5:采用 HR1211GY 构建的 400W 实验原型
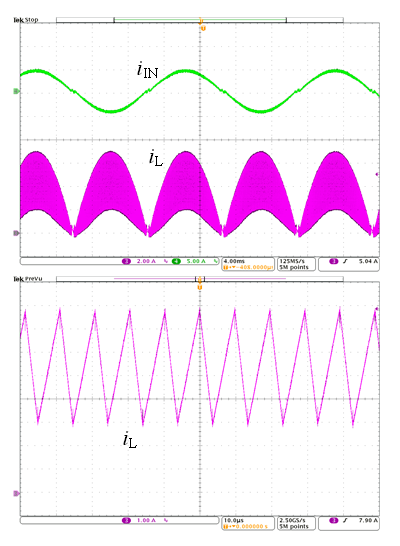
图 6:实验波形(VIN_rms = 110V 、PO = 400W)
在高压线和满载条件下,PFC 变换器工作于CCM 和 DCM 混合模式,如图 7 所示。波形显示出电感电流在 CCM 和 DCM 之间的转换。峰值电感电流在输入线的峰值处较低,但电感电流的开关周期平均值仍由控制器调节为正弦波。
在轻载条件下,PFC 变换器完全工作在 DCM模式,如图 8 所示。开关频率随负载的下降而降低。
采用本文提出的功率估算方法,根据上述原型的参数和从数字控制器 HR1211GY 中读取的瞬时状态,可以计算出从 10%到100% 负载条件下的输入功率。图 9 对计算结果和使用WT310E功率计得到的实际测量结果进行了对比。
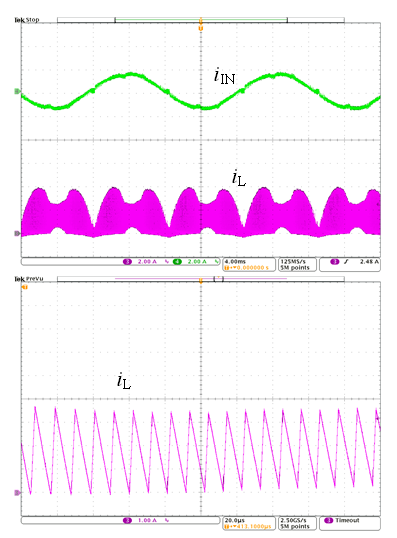
图 7:实验波形(VIN_rms = 230V 、 PO = 400W)
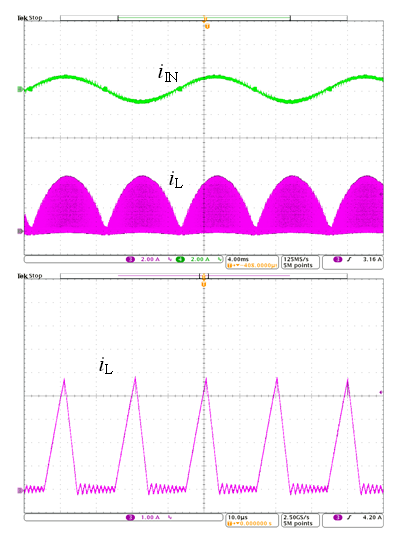
图 8:实验波形( VIN_rms = 110V 、PO = 100W)
可以看出,在宽负载范围内的估算误差小于 3%。而且,相同的估算法可覆盖各种不同的输入条件。
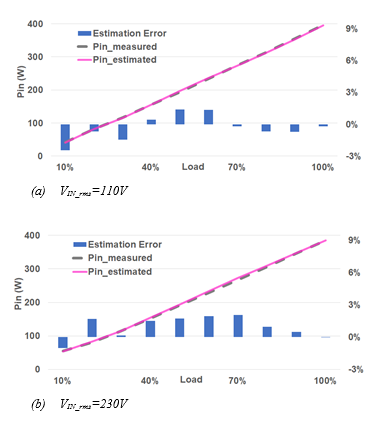
图 9:计算输入功率与测量输入功率的对比
结语
本文探讨了在没有任何附加传感器的情况下,对升压 PFC 变换器的有功输入功率进行估算的可行性。分析考虑了各种寄生效应的影响,例如导通和关断延迟、DCM 振荡、DCM 和 CCM 之间的转换以及无源元件的有功功耗。根据系统和寄生效应的数学建模,我们提出了一种准确估计输入功率的算法。它考虑了主流多模式PFC控制方案的特点,能够支持宽工作范围。通过基于 HR1211GY构建的 400W 升压 PFC 原型的实验结果,该估算法已得到验证。数字 PFC 控制器在实际应用中越来越常见,本文提出的功率估算法可降低系统复杂性与成本,同时在不添加任何额外传感器的情况下实现基本功率计量功能,助力提升未来电源产品的可靠性。
审核编辑:汤梓红
-
路面检测方案比较及可行性分析2011-07-12 0
-
气体传感器研发的可行性报告2015-05-05 0
-
关于PFC实验装置负载测量准确性的问题2018-05-11 0
-
flightsense传感器的准确性怎么样?2018-09-12 0
-
3KV有源PFC升压变换器2008-05-03 905
-
升压变换器,升压变换器输入输出电压关系及Boost威廉希尔官方网站 拓补结2009-05-12 10429
-
单级功率因数校正(PFC)变换器的设计2009-07-07 1368
-
升压变换器基本威廉希尔官方网站2009-07-20 1518
-
PFC变换器输入电流过零畸变校正2011-02-23 1708
-
典型的PFC升压变换器威廉希尔官方网站2011-10-17 5281
-
管壳式换热器温度传感器测量的准确性校正_王金辉2017-01-17 606
-
低温余热制冷系统温度传感器测量准确性研究_栗鹏飞2017-01-19 659
-
从adis16210传感器来分析信号准确性的重要性2017-09-14 895
-
基于传感器准确性的医疗应用2019-04-02 2198
-
非线性损耗模型:提升SiC变换器性能估算的准确性2024-12-04 731
全部0条评论

快来发表一下你的评论吧 !

