怎样从传输线的等效威廉希尔官方网站 推导出传输线的电报方程呢？

（一）

传输线可以等效为电阻，电感串联，电导，电容并联，如下图所示。

 

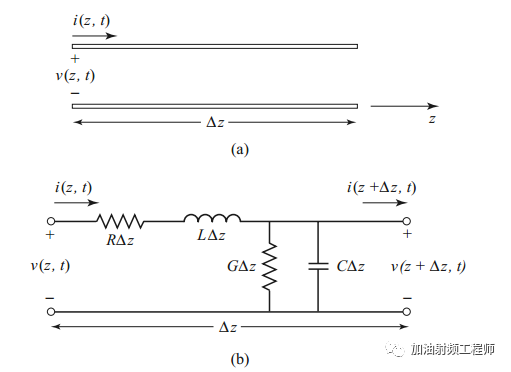
这个等效图，可以这样理解。

首先，这个图取的是传输线上无线小的一段，dZ，而传输线是由无数段这样的小段组成的。

以微带线为例，上层和下层导体，为做了表面处理的铜，而铜具有有限的电导率，所以为有电阻效应。

同时，微带线上层和下层导体之间形成的电流环路，会产生电感效应。

然后，上层和下层导体之间的介质，有介电损耗，等效为电导。

电容就很容易理解了，上层和下层导体，再加上中间的介质，妥妥的电容效应。

然后就利用基尔霍夫电压定律和基尔霍夫电流定律，就能得出下面的等式。基尔霍夫电压定律就是说闭合环路上的电压和为0；基尔霍夫电流定律就是说流入一个节点电流等于流出该节点的电流。

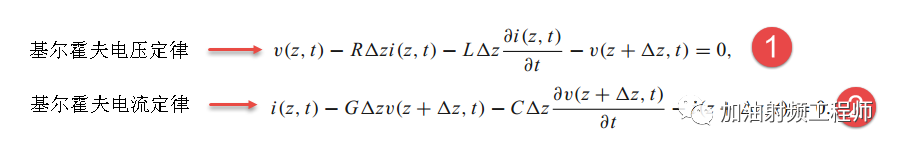
将式1和式2除以△z，并使得△z—>0，可以得到下式：

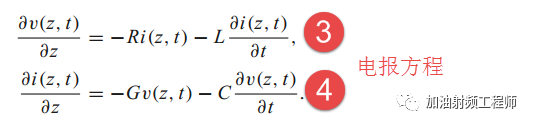
如果电压和电流都是时谐场的话，即都是电磁场随时间余弦或正弦变化，则电压和电流都可以用相量来表示。

即v(z,t)=Re{v(z)exp(jwt)}，i(z,t)=Re{i(z)exp(jwt)}

相量表示时，式中没有exp(jwt)和Re{.}，这是因为大家达成共识，不用写，但是实际上是有的。

所以用相量表示后，上述中的式3和式4，即可得到：

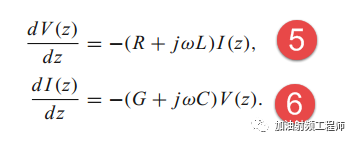
然后把6式代入5式，即可得到式7；同样，把式5代入式6，即可得到式8。

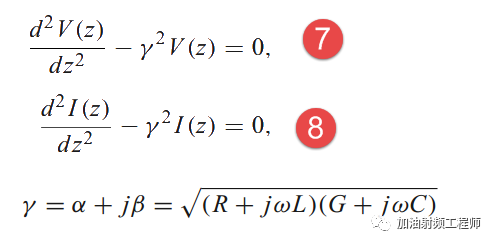
式7和式8的解为：

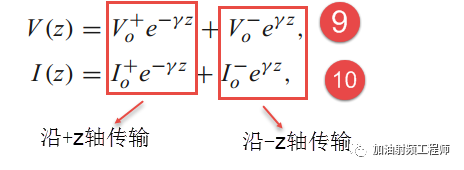
如果把式9代入式5，可以得到：

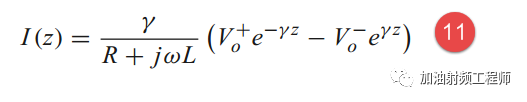
与式10一对比，即可得到：

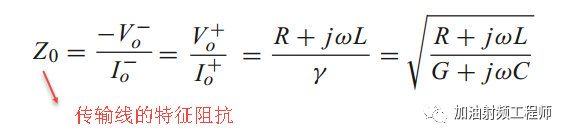
在很多实际应用中，传输线的损耗很小，可以被忽略，从而使得计算过程得到简化。

忽略传输线的损耗，即使R=G=0，

所以可以得到：

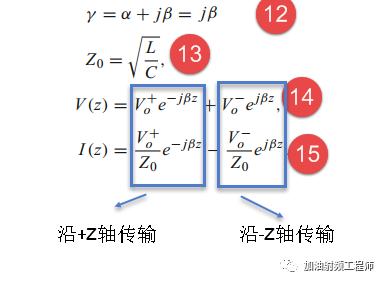
（二）

从上面得到的传输线上的电压和电流的表达式中，可以看到，电压和电流的表达式，都分为两个部分，一个沿+z轴传输的波，另一个沿-z轴传输的波，即一个入射波，一个反射波。

假设一个传输线，终端的负载阻抗为ZL，ZL为任意值，且假设负载的接入处为z=0处。

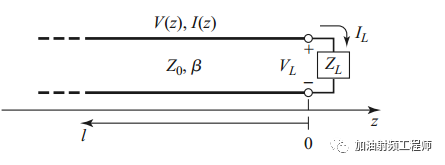
假设，从z<0处，有一个来自源端的入射波，形式为：

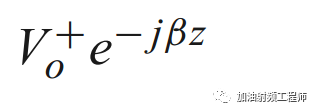
然后到达负载处，为产生一个反射波，此时传输线上的总电压，如式14和15所示。

z=0处，电压和电流的比值，即等于负载阻抗的值，即：

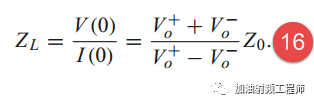
所以，传输线上的电压反射系数为：

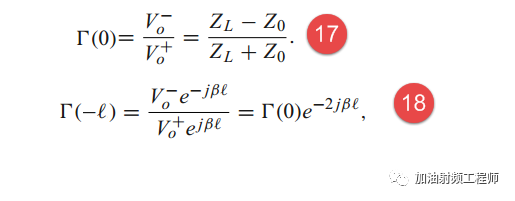
传输线上的输入阻抗为：

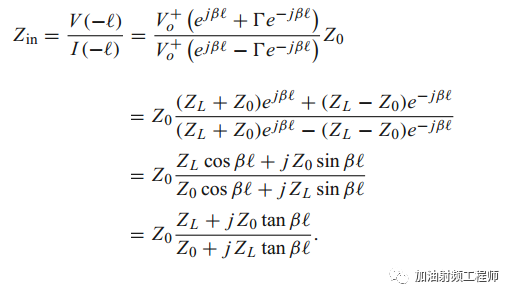
审核编辑：刘清