基于四分之一波长传输线的阻抗匹配原理

在微波频段，特定特征阻抗的四分之一传输线是个宝贝，经常被用来做匹配。

比如说，负载阻抗是100ohm，我现在想把这个100ohm匹配到50ohm怎么办？

用一个特征阻抗为70.71ohm的，长度为四分之一波长的传输线，就可以。

为什么呢？

首先，从传输线上的阻抗看起。

如下图所示，传输线的线长是四分之一波长，特征阻抗为Z1，负载电阻为RL。

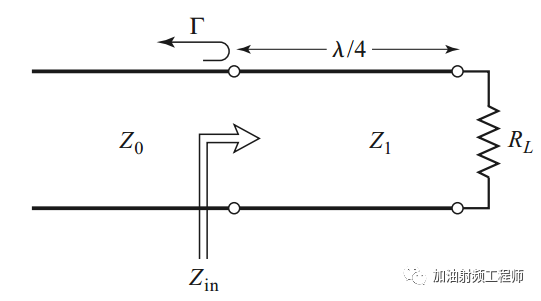
由传输线上的电压和电流的表达式，可以推导出，传输线左侧看进去的阻抗为：

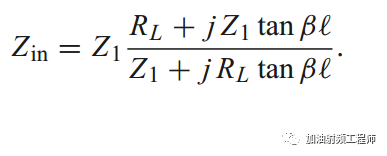
因为传输线的长度为λ/4，所以 β = (2π/λ)(λ/4) = π/2，从而可以得到：

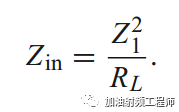
为了使从 λ/4传输线看过去的反射系数为0，则需要Zin=Z0。

所以，

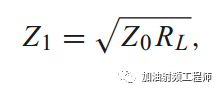
也就是说，当长度为λ/4的传输线的特征阻抗是源电阻和负载电阻的几何平均数时，虽然在λ/4匹配传输线上有驻波，但是馈线上没有反射。

很神奇，是吧？

从公式推导来看，是上面的这样的结果。但是为什么会产生这样的结果呢？

玄机就在下面的这幅图中。

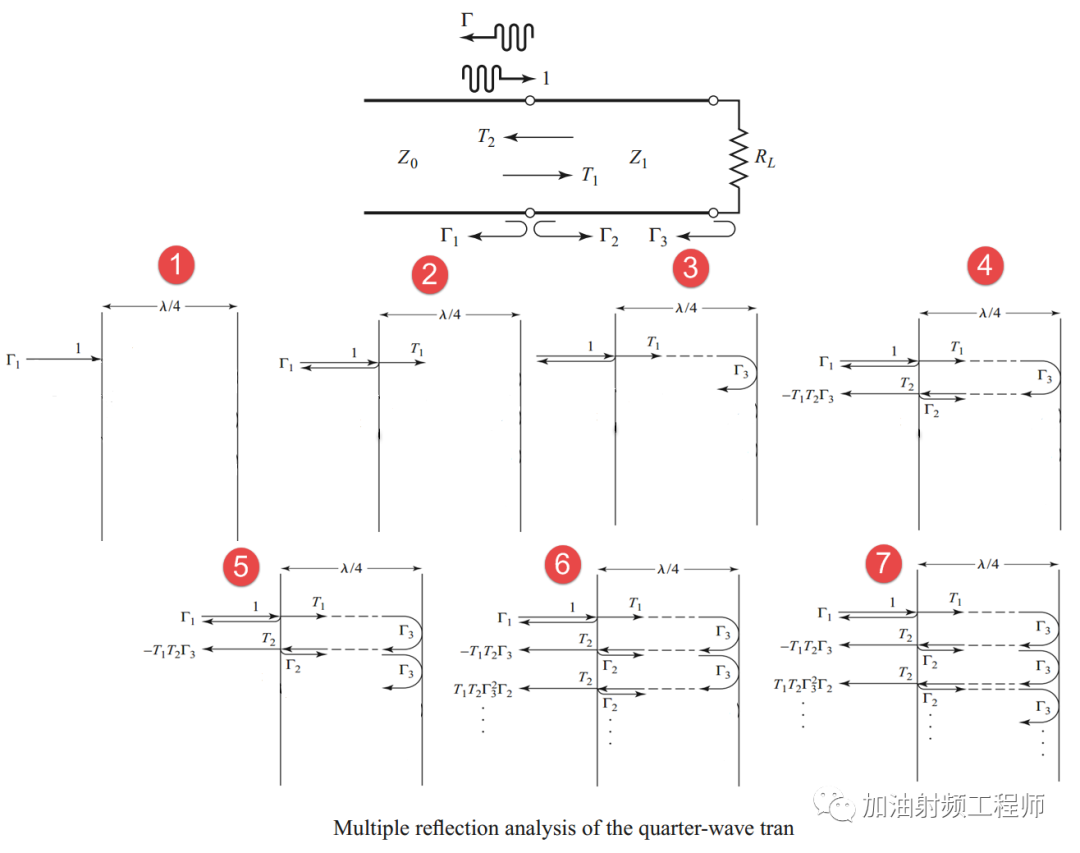
当一个入射波，进入传输线时，它会经历多重入射和反射。

而馈线上的反射系数为：

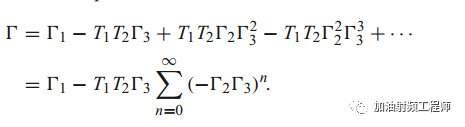
其中的负号，是因为每经过两次四分之一波长的传输线，会产生180度的相移。

因为：

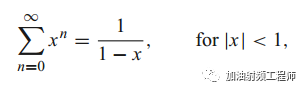
所以：

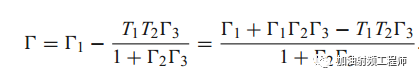
而：

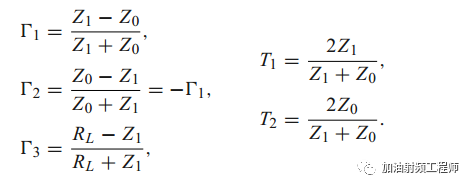
因此：

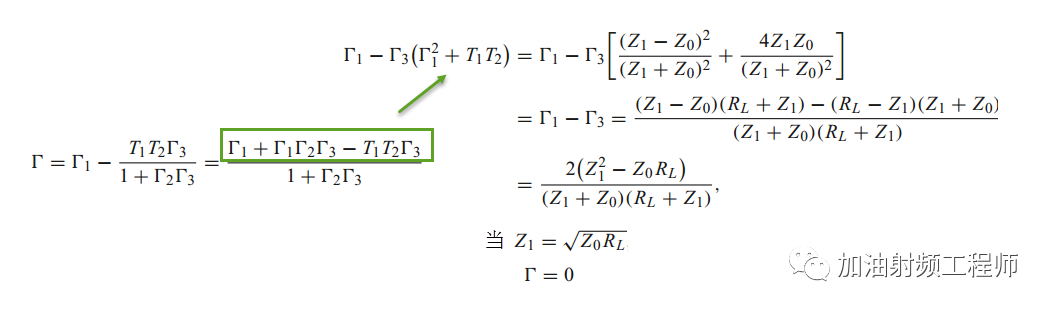
也就是说，当传输线的长度为四分之一波长，且特征阻抗满足一定条件的情况下，虽然瞬态的反射系数不为0，但是在经过无数次反射后，稳态情况下馈线上的反射系数为0。

所以，利用四分之一波长的传输线(体现在180度相移上)，可以将一个实阻抗匹配到50ohm，或者其他实阻抗。

　　审核编辑：汤梓红