为什么要引进傅里叶级数？傅里叶级数的物理意义是什么？

谈到傅里叶级数，我们先要谈傅里叶变换。笼统来说， 傅里叶变换的目的将一个信号从时域变换到频域进行分析，原因是很多在时域内看不见的特性在频域内能很清楚地得到。 比如说，矩形波，在时域内就一条直线，当用傅里叶变换后在频域内，我们就能看见各谐波的频率，相位，振幅等等信息，会给我们分析问题带来很大的方便。同时，傅里叶变换把函数变换为正弦或余弦，正余弦函数的好处就是其微分和积分也是正余弦，计算起来很方便。同时，根据欧拉公式，正余弦函数是指数为复数的指数函数，指数函数的微分积分也是它本身，这也给我们提供了非常方便的计算途径。

而要得到傅里叶变换，首先要研究周期信号的傅里叶变换（周期信号相对比较有规律），也就是傅里叶级数。简而言之，傅里叶级数是为了研究周期信号在频域上的特性而孕育而出的一个概念。

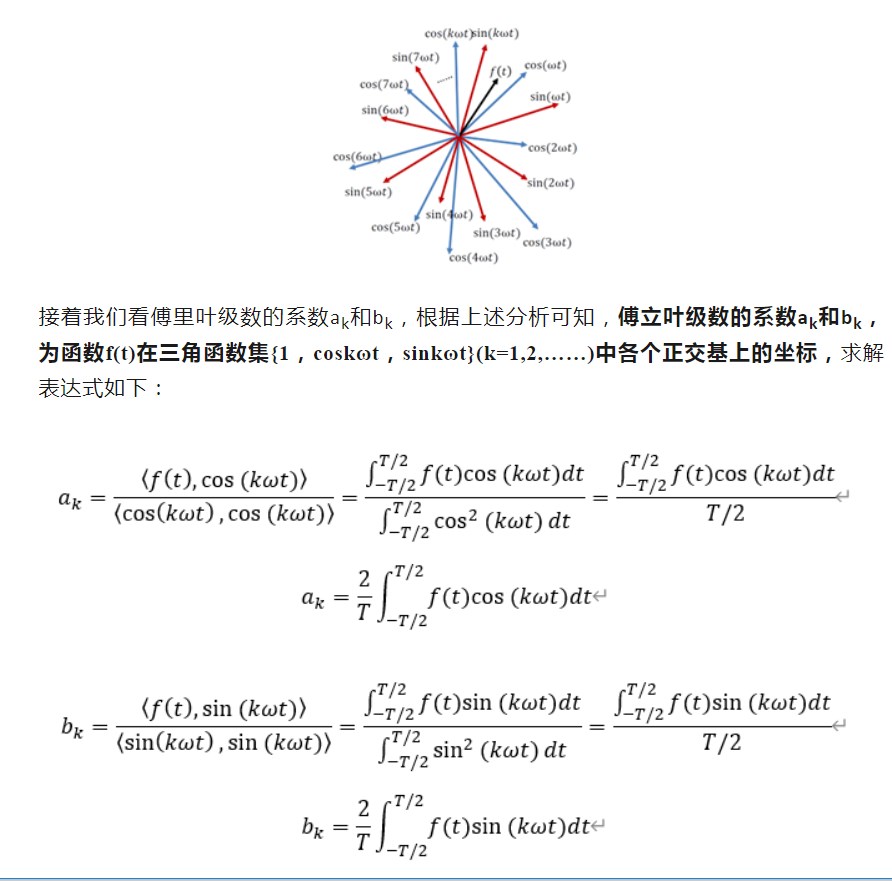
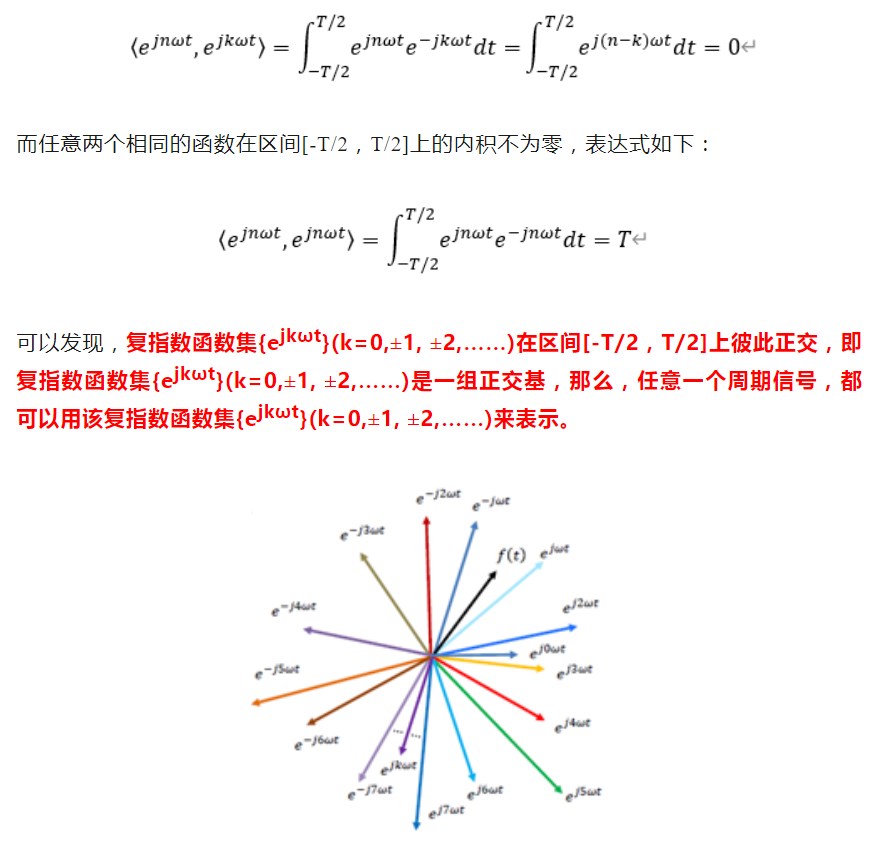
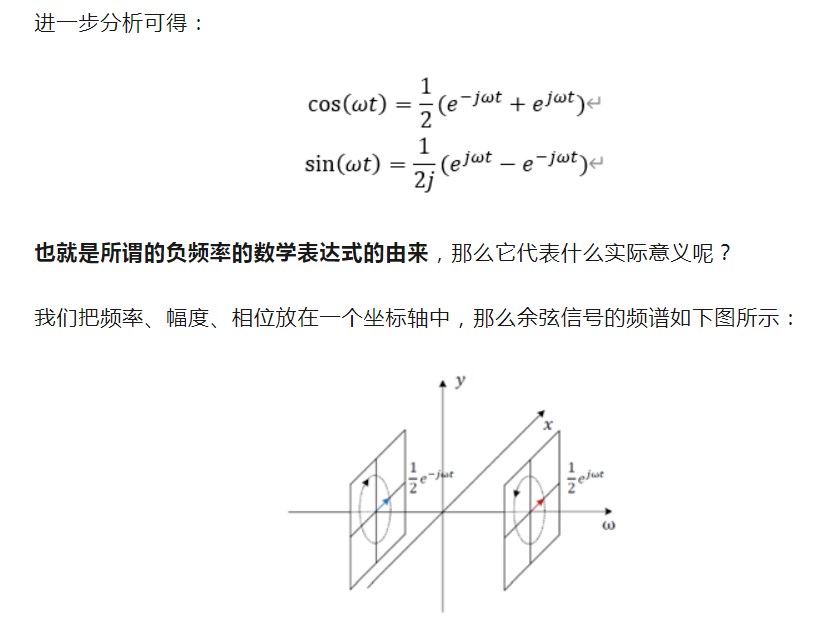
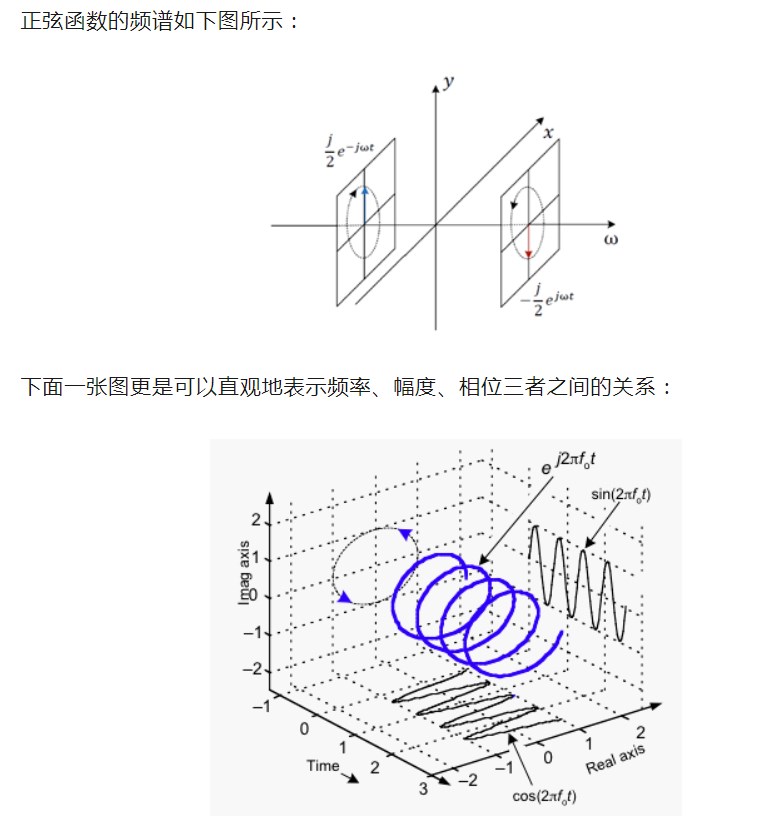
那么第二个问题的答案就呼之欲出，傅里叶级数的物理意义是什么？其实200多年前，傅里叶老爷爷就揭示了，他在书中说到：“ 任何一个周期信号都可以用正弦函数级数（也就是和）来表示。 ”换句话说，傅里叶级数的物理意义，就是把周期信号，用无限的周期正余弦函数进行叠加，来表示我们所需要的时域的函数。

下面具体进行分析。

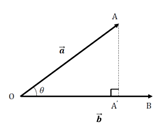
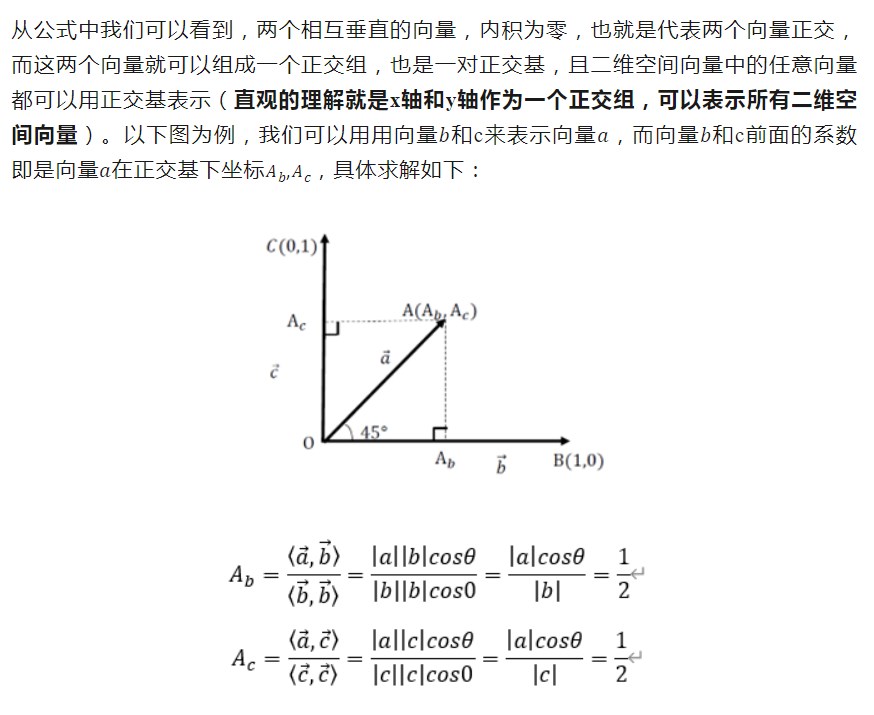
我们先来复习一下实向量（以下简称向量）的内积（也叫作点积），两个向量的内积等于其中一个向量的模与另一个向量在这个向量方向上投影的乘积，用公式表达即为：