

用Python进行线性回归 用Python中的mlxtend包实现关联规则挖掘
电子说
描述
1.简单线性回归
读取Case1.csv,其中wt列为病人体重,volume列为病人肾脏容积,试建立回归方程,用病人体重预测病人肾脏容积。
2.多元线性回归
读取Case2.csv,其中CRIM列为城镇人均犯罪率,ZN为住宅用地超过25,000平方英尺以上的比例,INDUS为城镇非零售商用土地的比例(即工业或农业等用地比例),CHAS为查尔斯河虚拟变量(边界是河,则为1;否则为0),NOX为一氧化氮浓度(百万分之几),RM为每个住宅的平均房间数,AGE为1940 年之前建成的自用房屋比例,DIS为到波士顿五个中心区域的加权距离(与繁华闹市的距离,区分郊区与市区),RAD为高速公路通行能力指数(辐射性公路的靠近指数),TAX为每10,000美元的全额财产税率,PTRATIO为按镇划分的城镇师生比例,B为1000(Bk-0.63)^2其中Bk是城镇黑人比例,LSTAT为人口中地位低下者的百分比,MEDV为自有住房的中位数价值(单位:千美元)。以MEDV为因变量(预测目标),建立回归方程,预测房价,并评价模型性能。
3.关联规则挖掘
读取Case3.csv,试挖掘出支持度>=0.02,置信度>=0.35的关联规则。
4.梯度下降法实现多元线性回归(选做)
自行实现梯度下降法,实现多元线性回归中的参数计算。记录自己实现的梯度下降法的运算时间,与statsmodels中的方法进行比较。
5.Apriori算法实现关联规则挖掘(选做)
自行实现Apriori算法,实现关联规则挖掘。记录自己实现的Apriori算法的运算时间,与mlxtend中的方法进行比较。
三、实验过程及步骤
1.一元线性回归&多元线性回归
1.0实现思路
一元线性回归近似于用一条直线来拟合数据和结果,y = a·x + b。我们会希望数据的分布和拟合曲线之间的误差越小而且符合正态分布。
1.1基于Statsmodels.OLS的一元线性回归
在进行多元回归的时候需要将excel中多列参数值读到stark中,然后再调用相关函数。
1.2 DIY一元线性回归
定义矩阵乘法函数J(梯度下降函数)和对矩阵求导的函数dj,求导的结果决定了x的方向。
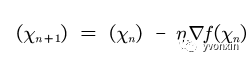
具体实现:使用numpy包中的dot函数实现点乘
2.相关分析
2.1将数据库中数据读成购物清单的格式

图二 格式转换
2.2遍历得到所有商品,放到C1中;
2.3假定支持度是0.2,计算每个商品的支持度(出现的频率),如果支持度超过0.2则放入L1层;
2.4将L1层中商品进行两两组合,得到C2,计算C2中每个组合的支持度,将支持度大于0.02的组合放入L2层;最终得到的L就类似是一个柜子,如下图所示,最后通过遍历可以得到支持度大于0.2的组合;
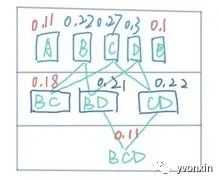
图三 实验结果效果图
四、实验结果及分析
1.出现的问题
·在使用自己写得多元线性回归递归的时候出现梯度越来越大的问题。
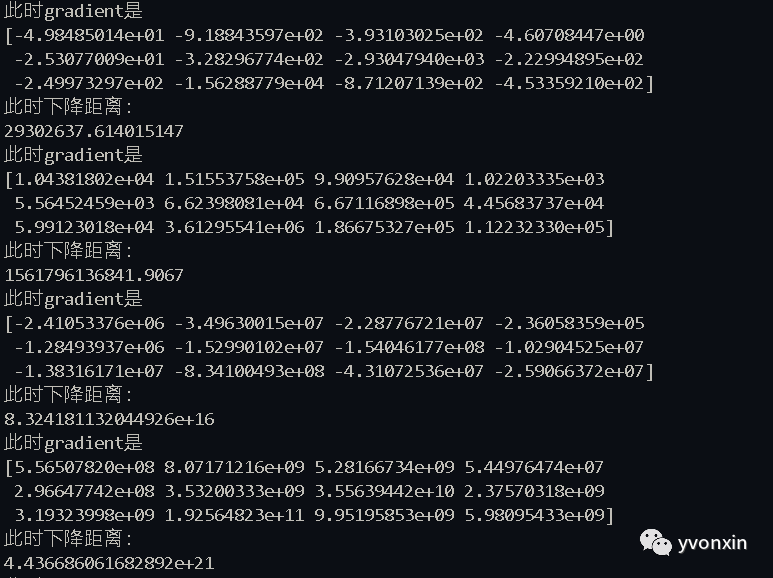
图四 每次迭代之后梯度反而上升
当我修改eta从0.01至0.000001后下降的数据恢复正常,在迭代后逐渐减小。

图五 在修改公式中的eta后数据恢复正常
2.结果时间对比

图六 结果时间对比
3.结果评估
在回归任务(对连续值的预测)中,常见的评估指标(Metric)有:平均绝对误差(Mean Absolute Error,MAE)、均方误差(Mean Square Error,MSE)、均方根误差(Root Mean Square Error,RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),其中用得最为广泛的就是MAE和MSE。
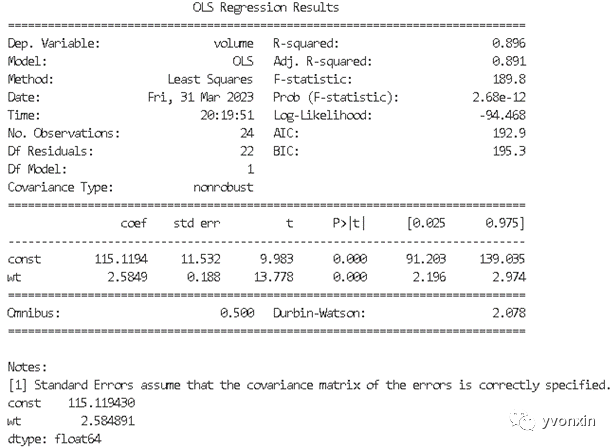
图七 一元线性回归summary
从图中我们可以看出样本数量(No.Observation)为24;
残差自由度 (DF Residuals,残差指的是实际观察值与估计值之间的差)为22,;
参数数量(DF Residuals)为1;
确定系数 (R-squared,说明估计的准确性“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好)为0.986,确定系数与SSR(Sum of squares of the regression,即预测数据与原始数据均值之差的平方和)和SST(Total sum of squares,即原始数据和均值之差的平方和)相关,R-squared = SSR/SST;
修正确定系数( Adj.R-squared)为0.981,这里修正确定系数公式为,p为模型中变量的个数,当引入新的变量时可以提高确定系数,我们引入修正系数相当于给变量个数的增加添加惩罚项。
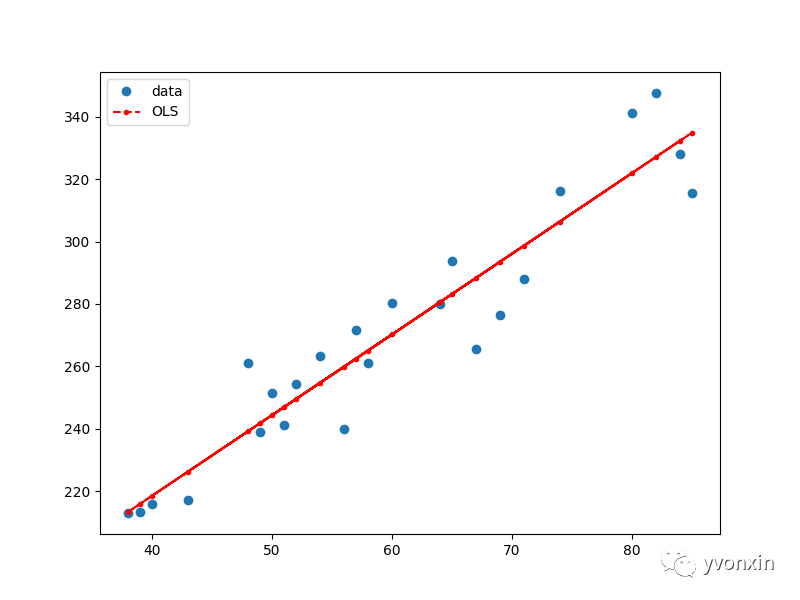
图八 使用Statsmodels.OLS的一元线性回归结果可视化
从图片中来看,Const 和 wt 分别意味截距和斜率。

图九 DIY一元线性回归结果
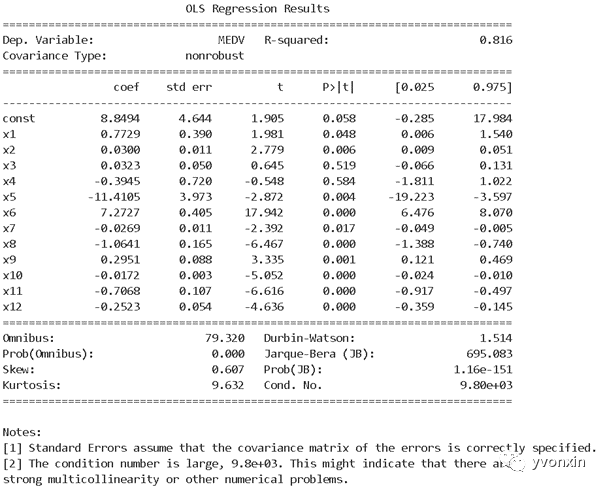
图十 多元线性回归summary

图十一 多元线性回归参数列表
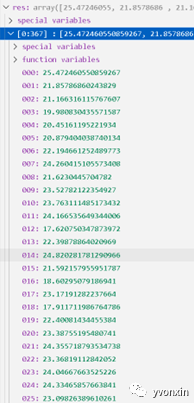
图十二 根据DIY多元数据模型预测出出来的房价(部分)

图十三 DIY多元数据评估指标
对比来看,DIY模型效果不是很好呀,这里的R2即左边多元线性回归summary中的R-squared,R2 是多元回归中的回归平方和占总平方和的比例,它是度量多元回归方程中拟合程度的一个统计量,反映了在因变量y的变差中被估计的回归方程所解释的比例。R2 越接近1,表明回归平方和占总平方和的比例越大,回归线与各观测点越接近,用x的变化来解释y值变差的部分就越多,回归的拟合程度就越好。
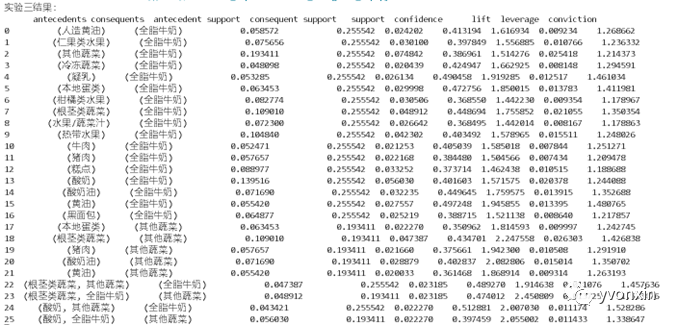
图十二 基于mlxtend.frequent_patterns的关联分析

图十三 DIY关联分析(部分)
-
python数据分析基础之使用statasmodels进行线性回归2020-06-19 0
-
基于用户兴趣导向的关联规则数据挖掘2009-08-26 588
-
关联规则挖掘在数据录入、校对系统中的应用2009-09-03 765
-
基于最大模式的关联规则挖掘算法研究2009-09-16 403
-
基于MapReduce的并行关联规则挖掘算法2018-01-10 1343
-
8种用Python实现线性回归的方法对比分析_哪个方法更好?2018-06-28 4437
-
用Python做几个表情包2019-02-11 5226
-
Logistic回归数学推导以及python实现2021-02-25 693
-
用Python写网络爬虫2021-06-01 705
-
在Anaconda中安装python包seaborn2021-09-18 664
-
用Python学习科学编程2022-03-09 576
-
python数据挖掘与机器学习2023-08-17 1356
-
Python SDK包的使用2023-10-30 781
-
线性回归模型的基础知识2023-10-31 572
-
python变量命名规则2023-11-23 1590
全部0条评论

快来发表一下你的评论吧 !

