

固态离子学基础知识:阻塞电极和浓度极化
描述
笔者在日常的科研以及与课题组同学讨论问题中发现,很多时候大家做的实验测量可以被描述为“测电阻”。简单的说,就是在一个样品(如离子/电子导电陶瓷块体或者薄膜)两边做上两个电极,然后加电压测试得到的电流。虽然这样的操作虽然看起来极为简单,但是由于我们经常面对的样品常常是所谓的“混合离子-电子导体 (Mixed Ionic-Electronic Conductor,下文简称MIEC)”,这样一个简单的操作背后的物理图像可能没有大家想象得那么简单。
本文就尝试给大家介绍一下,如果你的样品具有离子-电子混合导电(其实极为常见,甚至如不少导电聚合物、卤素钙钛矿材料都是混合导体),那测到的电导率意味着什么,在样品内部又发生了什么事情呢?
上述问题可以被抽象为图1所示,一个MIEC样品(例如很多能源转换与储存器件所用的材料等)放置于两个电极中间,施加一个电压(表示为 U ),我们会测到一个电流密度(用j表示)。
为了简单起见,我们把问题简化为一维,即假设电流密度在横截面上每一点都是相等的。这一假设在使用平行板状的电极(如一个陶瓷块体样品两边镀上电极)是较为容易满足的。在一维假设的基础上,我们把两个电极之间的样品厚度用L表示。
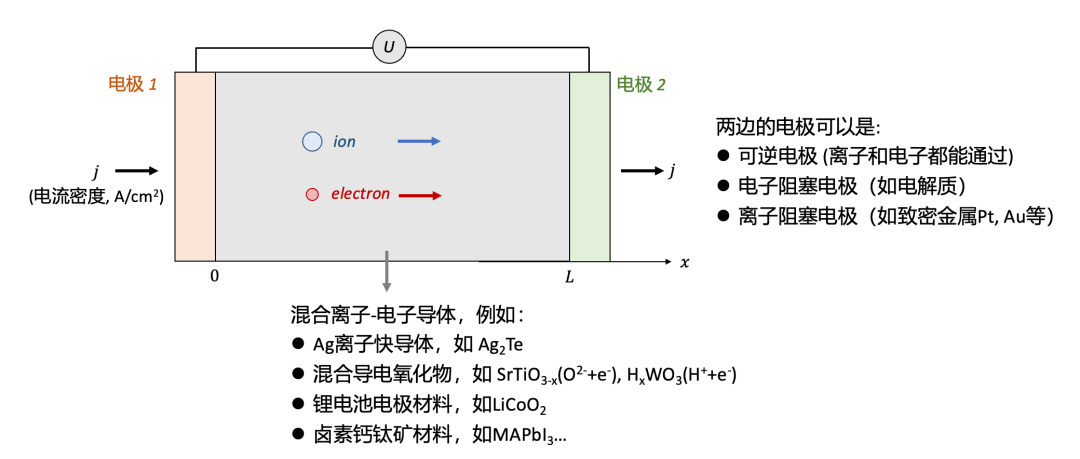
(图1.混合离子-电子导体的导电率测量:电极的选择)
首先我们需要解决的问题是电极的选择。根据选择的电极的不同,测量得到的电导率可能有极大的差异,而背后的物理化学过程也可能迥异。
一般说来,根据能通过的载流子种类的不同,电极可以分为三种:
可逆电极 (reversible electrode),即可以让离子和电子都通过的电极。因此,通过可逆电极的电流可以既有电子电流,也有离子电流。
对于不同体系,可逆电极的选取不尽相同。例如,对于锂电池材料(如LixFePO 4 , LixCoO2等),锂金属电极可以作为可逆电极。而对于高温下混合导氧离子和电子的氧化物材料,多孔的铂(Pt)金属电极可以作为可逆电极。
电子阻塞电极 (electron-blocking electrode),即只能让离子通过而电子无法通过的电极。如果用这种电极的话,通过电极的电流只能为离子电流。
常用的电子阻塞电极即为相应离子的电解质,如对于氧离子-电子混合导体,常用(Y,Zr)O2 (YSZ)作为电子阻塞电极。值得提起注意的是,由于外威廉希尔官方网站 导线只能让电子流过,所以在电子阻塞电极的两侧还需要用可逆电极来使得威廉希尔官方网站 完整。例如,如果用YSZ作为电极的话,还需要再加上多孔Pt作为电流收集层。
离子阻塞电极 (ion-blocking electrode),即只能让电子通过而离子无法通过的电极。
在日常的实验中,离子阻塞电极的使用非常普遍。例如,通过物理气相沉积(Physical Vapor Deposition,PVD)如磁控溅射或者电子束蒸发制备的致密的Pt或者Au电极,往往是离子阻塞电极。下文中我们将看到,使用离子阻塞电极将不可避免地带来MIEC内部的浓度极化。
从上面的讨论我们可以看到,如果想要回答测到的电导率的物理意义这一问题,我们首先需要反问自己用的电极到底是属于以上三类中的哪一类。电极的选择会完全影响测量得到的电导率的含义(离子电导/电子电导/全电导),而且对于瞬态(transient)过程和稳态(steady state)下MIEC中的离子浓度分布也有极大影响。
下文中我们将根据电极的不同分为几种情况讨论:
我们先讨论两边电极都是离子阻塞电极(如致密的Pt, Au等金属电极)的情况,这或许是实验中测量电导率大家最常遇到的电极情况。而对于电子阻塞电极,我们会发现情况与离子阻塞电极有相似之处,我们还将讨论一端阻塞电子一端阻塞离子的情况。我们最后讨论一端是可逆电极的情况,以及所谓的Hebb-Wagner法测量电导率。希望本文对于大家厘清一些固态离子学的基本概念有所帮助。
一、离子阻塞电极:物理图像
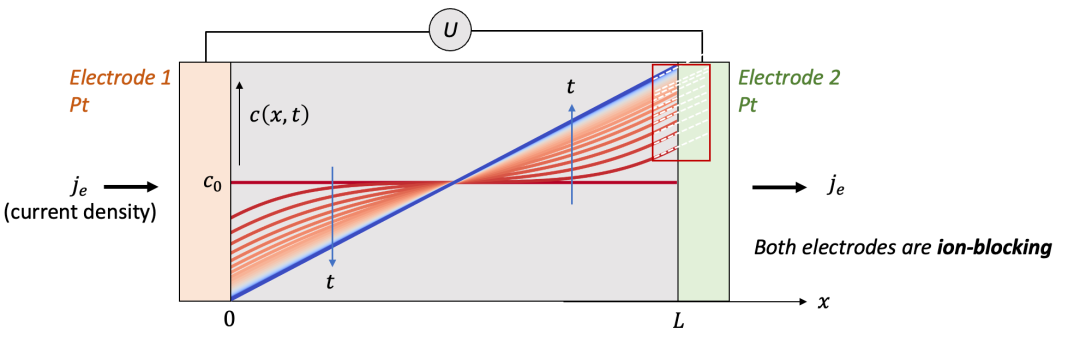
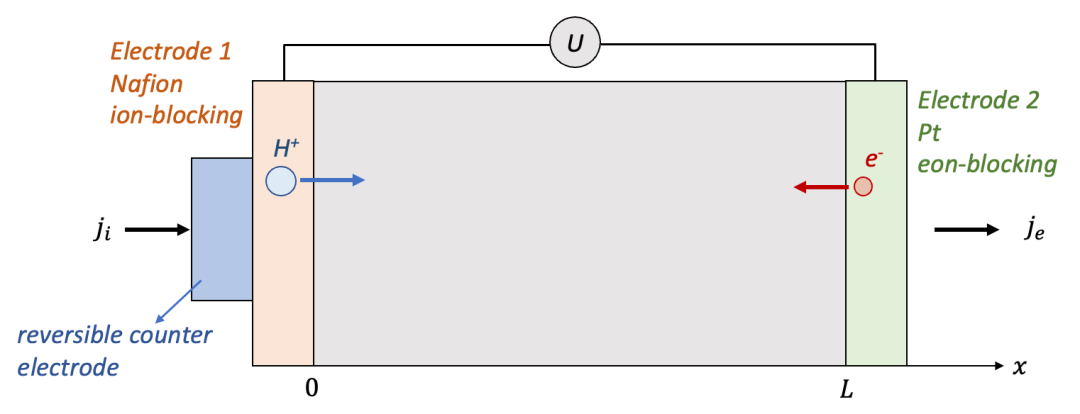
我们首先讨论两边电极都是离子阻塞电极的情况,如图2中所示。为了讨论方便,我们用氢化(hydrogenation)的氧化钨(HxWO 3 ,同时具有质子H^+^和电子e^-^导电)作为MIEC的一个例子。
两边的电极为致密的Pt薄膜,意味着只能让电子通过而质子无法通过。可以想象,如果在两端电极加一个电压,离子和电子都会开始移动,但是两端的电极只能让电子通过,意味着通过电极的电流密度仅仅由电子电流构成。
我们想知道的是样品中空间上每一点的化学组成(即H的含量,HxWO3中的x)随着时间怎么变化,以及怎么把两端加的电压U和H的浓度变化联系起来。
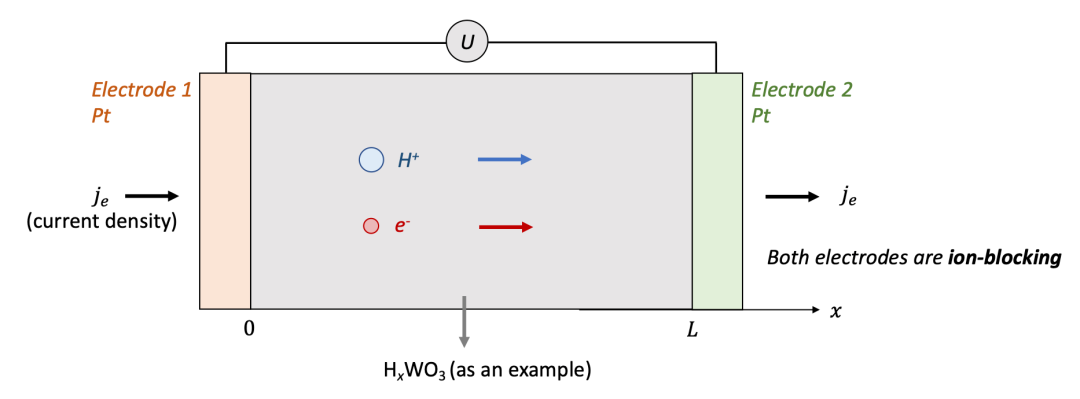
(图2.离子阻塞电极的物理图像)
根据离子和电子的漂移-扩散(Drift-diffusion)输运方程(细节可以参看我们以前的公众号文章:WESTON OpenCourse | 第三章:离子输运的宏观图像与电化学势),可以把电子和离子的电流表示用以下方程表示:
电子电流:
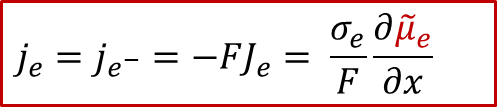
其中je是电子电流密度,而Je是电子的通量,σe代表电子导电率,最后一项位电子的电化学势的梯度,注意电子的电荷 z e - 为+1)
离子电流:
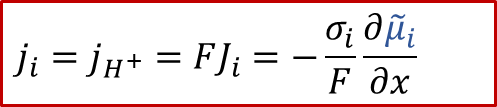
质子的电荷 z H + 为+1,σi代表离子导电率
由于离子电流为零(两侧是离子阻塞电极),所以我们有:

上面公式意味着,由于离子电流为零,MIEC中每一点的离子的电化学势都一样(梯度为0),而我们知道,对于任意一个电化学系统,两侧电极能测到电压,说明两侧的电子的电化学势不同,即:
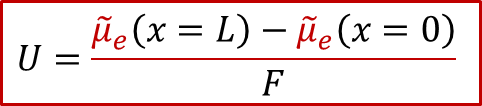
也就是说,两侧施加的电压,造成了两侧电子的电化学势的不同,而根据MIEC中局域每一点的电中性条件(我们后面会详细讨论为什么电中性条件是必要的),我们有:

再结合上面电压的表达式,我们最终得到:

可以看见,外加的电压最终转换为了H的化学势μ在MIEC两端的差值,也就是说,外加的电压造成了MIEC内部的H的浓度的不均匀,这也就是所谓 **浓度极化 ** (concentration polarization)。如果我们假设外加的电压不是很大,并且MIEC满足稀溶液假设(dilute limit),那么我们可以得到:
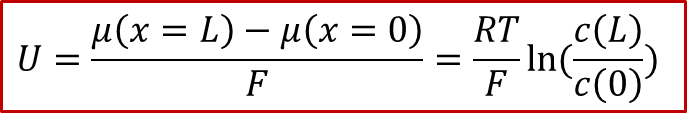
由于图2所示的体系有中心对称性,中心( *x * = L/2)处的浓度将保持为原有浓度,我们记为,我们同时把两边的浓度差值记为,那么我们可以得到电压和浓度差值的关系:
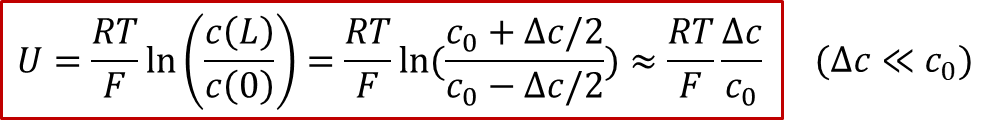
由此可见,由于两边的电极是离子阻塞电极,施加的电压最终(在稳态下)会转化为两侧的浓度差,因此电压的本质是所谓“Nerstian”,即类似能斯特方程中的浓度项。
值得指出的是,上述讨论可以类比到电子阻塞电极,唯一不同的是如果两边是电子阻塞电极的话,电子(而非离子)的电化学势每一点都相等,两边的电压差别变为用离子的电化学势差表示。
二、电中性条件的必要性
在上面的讨论中,很重要的一点是样品中每一点都保持电中性,即带正电的质子和带负电的电子在每一点的浓度必须相等(浓度等于中性的 H 的浓度)。
粗看起来或许这有点违背直觉。笔者跟课题组的同学们讨论的时候,很多同学的第一反应是:加一个电压,带正电的质子和带负电的电子应该向相反方向移动从而造成所谓的“电荷分离”。
我们这里必须厘清一个非常重要的概念,即在MIEC中,除非在界面处等特殊情况,否则电中性的条件必须满足,因此电子和离子的移动必须同时发生,即所谓的化学扩散(ambipolar chemical diffusion)。
下面我们就来看看为什么电中性条件必须满足,或者说在一个较大的空间尺度上不满足电中性会有什么后果。
泊松方程(Poisson’s equation)告诉我们,静电势的二阶导数和净电荷(正的减去负的)相关,如以下公式表示:
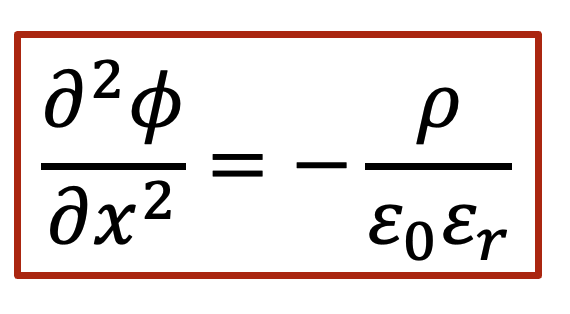
我们就根据泊松方程做一下所谓的“back-of-the-envelope calculation”,我们假设电中性条件如果不满足,我们假设样品里面有0.1 mol/L的正电荷(比如质子浓度相较电子浓度高出了0.1 mol/L),那么根据泊松方程,静电势的变化ΔV可以表示为(假设相对电容率为10):
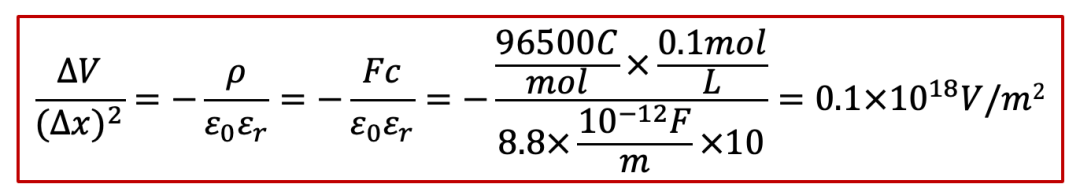
其中Δx是不满足电中性的区域的长度(我们还是假设一维的情形)。那么,如果我们改变Δx,会有什么后果呢?如果我们计算ΔV和随之而来造成的能量,我们可以得到下表(假设样品横截面积为1 cm^2^):

我们可以看见,如果把不满足电中性的区域的尺度限制在纳米级别,造成的电势差已经达到1 V,这其实也就是我们经常见到的双电层的情形,还是比较合理的。
但是如果不满足电中性条件的区域超过纳米尺度,事情就开始变得不合理了。如果尺度达到1 μm,电势差已经达到MV级别,已经相当大了。而如果我们再极端一点,如果把尺度拉大到1 mm,那么相对应的能量已经远远超过1 TNT当量所对应的能量,这简直太可怕了!
当然上面的极端情况显然不能在我们测量的MIEC样品中存在,上面的例子只是告诉大家,在绝大多数情况下,如果MIEC的载流子(离子+电子)浓度较高,MIEC的块体(bulk)中都是满足电中性条件的,只有在界面附近(或者晶界等“Extended defects”)有可能不满足电中性。
这样说明,在MIEC中的化学扩散(化学计量比或者浓度的变化)必须是离子和电子的协同扩散,而扩散较快的物种必须“等待”扩散较慢的物种从而保持局域的电中性。而回到我们上面两边都是离子阻塞电极的例子,每一点都满足带正电的质子和带负电的电子浓度相等,所以其实电中性的H的浓度的变化也是化学扩散行为,由H^+^和e^- ^的协同扩散造成。
三、化学扩散和菲克定律:
解析浓度随时间变化
上面的讨论中,我们明确了两端的电压U和两端的浓度差的关系,但是我们还想进一步知道施加电流/电压过程中样品中空间上每一点的浓度变化随着时间演化的规律。
上文提到,两端是离子阻塞电极的情况下,实际上样品中的浓度变化与化学扩散的过程类似(由于电中性条件)。那么我们其实可以通过求解一个扩散方程来得到浓度( c(x,t) ,表明浓度是空间位置0< x
下面我们就简单讲讲如何求解 c(x,t) ,首先我们假设在两侧施加一个恒定的电流密度 j ,也就类似真实的实验过程中我们用恒流源施加一个恒定电流,然后测量两端的电压U的变化。根据菲克第二定律,我们有:
上式中**D^δ^**就是所谓的化学扩散系数,具体化学扩散系数的定义以及影响因素,可以参看我们另外一篇公众号文章:WESTON OpenCourse | 第五章:扩散系数的类型及化学扩散。
为了求解以上的扩散方程,我们当然要明确体系的初始条件(t = 0的情形)和边界条件( *x * = 0, L 的情况)。初始条件比较好解决,没有外加电流之前,MIEC内部各处的H的浓度应该都是初始浓度 c0 ,即:
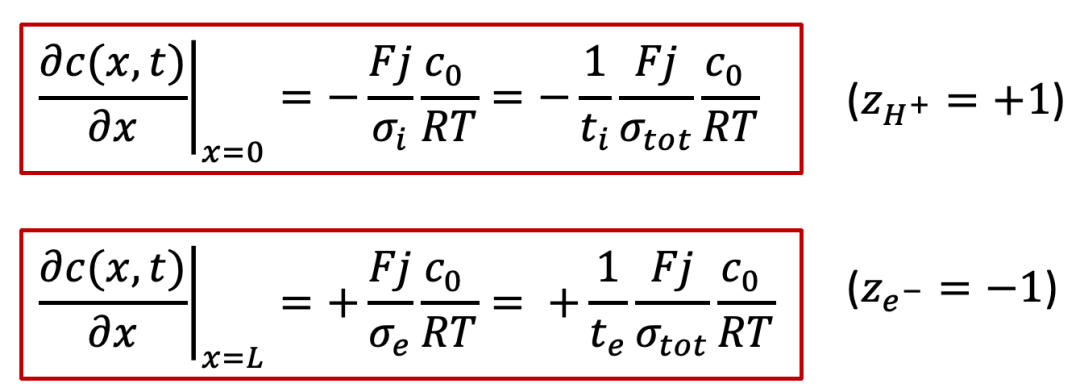
而边界条件较为复杂,还是要从两边的电流入手,由于两边的电流都是电子电流(离子被阻塞),而且是一个恒定值 j ,我们有:
注意以上的公式只对于x = 0, L成立,我们可以反求出边界条件:
有了以上的初始和边界条件,我们就可以求解扩散方程了。这里我们还需要假设所加的电流密度j比较小,引起的浓度变化不会改变 D^δ^ ,否则方程解起来非常困难(只能数值解)。
在假设*D^δ^*恒定的基础上,以上方程有解析解,如下所示(参考Yokota, J. Phys. Soc. Jpn., 1961):
其中函数Φ有以下的表达式:
而 c(x,t) 表达式中有一个 τ^δ^ ,其实这一项就是跟化学扩散相关的时间常数,我们知道扩散常数的单位是m ^2^ /s,因此*τ^δ^跟L^2^*成正比,即:
上面的解析解比较复杂,但是如果把x = 0, L带入,不难看出这个解为什么成立。笔者这里强烈建议各位读者动笔演算一下,相信能增加不少理解。
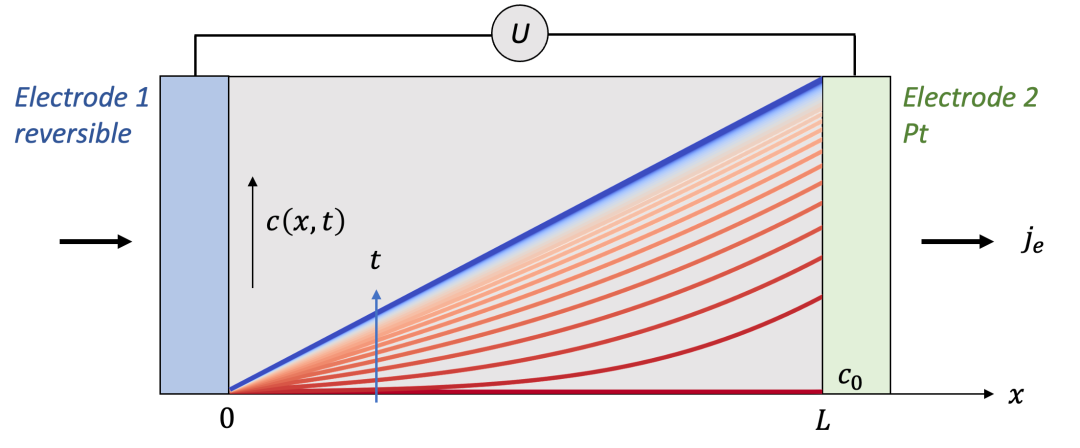
如果我们把解析解随着时间t的演化画出来,我们就能得到如图3中所示的一系列曲线。
(图3.MIEC中空间上每一点的浓度随着时间的演化规律)
我们通过观察这些曲线,可以发现几个有意思的现象:
我们可以发现在样品的边界(x = 0, L,即图3中右边画红框处) c(x, t) 的斜率(导数)在不同时间t都是一样的。这是因为我们假设的边界条件是恒定的电流密度 j ,因此两个边界上浓度随着空间的导数都是不随时间变化的。
我们可以想象一下,如果达到稳态(steady state,即t趋于无穷时的状态)时,样品内部的浓度分布应该是什么样的呢?
稳态下的定义是浓度不再随时间变化,即:我们可以看到,由于浓度不再随时间变化, c(x, t) 对于x的二阶导数应该为0,所以c(x, ∞)在空间上分布应该是一条斜线(线性分布),如图3中蓝色线条所示。
由于我们固定恒定电流密度 j ,由图3可以看见,在瞬态(transient state)的演化过程中,两侧的浓度差不断变大,这也就意味着,两端测到的电压U也是时间的函数(表示为 U(t) )。
如果我们还是假设体系满足稀浓度条件(对于MIEC,即缺陷-缺陷相互作用可以忽略不计),那么我们其实可以计算出电压 U(t) 的演化规律,由于:
而通过 c(x,t) 的解析解,我们可以算出两端的浓度差Δc随着时间的变化,所以我们最终得到:
从上面的公式我们可以看出,两端测到的电压随着时间是变化的。如果我们足够有耐心等到稳态(t趋于无穷),可以得到:
上面的公式其实就是欧姆定律( E = IR )的另外一种表现形式(注意j的单位是A/m ^2^ ),也表明由于用了阻塞电极,稳态下测到的电导其实就是只有电子电导σe的贡献。而如果我们没有那么耐心等无穷长时间,那么当t >> *τ^δ^*时,我们也有:
实验上,我们可以有以下线性关系:
也就是说,我们按照上面做ln(U(t)-U(∞))和t二者之间的线性关系图,根据斜率就可以求出 τ^δ^ ,从而进一步推算出化学扩散系数 D^δ^ ,这也提供了一种测量MIEC的化学扩散系数的电学方法。
四、电子阻塞电极+离子阻塞电极:
电化学储能原理
上面我们详细了讨论两边电极都是离子阻塞电极的情形,那么一个自然的想法是,如果把一边换为电子阻塞电极(如图4所示),会有什么样的不同呢?
我们还是以HxWO3为例,右边还是用离子阻塞的致密Pt电极,左边换为可以让质子通过而阻塞电子的电极如Nafion等(前文也叙述过,最终外威廉希尔官方网站
还是电子导通,所以需要一个可逆电极共同和电子阻塞电极使用)。
(图4.电子阻塞电极(左)+离子阻塞电极(右)的情形)
跟上面的讨论一样,我们还是希望理解MIEC样品中空间上每一点的H的浓度随着时间如何变化。与两端都是离子阻塞电极的情形一样,电中性条件也是适用的,所以本质上还是求解扩散方程。同时,初始条件也没有变化,即一开始样品中每一点的浓度都是初始浓度 c0 ,唯一有变化的是边界条件。
此时两边电极不再对称,我们仍然假设外加一个恒定的电流密度j,但是注意电流密度在左侧电极变为只有离子电流 ji ,而在右侧电极变为只有电子电流 je ,据此我们可以写出边界条件:
注意:上面符号的不同是由于质子和电子所带电荷相反。
而且,我们可以观察到,在两个电极处的边界条件除了符号相反,其实是相差了离子和电子的迁移数,迁移数的定义如下:
结合上面的初始和边界条件,扩散方程也是有解析解的,但是实在是太过于复杂,笔者建议读者参考相关文献(如Preis and Sitte, J. Chem. Soc., Faraday Trans., 1996, 92(7), 1197-1203)。
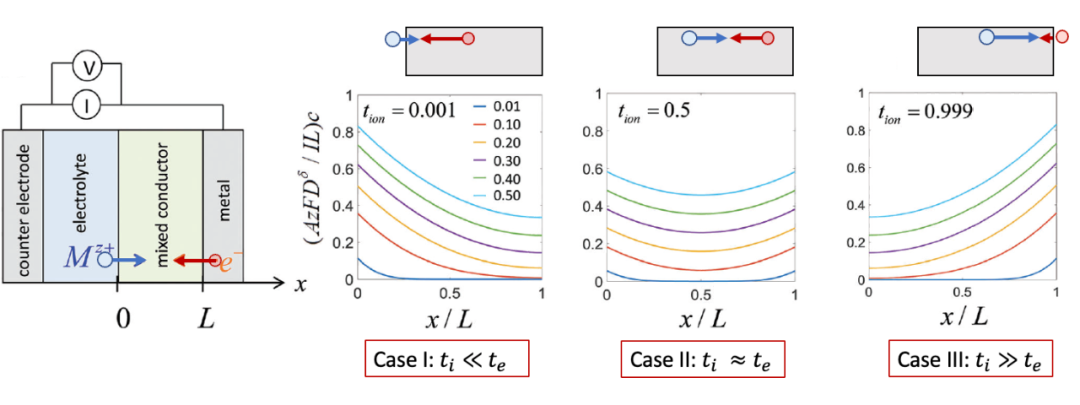
我们这里想定性讨论三种情况,如图5所示(摘自Usiskin and Maier, PCCP, 20, 16449)。
(图5. 根据离子迁移数区分的三种不同的化学扩散情形)
adapted from Usiskin and Maier, PCCP, 20, 16449
电子迁移数te远远大于离子迁移数t~i ~的情形。
如图5中Case I所示,我们想象一下,由于这种情况下电子“跑得快”,电子电导远远大于离子电导,因此化学扩散首先从左边的界面,即电子阻塞电极处发生。
从上面的边界条件也可以看出,由于ti ~ ~ << te ,左侧边界的通量(正比于浓度随空间的导数)的绝对值是要远远大于右边的。而浓度分布随时间的演化也在图5中所示,可见左侧的浓度增加速度要远远快于右侧,这也证明化学扩散或者浓度变化从左侧开始。
电子迁移数te与离子迁移数ti差不多,即“电子和离子跑得差不多快”。
在这种情况下,化学扩散从两边同时发生。由上面的边界条件也可看出,这是两边的通量的绝对值相等。浓度随时间演化的情况如图5中Case II所示。
离子迁移数ti远远大于电子迁移数te的情形( t~i ~ >> te )。
如图5中Case III所示,这时候跟上述第一种情形反过来,由于这时离子跑得比电子快,所以化学扩散过程反而从右侧界面发生。
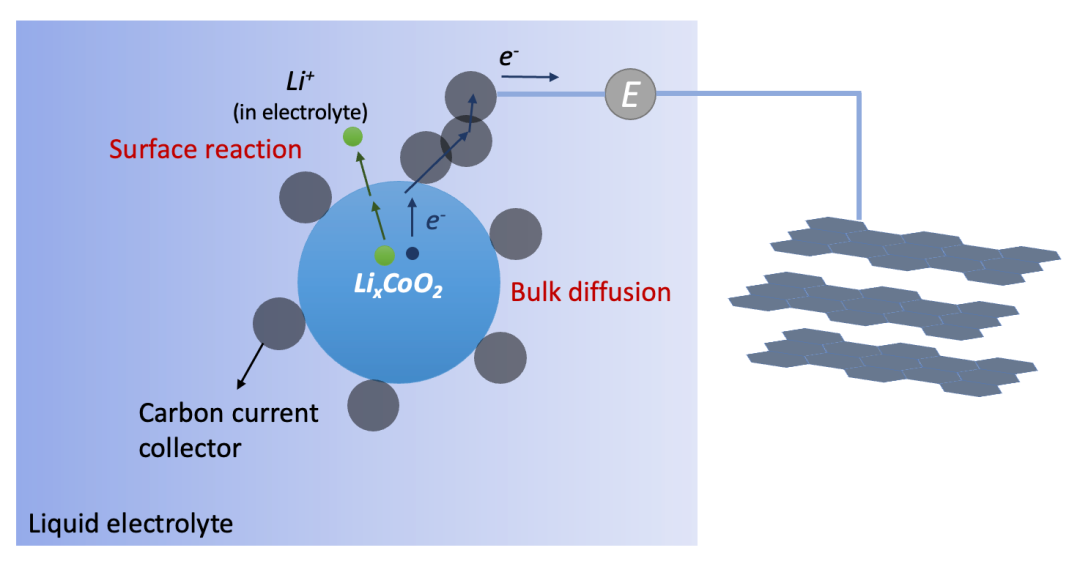
其实上述过程,即由离子阻塞电极和电子阻塞电极共同存在的化学扩散情况在实际应用中非常普遍,最典型的就是锂离子电池电极材料的充放电(离子嵌入intercalation)过程,如图6所示。因此,这样的过程其实是所有电化学储能的基础,因为涉及到把一个中性的物种(例如Li)拆分并分别输运(例如 Li^+^ 和 e^-^ )的过程。理解离子/电子阻塞电极因而对于理解电化学储能的物理图像有着非常重要的作用。
(图6.锂电池正极材料的充放电过程)
其实也是由离子阻塞电极(集流体)和电子阻塞电极(电解液)共同驱动的化学扩散过程
除了电化学储能,其实这种阻塞电极的配置也非常普遍。我们举另外一个关于有机半导体聚合物的例子。研究者发现其实很多有机导电(或者半导体)聚合物都是离子-电子混合导体,而离子电子的协同扩散(其实就是化学扩散)会影响这些有机聚合物的导电率的变化速度,同时也会影响其他物理性质比如透过率等。
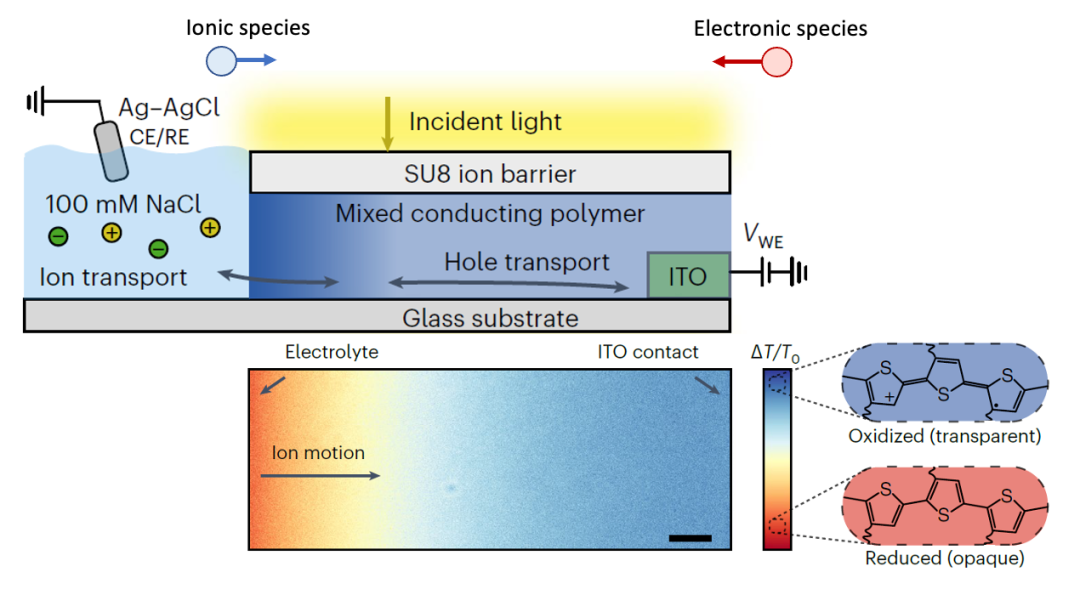
今年最新发表在Nature Materials上的一篇文章,其实就是用了离子阻塞电极+电子阻塞电极研究了化学扩散过程(Keene et al., Nat. Mater. (2023),如图7所示)。
(图7.导电聚合物中化学扩散对于光学透过率的影响)
adapted from Keene et al., Nat. Mater. (2023)
上图所用的测量方法,其实就跟图4中一样,左边是电子阻塞电极(电解质),右边是离子阻塞电极(ITO电极)。在施加一个电压以后,电中性物种(离子+电子)开始从左边界面的化学扩散行为,改变电中性物种的浓度,从而改变导电聚合物的光学透过率。
这篇文章的作者们还详细讨论了什么情况下化学扩散从左边界面开始(图5中Case I),什么情况下从右边界面开始(图5中Case III)。所以其实很多材料体系,看似完全不同,其实内在的物理化学规律是一样的,这也显示出固态离子学知识的泛用性和重要性。
五、可逆电极:Hebb-Wagner法测试电导
最后一部分我们来讨论可逆电极的情况,我们还是以前面的两边都是离子阻塞电极出发,只是这时候我们把左边的电极换为一个可逆电极。
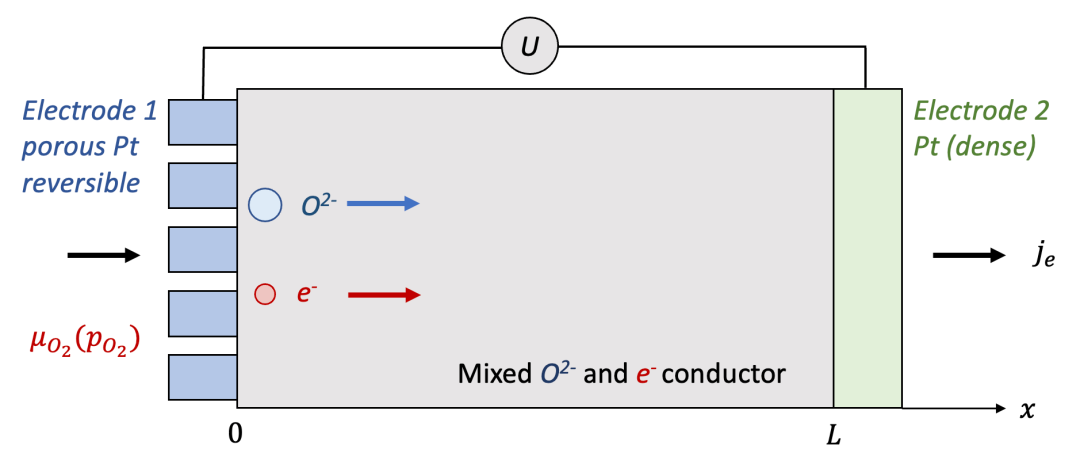
这里我们以混合氧离子( O^2-^ )和电子( e^-^ )导体为例,如图8所示。对于高温下混合导通氧离子和电子的氧化物混合导体(例如(La,Sr)CoO3-x,(La,Sr)FeO3-x等,甚至对于电解质YSZ等都有一定但是非常小的电子电导率),致密的Pt电极可以认为是离子阻塞电极。而多孔Pt电极由于可以允许表面的氧交换反应,因而可以认为是可逆电极。
(图8.左边为可逆电极,右边为离子阻塞电极的情形)
以氧离子+电子混合导体为例
我们还是想知道电中性的物种(这种情况下是 O ,即 O^2-^ - 2e^-^ )的浓度分布随着时间的变化趋势。读者可能已经猜到了我们的套路,在外加驱动力不大的情况下,本质上还是求解化学扩散方程(同时假设化学扩散系数*D^δ^*为定值)。当然,跟前面唯一的不同在于可逆电极处的边界条件的确定。其实结论非常简单,在可逆电极处的浓度会保持初始浓度 c0 ,即:
为什么呢?这是因为可逆电极因为可以同时导通离子和电子,因此平衡条件要求可逆电极的电中性物种的化学势(比方说,对于氧化物就是氧电化学势 μO )与初始条件下c0对应的化学势相等,因此在可逆电极处,浓度将保持不变,始终等于 c0 。
比如图7中所示氧化物的例子,通常我们实验中会把氧化物在一定的高温下与外界的氧分压(pO 2 )达到平衡,这时左边的多孔Pt和氧化物的μO会达到相等。而后续在施加电流电压的过程中,左边可逆电极处由于还是跟外界的氧分压pO2达到平衡,因此边界条件要求此处氧的浓度保持初始浓度。
而右边的离子阻塞电极处,边界条件与上文讨论中仍旧相同,即有:
如果我们按照以上的边界条件求解扩散方程,可以得到如图9中所示的浓度分布演化规律 c(x,t) 。足够细心的读者可能已经发现,这种情况下的 c(x,t) 其实与图3中所示的 c(x,t) 的右半部分一样。这也是很合理的,因为如果两边都是离子阻塞电极,由于对称性,x = L/2处得浓度会保持在初始浓度 c0 ,与可逆电极处一样。因此如果把一边改为可逆电极,相当于从把两边都是离子阻塞电极得情况从中间“切开”,再在x方向上拉长到原来的两倍而已。
(图9.左边为可逆电极,右边为离子阻塞电极情形下的浓度分布时间演化规律)
到现在为止,我们为了求解扩散方程,都假设外加的电流或者电压比较小,从而认为化学扩散系数D^δ^以及离子和电子的电导,即σi和σe都在样品中各点都基本保持不变。在这种情况下,扩散方程的解析解比较容易获得。
下面我们放宽这一限制,在图8所示情况(左边可逆电极,右边离子阻塞电极,样品为氧化物材料)下,我们施加一个较大的电压U,大到足够引起样品中空间上各点的电子(或离子)电导不一致,我们会有什么发现呢?
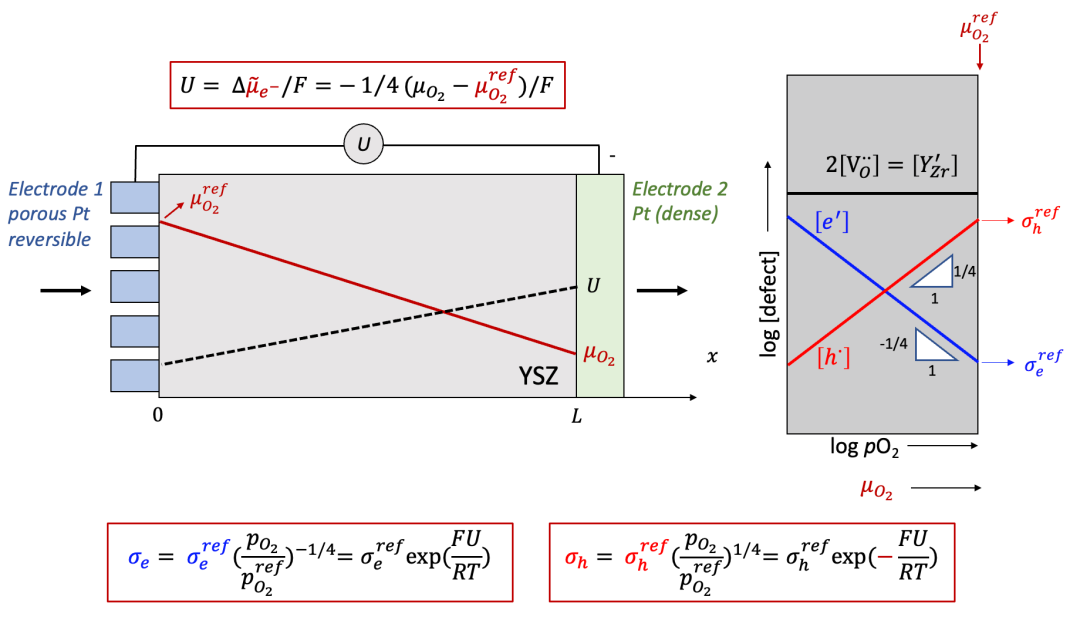
这里我们以很多读者非常熟悉的固体氧化物燃料电池电解质YSZ作为例子。YSZ虽然是离子导体(ti非常接近于1),但是也有一定的电子电导,相较于离子电导低很多,如图10中右侧Brouwer图所示(如果对于Brouwer图不太熟悉,请看我们之前的公众号文章)。
(图10.Hebb-Wagner法测试YSZ的电子电导:Brouwer图)
如果我们在右侧的离子阻塞电极和左侧的可逆电极之间加上一个电压 U ,而且U比较大,会发生什么呢?我们可以通过以下几点分析:
由于右边的电极是离子阻塞,所以得到的电流还是电子电流,即离子电流为零,所以氧离子的电化学势梯度也为0,那么我们通过电中性条件可以得到:
由上面公式可以看出,施加的U越大,样品右侧的氧的化学势偏离左侧可逆电极处的参比氧化学式(由初始氧的浓度决定)就越大,如图9中所示。
由上面讨论可以看出,施加电压以后,样品中每一点的氧的化学势(或者等效氧分压)不同,而如图10中的Brouwer图所示,YSZ的总电子电导由电子和空穴共同组成,而电子和空穴的浓度都是氧的化学势的函数,可以表示为:
而空穴电导为:
有了以上两个观察,我们最终关心的是施加一个电压U后得到的电子电流密度如何计算。
由于电子电流由电子和空穴共同决定,因此我们需要计算电子和空穴电导的共同贡献。注意电子和空穴电导在空间上每一点都是不一样的,我们可以通过积分来计算,即从下面公式出发:
我们有:
又由连续性条件,每一点的电流密度je都是一样的,因此上面公式左边就等于 j~e ~L ,因此,我们有:
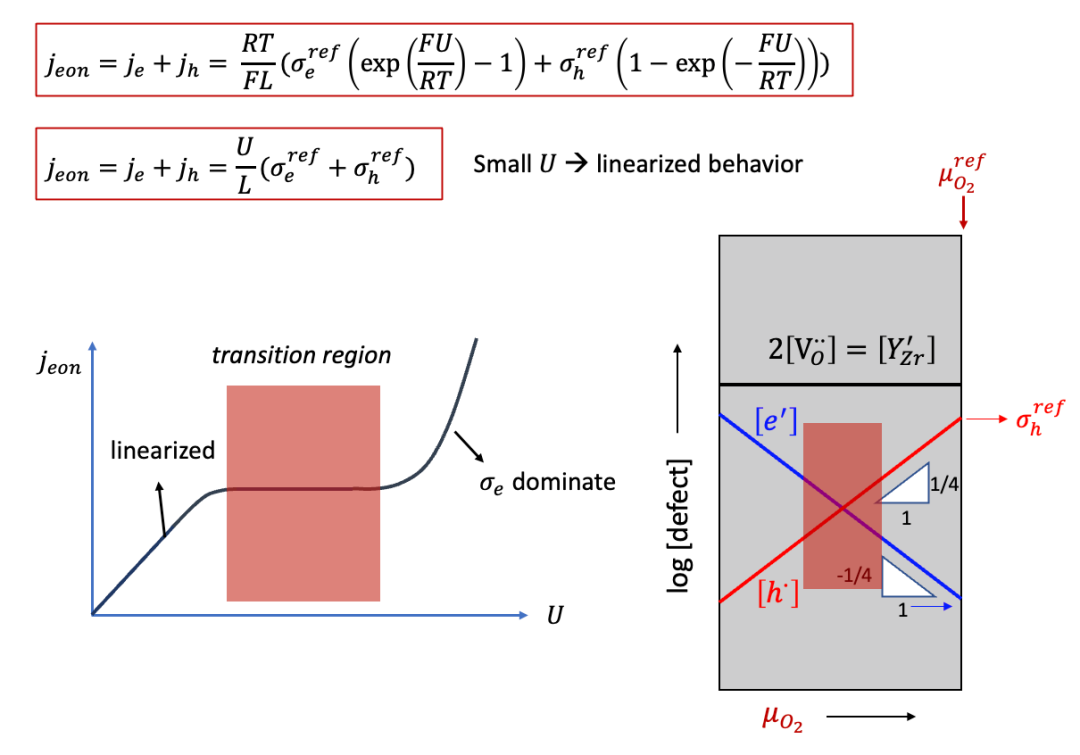
空穴电导与上面的计算类似,所以总的电子电流密度jeon为:
上面的公式会有几个很有趣的结果,比如,如果U比较小,那么我们知道exp(x)~1+x,我们可以得到:
这其实与上文中两边都是阻塞电极的情形类似,即在比较小的U的情况下,可以认为电子电导是不随U变化而变化的,因此U和j之间成线性关系,满足欧姆定律。
而如果U并不是很小,则U和j的曲线如图11中所示。有趣的是,j在一定范围内会基本不怎么增长,因为这时候进入了Brouwer图中的所谓转变区域(transition region),即从空穴导电占主导向电子导电占主导转变。进一步增加 U ,则进入了电子导电占绝对主导的区域(空穴导电此时低了很多),而j基本上随着U呈指数增长。
(图11. Hebb-Wagner法测试YSZ的电子电导:电压和外加电流之间的关系)
上述测量电子电导的方法,即一边是可逆电极,一边是离子阻塞电极的测量,一般被称作Hebb-Wagner方法(最早由M. H. Hebb和C. Wagner两位科学家分别独立提出,因此得名)。
可以看出,这种方法是一种非常高效的测量电子电导随着电化学势变化趋势的方法,因为只需要改变外加的电压U就可以,而不用真的通过化学方法改变电化学势。因此Hebb-Wagner方法在混合离子-电子导体的研究中得到了广泛的应用。
当然,上面一个问题是需要知道电子(空穴)电导与化学势之间的关系(即Brouwer图中的斜率),这一限制可以放宽到仅仅假设一个power law,相关更深入的讨论可以参考郭新教授和Maier教授的经典论文(Guo & Maier, Solid State Ionics 130, 267–280 (2000))。
六、总结
笔者希望读者通过阅读本文,能知道测量MIEC的电导率其实绝非易事(highly non-trivial),所以下次如果再接触到混合离子-电子导体,读者在施加一个电流(或电压),测到一些数据后,如果能反问自己:我测到的数据到底意味着什么?带着这个问题再来读一遍本文,那笔者认为这篇文章的意义就达到了。这里我们简单总结一下本文的一些知识点:
测试电极的选择非常重要。
根据是否会选择性地让某种载流子通过,电极可以分为可逆电极(只导通离子+电子),离子阻塞电极(只导通电子)以及电子阻塞电极(只导通离子)。对于不同的MIEC体系,我们需要知道选择的电极是属于上述三种里面的哪一类。
电中性条件在MIEC的体相(bulk)中一定满足,即便是有电压/电流的情况下。这是后面求解化学扩散方程的基础。
对于两端都是离子阻塞电极的情况,测试得到的电流是电子电流,但是只有等到稳态下测到的电导率才是真实的电子电导率。如果外加的电流/电压不太大,则在稳态下电中性物钟的浓度分布是线性的。这是这种情况下浓度极化的规律。
对于一端阻塞电子一端阻塞离子的情况,需要分析电子和离子的迁移数的相对关系。这种情况也是电化学储能的基础。
对于一端是可逆电极,一端是离子阻塞电极的情况,这时我们可以施加一个较大的电压来调控化学势分布,从而得到电子电导随着化学势变化的规律。这一方法被称作Hebb-Wagner测电导率法。
七、 后记:一点历史
正如本文开头所说,萌生写这篇文章的想法是因为跟课题组的同学们讨论实验结果和实验设计。虽然之前笔者读博士阶段陆陆续续看过这方面的内容,但是为了写这篇文章又去把一些“古早”文献看了一些。基本所有文献都会提到Yokota在上世纪五六十年代的开创性的工作,如图12所示。
这两篇60多年前的文章中基本涵盖了本文的绝大部分讨论,所以还是推荐大家去看看这些文献(都发表在Journal of the Physical Society of Japan这一日本“国产”期刊上)。
这里再多说一句,我们处于一个信息和文献都呈爆炸式增长的阶段,但是“溯源”我觉得还是很有意义的。
笔者读博士的时候,有一次参加一个会议,一位Keynote speaker在报告时候说“Every 30 years, we need to do the same things again, since the last generation of practitioners have already retired. (并非原话,不过大概是这个意思)”。听众听完爆笑,不过可能大家都略有所思。我们的研究中不断面临着新的问题,但是知道前人做了什么,以及必要的时候知道很多细节,对于我们向前走和训练学生也是非常重要的吧:)
(图12.横田伊佐秋(Isaaki Yokota)先生
在20世纪50、60年代的两篇论文和热力学著作)
笔者在网上并没有找到太多关于横田伊佐秋(Isaaki Yokota)这位学者的生平,只知道他是位凝聚态物理学家,1916年出生,1998年去世,学术生涯基本都在日本新泻大学度过,也写了不少重要的教科书(比如热力学(图12)和统计物理等)。如果哪位读者了解更多这方面的历史,还请不吝赐教。
审核编辑:汤梓红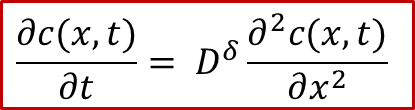
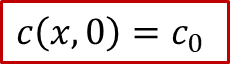
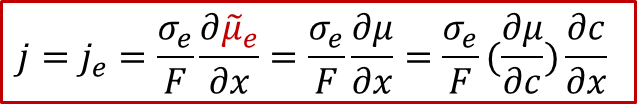
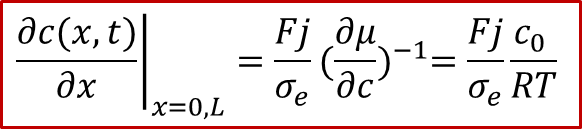
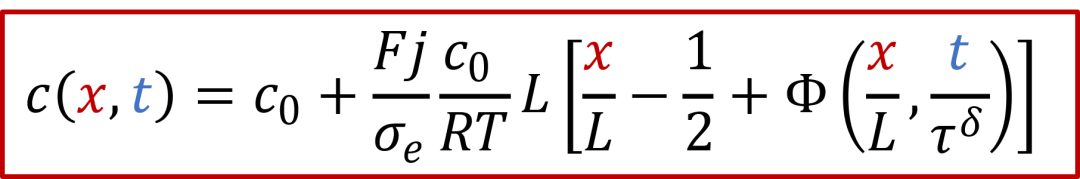
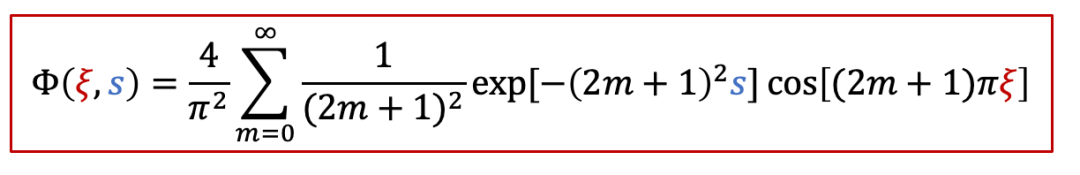
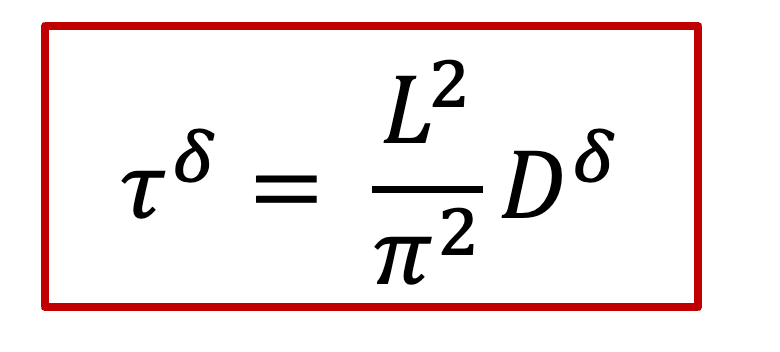
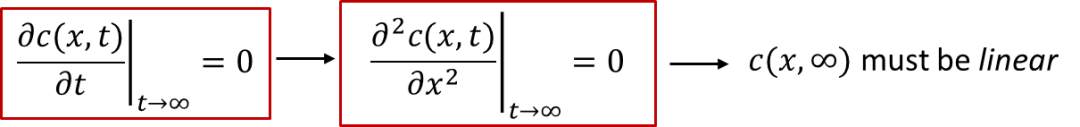
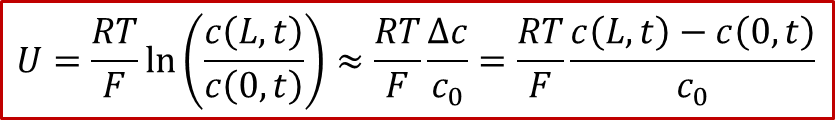
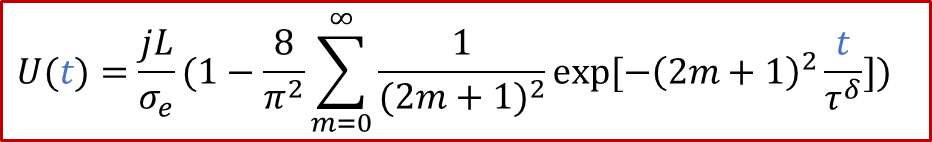
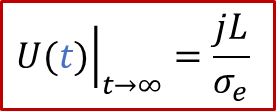
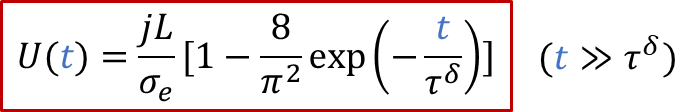
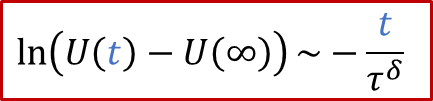
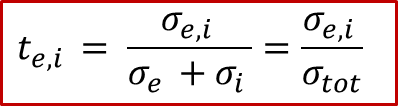
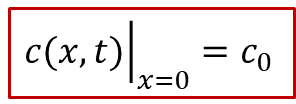
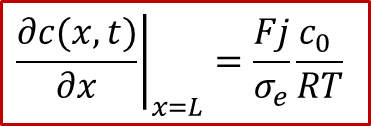
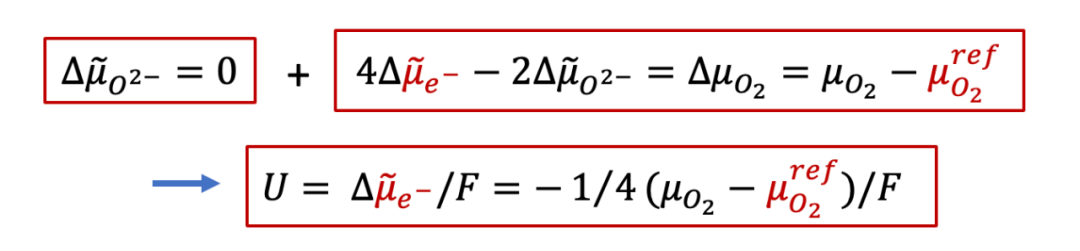

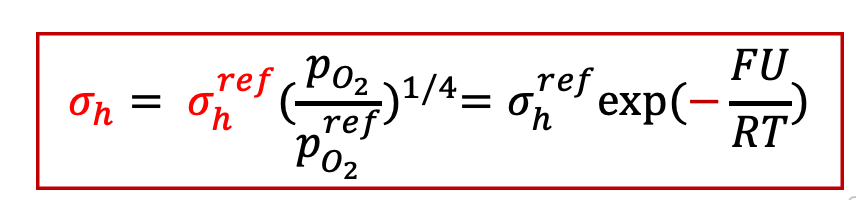
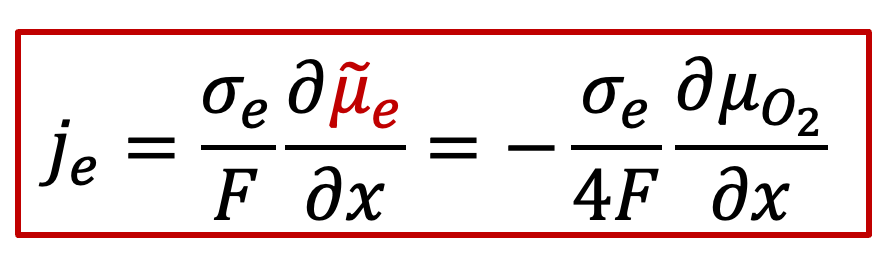
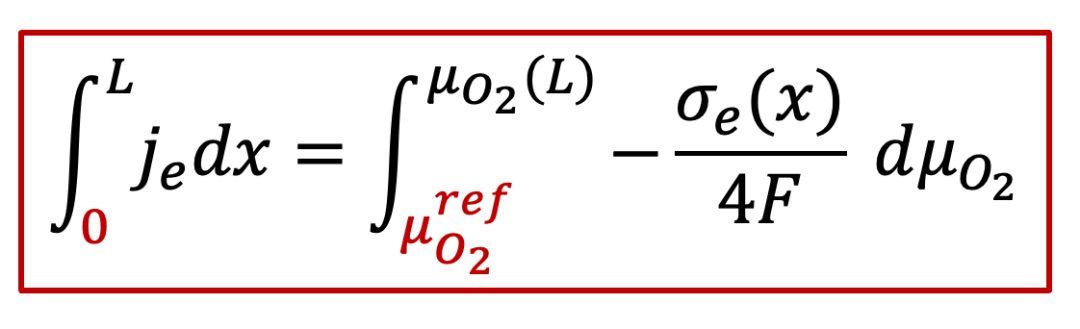




-
离子选择电极2013-03-12 0
-
如何提高负离子发生器的负离子浓度2011-04-12 0
-
基于labview的硅酸根离子浓度检测2016-11-23 0
-
技术讲解—电瓶常见问题之极化22019-12-17 0
-
新的48V锂离子电池Thevein模型里面欧姆内阻,极化内阻,极化电容的数值大概是多少?2020-06-12 0
-
锂离子电池充电的基础知识以及设计注意事项2021-09-14 0
-
学单片机需要什么基础知识2021-10-19 0
-
锂电池配料基础知识2009-10-29 1606
-
天线基础知识(二)2009-11-10 3062
-
锂离子电池知识简介2009-11-13 1381
-
电源管理基础知识电源管理基础知识电源管理基础知识2017-09-15 1532
-
浅谈电瓶修复技术,关于电池极化的知识介绍2020-11-18 3878
-
负离子浓度检测仪的测试原理是哪些2023-06-16 1582
-
天线极化的基础知识2023-12-22 3653
-
Verilog HDL的基础知识2024-10-24 484
全部0条评论

快来发表一下你的评论吧 !

