

如何使用PID控制算法优化控制系统
描述
当涉及到控制系统中的精确调节和稳定性,PID(比例-积分-微分)控制算法是一种不可或缺的工具。本文将简单介绍 PID 控制算法,从基本概念到具体实现,一起了解如何使用 PID 控制算法来优化控制系统。
引言
PID(比例-积分-微分)控制算法作为一种广泛应用的控制策略,在自动化控制系统中扮演着不可或缺的角色。无论是工业生产中的温度控制、机器人运动控制,还是飞行器、医疗设备等领域,PID 控制都发挥着重要作用。
PID 控制算法的核心思想在于基于当前的误差、过去的误差累积和未来的误差变化来调整控制输出,以实现系统的稳定性和响应性能。其中,比例项用于快速响应误差的大小,积分项用于消除稳态误差,而微分项则有助于预测系统未来行为,从而改善系统的稳定性。这三个组成部分相互作用,使得 PID 控制能够在多样化的应用中展现出强大的适应性。
然而,调整 PID 参数并不是一项简单的任务。不同的系统和应用需要不同的参数设置,错误的参数选择可能会导致系统不稳定、震荡或超调。因此,本文将详细介绍不同的调参方法,从手动调节到自动调参算法,为读者提供指导。此外,文章还将通过实际应用案例,深入分析如何根据具体需求来调整 PID 参数,从而实现最佳的控制效果。
除了介绍基本的 PID 控制算法,本文还将涵盖一些改进的 PID 变种,如增强型 PID 和模糊 PID,以应对一些特殊情况下的挑战。这些改进算法在一些复杂的控制系统中能够提供更好的性能和稳定性。
最后,本文还将提供使用 Python 等编程语言实现 PID 控制算法的示例代码,帮助读者更好地理解算法的实际应用。通过结合理论和实践,读者将能够掌握 PID 控制算法的原理和实现方法,为他们在控制系统中的工作提供有力的支持。
基本概念
比例(P)项
比例项反映了当前误差的大小。它使得控制器对误差的变化更为敏感,当误差增大时,控制输出也会增大。比例项的引入能够快速响应误差,但过大的比例系数可能导致系统的震荡和不稳定。
积分(I)项
积分项消除了系统的稳态误差,即长时间内误差无法完全消除的情况。它通过累积过去的误差来调整控制输出,以便逐步消除稳态误差。积分项的引入能够提升系统的稳定性,但过大的积分系数可能导致系统的超调和震荡。
微分(D)项
微分项预测了未来误差的变化趋势,从而帮助系统在误差发生变化之前就采取控制动作。它的引入有助于抑制系统的震荡和超调,但过大的微分系数可能会导致控制器对噪声和干扰过于敏感。
PID 控制算法的组成
PID 控制算法将上述三个项综合考虑,通过加权求和来计算控制输出。其数学表达式为:
其中, 是控制输出, 是当前的误差,、 和 分别是比例、积分和微分系数。
PID 控制算法的调参
调参是 PID 控制算法中关键的一步,合适的参数设置可以使系统达到理想的性能。调参的过程可能需要依赖实验、模拟或自动调参算法。其中,常用的调参方法包括手动调节、Ziegler-Nichols 方法、优化算法等。不同的应用领域和系统类型可能需要不同的参数设置。
PID 控制算法步骤
PID 算法的计算步骤可以总结如下:
- 计算当前误差(偏差),即期望值与实际值之差。
- 根据比例项,计算控制输出变化量,将比例常数与当前误差相乘。
- 根据积分项,计算积分累积值,将积分常数与误差的累积值相乘,并将累积值添加到控制输出。
- 根据微分项,计算误差变化率,将微分常数与误差变化率相乘,并将结果添加到控制输出。
- 将上述三个项的输出相加,得到最终的控制输出。
- 将控制输出应用于系统,控制系统的行为,使其接近期望值。
- 根据系统的响应,不断更新和调整 PID 参数,以达到更好的控制效果。
通过合理地选择和调整比例、积分和微分常数,可以使 PID 算法在不同的控制系统中实现稳定、快速的控制效果。PID 算法的一个挑战是如何根据具体应用场景来确定适当的参数,这通常需要经验和实验来优化。
调参
调参是 PID 控制中至关重要的一步,合适的参数可以使控制系统达到最佳性能。调参通常需要实验和经验,以下是一些常用的调参方法和策略:
- 手动调参: 这是最基本的方法,操作者根据经验和系统特性手动调整 PID 参数。通常从比例项开始,增大 Kp 以观察系统响应。然后根据系统的震荡或过冲情况,逐步调整积分项和微分项。
- 试错法(试-调整法): 这是一种迭代的方法,从初始参数开始,逐步调整参数并观察系统响应。根据系统的性能和稳定性,逐步逼近最佳参数。常见的试错法包括:Ziegler-Nichols 法和 Tyreus-Luyben 法。
- Ziegler-Nichols 方法: 这是一种经典的试错法,首先关闭积分项和微分项,仅调整比例项。从小到大逐步增大 Kp,当系统开始震荡时,记录此时的 Kp 值和震荡周期。然后根据震荡周期计算出 Kp、Ki 和 Kd 的值。
- 专业软件工具: 一些工程领域的专业软件提供自动调参功能,根据系统的数学模型和实时反馈,自动计算出合适的参数。
- 试验分析: 在实际系统中进行多次试验,记录不同参数下的系统响应,并分析数据。根据分析结果来确定最佳参数。
- 频率响应法: 通过对系统进行频率扫描,观察系统的幅频响应和相频响应,从而确定合适的 PID 参数。
- 模拟仿真: 使用数学模型进行模拟仿真,通过模拟观察系统响应,优化参数。
- 自适应控制: 使用自适应控制算法,根据系统的实时状态和响应调整 PID 参数。
- 在线优化: 在实际运行过程中,实时监测系统性能,根据实时数据不断调整 PID 参数,以适应系统变化。
无论使用哪种方法,调参都需要耐心和实验。在调参过程中,要注意以下几点:
- 稳定性: 确保调整后的参数不会引起系统的不稳定性。
- 过冲和震荡: 避免过大的比例增益和微分增益引起系统的过冲和震荡。
- 积分饱和: 积分项可能导致积分饱和问题,导致系统响应变慢或不稳定。
- 系统动态: 考虑系统的动态特性,不同的系统可能需要不同的参数。
调参是一个实践和经验的过程,需要多次尝试和调整,以找到最适合特定应用的 PID 参数。
python 示例
本节提供一个使用 Python 编程语言实现 PID 控制算法的示例代码,并解释如何在实际系统中集成 PID 控制算法。
class PIDController:
def __init__(self, kp, ki, kd):
self.kp = kp
self.ki = ki
self.kd = kd
self.prev_error = 0
self.integral = 0
def update(self, setpoint, current_value):
error = setpoint - current_value
self.integral += error
derivative = error - self.prev_error
output = self.kp * error + self.ki * self.integral + self.kd * derivative
self.prev_error = error
return output
# Example usage
pid = PIDController(kp=1.0, ki=0.1, kd=0.01)
setpoint = 50
current_value = 30
for _ in range(100):
control_output = pid.update(setpoint, current_value)
# Apply control_output to the system
# Update current_value based on system's response
print("Control Output:", control_output)
集成 PID 控制算法:
- 确定系统模型: 在实际系统中集成 PID 控制算法的第一步是了解系统的动态特性,并建立一个合适的数学模型。
- 选择 PID 参数: 根据系统的响应特性和控制要求,选择合适的 PID 参数。可以使用调参方法进行初始参数选择,然后进行现场调整。
- 编写 PID 控制器类: 编写一个 PID 控制器类,其中包含了 PID 参数和控制逻辑的实现。这可以是一个独立的 Python 类或函数。
- 传感器和执行器接口: 将系统的传感器和执行器与 PID 控制器接口对接。传感器提供实际的系统状态信息,执行器接收 PID 控制器的输出并执行动作。
- 实时控制循环: 在主控制循环中,持续获取传感器数据,将其输入 PID 控制器,得到控制输出,然后将输出传递给执行器。这个循环通常以一定的时间间隔运行,以实现实时控制。
- 参数调整和优化: 在实际运行中,监测系统的响应并进行 PID 参数调整。根据系统的实际表现,可以使用手动调整或自动调参算法来优化 PID 参数。
- 系统稳定性和鲁棒性测试: 在集成过程中,进行系统稳定性测试和鲁棒性测试。这涉及到系统对参数变化和外部干扰的响应。
- 迭代和改进: 根据实际测试结果,可能需要进行多次迭代和改进,以确保系统达到所需的性能指标。
在实际应用中,集成 PID 控制算法需要结合领域知识、系统特性和控制要求。通过不断的实验和调整,可以使系统稳定、响应迅速,并达到预期的控制效果。
比如,仿真一个简单倒立摆系统,可以使用如下代码:
import numpy as np
import matplotlib.pyplot as plt
# Constants
g = 9.81 # Acceleration due to gravity (m/s^2)
m = 1.0 # Mass of the pendulum (kg)
l = 1.0 # Length of the pendulum (m)
c = 0.1 # Damping coefficient
# PID parameters
kp = 100.0
ki = 0.0
kd = 0.0
# Initial conditions
theta0 = np.pi / 4 # Initial angle of the pendulum (45 degrees)
theta_dot0 = 0.0 # Initial angular velocity
# Time parameters
dt = 0.01 # Time step
total_time = 10.0 # Total simulation time
# Initialize variables
theta = theta0
theta_dot = theta_dot0
integral = 0
prev_error = 0
# Lists to store data for plotting
time_values = []
angle_values = []
for t in np.arange(0, total_time, dt):
# Calculate error and integral
error = -theta
integral += error * dt
# Calculate derivative
derivative = (error - prev_error) / dt
# Calculate control input using PID formula
control_input = kp * error + ki * integral + kd * derivative
# Update system dynamics using Euler's method
theta_double_dot = -g / l * np.sin(theta) - c / (m * l**2) * theta_dot + control_input
theta_dot += theta_double_dot * dt
theta += theta_dot * dt
# Store data for plotting
time_values.append(t)
angle_values.append(theta)
# Update previous error for derivative term
prev_error = error
# Plot results
plt.plot(time_values, angle_values)
plt.xlabel('Time (s)')
plt.ylabel('Angle (radians)')
plt.title('Inverted Pendulum Control using PID')
plt.grid(True)
plt.show()
结果如下:
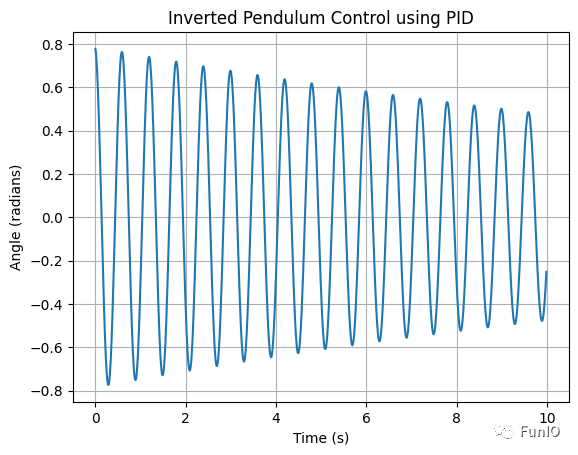
kp = 100.0, ki = 0.0, kd = 0.0
试了几次,保持 kp 不变,ki = 0.1, kd = 50.0,结果如下:
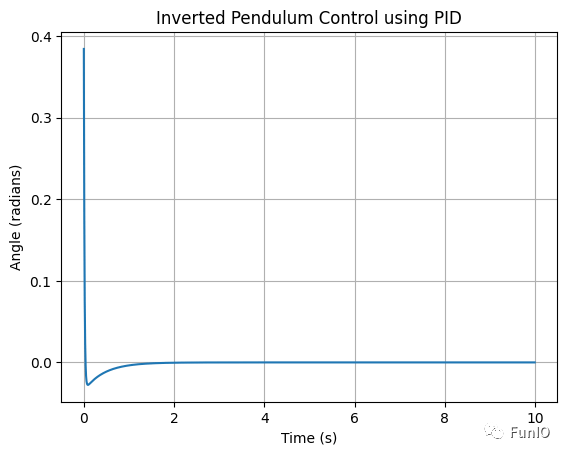
kp = 100.0, ki = 0.1, kd = 50.0
这个波形是不是有些眼熟?没错,跟 dcdc 稳压输出的波形很像!
局限和改进
局限性:
- 线性假设: PID 控制是基于线性模型的假设,对于非线性系统可能不适用或需要更复杂的控制方法。
- 固定参数: 传统 PID 控制的参数是固定的,难以应对系统参数变化或外部干扰。
- 复杂系统: 在复杂的多变量系统中,单一的 PID 控制往往难以满足需求。
- 不稳定性: 不正确的参数调整可能导致系统的不稳定,甚至失控。
- 不适合开环系统: 对于开环系统(无反馈)或系统稳定性差的情况,PID 控制效果有限。
改进方法:
- 自适应 PID: 自适应 PID 控制根据系统实际响应动态调整 PID 参数,适应系统变化。
- 增加前馈控制: 前馈控制能够在系统发生变化前预先调整控制输出,提高系统的响应速度和稳定性。
- 模糊 PID: 将模糊逻辑与 PID 结合,使控制更适应复杂和非线性系统。
- 神经网络 PID: 使用神经网络模型来优化 PID 参数,适应更广泛的系统。
- 非线性 PID: 使用非线性 PID 方法,如广义 PID,能够更好地应对非线性系统。
- 鲁棒 PID: 鲁棒 PID 控制考虑到参数不确定性和外部扰动,增强系统的稳定性和鲁棒性。
- 模型预测控制: 使用系统的数学模型进行预测,优化控制输出,适用于复杂动态系统。
- 优化算法: 使用优化算法,如遗传算法、粒子群算法等,自动寻找最佳 PID 参数。
- 混合控制: 将多个控制方法结合,形成混合控制策略,以应对复杂系统。
- 现代控制理论: 使用现代控制理论,如状态反馈、输出反馈等,适应多变量和复杂系统。
尽管传统 PID 控制在许多应用中仍然有效,但针对局限性和需求,不断发展的改进方法能够使控制系统更加稳定、快速和适应不同情况。
-
PID电机控制系统(控制原理+控制算法+程序范例)2019-03-18 0
-
模糊PID控制算法如何控制匀速升温2019-05-30 0
-
连续控制系统的PID算法及MATLAB仿真2021-08-11 0
-
智能PID算法在液位控制系统中的应用2009-09-01 481
-
基于Fuzzy PID的陀螺仪温度控制系统设计2009-12-04 710
-
常用的PID控制系统技术及仿真2010-04-28 545
-
基于数字PID控制算法的温度控制系统2011-01-05 903
-
位置式PID控制算法研究2011-03-16 1207
-
基于Matlab的网络控制系统模糊控制算法应用研究2013-09-25 732
-
PID控制算法控制算法2016-11-17 908
-
基于模糊PID算法的船舶锚机控制系统设计_李元贵2017-01-18 684
-
基于增量式PID算法的帆板控制系统的设计张存吉2017-03-15 1044
-
基于改进遗传算法的气体混合控制系统的设计与仿真2018-03-01 862
-
如何使用免疫粒子群优化算法实现增量式的PID控制2019-11-01 1092
-
PID算法在控制系统中的特性和指标2023-08-22 1621
全部0条评论

快来发表一下你的评论吧 !

