

信号完整性-电流分布及集肤深度介绍
电子说
描述
10.1 电流分布及集肤深度
在估算导线的电阻和电感时,假设电流在导线中是均匀分布的。直流时的情况的确如此,但电流变化时的情况就不总是这样了。交流时的电流分布大不相同,将会明显地影响导线的电阻,并对导线的电感产生一定的影响。
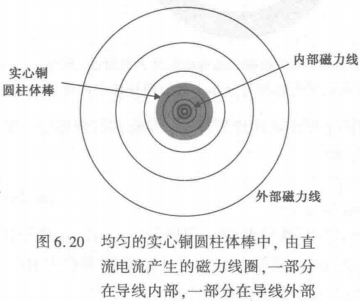
直流时,实心铜棒中的电流是均匀分布的。前面在计算磁力线匝数时,重点关注了导线外部的磁力线。事实上,在导线内部也有一些磁力线,它们是自感的一部分,如上图所示。
导线内部和导线外部的磁力线圈都能影响自感。为了区分它们,我们把自感分为内部自感和外部自感。
内部磁力线圈是穿过导线金属并受金属影响的那部分。圆导线的外部磁力线圈并不穿过导线,也不会随频率而变化。但是,由于导线内部的电流分布随频率而变化,所以导线内部的磁力线圈也将发生变化。
导线中流过单位安培电流时,与电流分布在外表面相比,电流集中在圆柱杆中心时有更多的磁力线和更大的自感。
此时的电流是正弦波,任何频率分量都是沿最低的阻抗路径传播的。电感最大的电流路径,其阻抗也最大;随着频率的升高,高电感路径的阻抗会变得更大。频率越高,电流越倾向于选择电感较低的路径,即趋向于圆柱杆外表面的路径。
一般而言,频率越高,电流越趋向于沿着导线的外表面流动。在某一给定频率,从导线内部到外部表面有特定的电流分布。这取决于电阻性阻抗与感性阻抗的相对大小。电流密度越集中,电阻性阻抗上的压降就越大。但是频率越高,内部路径和外部路径感性阻抗的差别就越大。这样的权衡意味着电流分布随频率而变化,并且在高频时,所有电流会趋向于导线表面的那一薄层。
对于实际导线中的电流分布,只有为数不多的一些几何结构有很好的近似,圆柱体是其中之一。对于每个频率点,从导线表面到导线中心,电流分布呈指数下降,在这种几何结构中,可以把电流层近似成有固定厚度δ的均匀分布,并称该等效厚度为 集肤深度 ,它取决于频率、金属的电导率和磁导率,即:

其中,δ表示集肤深度,σ表示金属的电导率,μ_0表示自由空间的磁导率,μ_r表示导线的相对磁导率,f表示正弦波频率。
铜的电导率为5.6×10^7S/m,相对磁导率为1,它的集肤深度近似为

在1MHz时,铜的集肤深度为66μm。对于1盎司铜线,当电流正弦波频率高于10MHz时,电流分布取决于集肤深度而不是横截面的结构。当低于10MHz时,电流是均匀分布的,且与频率无关。当集肤深度小于横截面几何厚度时,电流分布、电阻和回路电感开始与频率有关。
经验法则 :当威廉希尔官方网站 板上的铜线为1盎司或者几何厚度为35μm时,若频率大于等于10MHz,则导线中的电流不再占用线条的整个横截面,趋肤效应在电流分布中起主导作用。
在实际的互连中,通常有信号路径和返回路径。由于电流回路沿信号路径和返回路径传播,回路自感影响着电流所感受到的阻抗。随着频率升高,回路自感的阻抗变大,导线中的电流将选择阻抗最小即回路自感最小的路径而重新分布。回路自感最小时电流是如何分布的?
以下两种效应都会出现:电流在导线内会向外扩散开,两条导线中的电流重新分布以使两个电流相互靠得更近。两种力量的平衡决定了每条导线中的电流的确切分布。每条导线中的电流都会尽量向周边扩散开,以减小局部自感。与此同时,两条导线中的电流又会尽可能地挤近,以增大局部互感。
集肤深度小于横截面的几何厚度时,随着频率的升高,电流流过的横截面积随频率的平方根成比例减小,从而使导线的单位长度电阻随频率的平方根成比例增大。
以简单的微带线为例,假设微带线由1盎司铜构成,宽为5mil。在直流时,信号路径的单位长度电阻为R_DC=ρ/ωt,R_DC表示直流时的单位长度电阻,ρ表示铜的体电阻率,ω表示信号线的宽度,t表示信号线的几何厚度。
在频率约高于10MHz时,电流受集肤深度的限制,电阻与频率有关。此时电流实际所用的导线厚度约等于集肤深度,所以高频时的电阻实际上就是R_HF=ρ/ωδ,R_HF表示高频时的单位长度电阻,δ表示高频时铜的集肤深度。当频率更高时,电阻大致随频率的平方根而增大。
电流随着频率的升高而重新分布,直接造成电阻随频率而升高。由于促使电流重新分布的动力是追求回路电感的减小,所以回路自感必将随频率的升高而减小。
直流时,导线的自感由外部自感和内部自感两部分组成。当导线中的电流重新分布时,外部自感不变;随着越来越多的电流向导线表面移动,内部自感越来越小。当电流频率远高于集肤深度约等于导线几何厚薄的这个频率时,导线内部的电流会非常小,而内部自感此时几乎为零。
可以推测导线的自感与频率有关。低频时的导线自感等于L_internal+L_external,高频时的导线自感等于L_external。这种转变应当从集肤深度与导线几何厚薄相当时的这个频率开始显现,并且从集肤深度只占几何厚薄很小一部分时的这个频率起,基本趋于稳定。
微带线回路自感,通常是指所有电流都跑到外表面的高频界限的情况。如果电流靠近导线表面而且与导线几何厚薄无关,这一频率就是趋肤效应的界限,“高频”是指高于这一界限的频率。
10.2 高磁导率材料
导体的磁导率是影响集肤深度的重要参数,磁导率高的金属只有少数几种。磁导率是指导体与磁力线圈之间的相互作用,大多数金属的磁导率为1,所以它们对磁力线圈没有影响。
当磁导率大于1时,金属内的磁力线匝数比磁导率为1时更多。只有3种金属的磁导率大于1,它们是铁磁体金属:铁、钴和镍。大多数含有这些金属合金的磁导率都远大于1。我们最熟悉的铁氧体中常含有铁和钴,其磁导率大于1000。合金42和科瓦合金(Kovar)这两种铁磁体是重要的互连金属,其磁导率为100~500。用这些高磁导率金属制成的互连,它们的电阻及电感值与频率有很大的关系。
对于铁磁体导线而言,直流时它的自感包括内部自感和外部自感两部分。外部自感所对应的磁力线圈穿过的是磁导率为1的空气,所以铁磁体导线的外部自感保持不变,与铜导线时的情况一样。总之,单位安培电流时的外部磁力线是相同的。
但是,铁磁体导线的内部磁力线穿过的是高磁导率材料,这时磁力线会激增。低频时,铁磁体导线的电感非常大,但当频率约高于1MHz时,所有磁力线中只剩下外部磁力线,其回路自感和相同尺寸的铜导线的回路自感相当。
超过集肤深度极限时,回路电感几乎仅由外部磁力线构成,所以铁磁体导线中的高频信号感受到的回路电感与铜导线的回路电感大致相当。
在相同频率下,镍导线中的电流横截面要比相同几何结构的铜导线的薄得多,集肤深度约为铜的1/5。另外,体电阻率也比较高,这导致串联电阻更大。镍导线的电阻是同频率下铜导线电阻的10倍;很明显,镍导线的电阻随着频率的平方根而增大,这正是趋肤效应限制下电流分布的特点。与一般非铁磁体的引线相比,合金42和科瓦合金引线的高频电阻就显得很高。
这就是有时在合金42引线上镀银以减小其高频电阻的原因。在外表面使用非铁磁体导线,以便传输高频电流。让最高的频率分量途经集肤深度更大和电导率更高的材料。
10.3 涡流
如果两个导体中有一个导体的电流改变,那么另一个导体的两端会产生感应电压,此感应电压会形成电流。换言之,当其中一个导体的电流变化时,第二个导体中会产生感应电流,我们称这种电流为 涡流 ( 镜像电流 )。
举一个最简单的例子,金属平面上方有条圆导线,该金属平面可以是任何导体并可能悬浮有任何电压。至于电压是多大或平面又与什么相连,都不重要,重要的是它能够导电而且是连续的。
当导线中有电流时,一些磁力线就会穿过导电平面,导线与平面之间就会存在互感。当导线中的电流变化时,穿过平面的磁力线也会发生变化,并在平面上产生感应电压,而此电压又激起了涡流,这些涡流反过来又会产生自己的磁力线。
涡流与实际电流大小相等,方向相反,而且涡流的一些磁力线会环绕在实际电流周围。不过,由于两电流方向相反,在实际电流的磁力线中要减去涡流的磁力线。
源于涡流的互磁力线圈将减小导线的总电感,实际上就是减小了导线的局部自感。如果电流回路在悬空的导电平面上方,而且二者绝对没有任何的电气连接,仅仅是平面的存在就已减小了回路的回路电感。
导线离平面越近,离涡流就会越近,它们之间的互感也就越大,从而实际电流的局部自感就越小。下面的悬空平面越近,平面中产生的涡流就越大,信号路径的自感也就越小。
-
信号完整性是什么2021-01-25 0
-
信号完整性与电源完整性的相关资料分享2021-11-15 0
-
详解信号完整性与电源完整性2021-11-15 0
-
何为信号完整性?信号完整性包含哪些2021-12-30 0
-
信号完整性原理分析2009-11-04 1055
-
什么是信号完整性2009-06-30 5332
-
信号完整性与电源完整性仿真分析2011-11-30 1834
-
信号完整性分析2011-11-30 7577
-
信号完整性原理2016-08-29 992
-
PCB信号完整性有哪几步_如何确保PCB设计信号完整性2018-05-23 11274
-
信号完整性系列之信号完整性简介2021-01-20 1515
-
信号完整性系列之“信号完整性简介”2021-01-23 2002
-
信号完整性与电源完整性的仿真2021-09-29 1327
-
PCB电流与信号完整性设计.zip2022-12-30 690
-
听懂什么是信号完整性2024-12-15 229
全部0条评论

快来发表一下你的评论吧 !

