

浅析机器学习的基本步骤
人工智能
描述
机器学习的基本步骤及实现方式比较
机器学习(Machine Learning)是计算机科学与人工智能的重要分支领域,也是大数据时代的一个重要技术。机器学习的基本思路是模仿人类的学习行为过程,该技术主要采用的算法包括聚类、分类、决策树、贝叶斯、神经网络、深度学习等。总体而言,机器学习是让计算机在大量数据中寻找数据规律,并根据数据规律对未知或主要数据趋势进行最终预测。在机器学习中,机器学习的效率在很大程度上取决于它所提供的数据集,数据集的大小和丰富程度也决定了最终预测的结果质量。目前在算力方面,量子计算能超越传统二进制的编码系统,利用量子的纠缠与叠加特性拓展其对大量数据的运算处理能力,从而能得出更准确的模型参数以解决一些或工业或网络的现实问题。
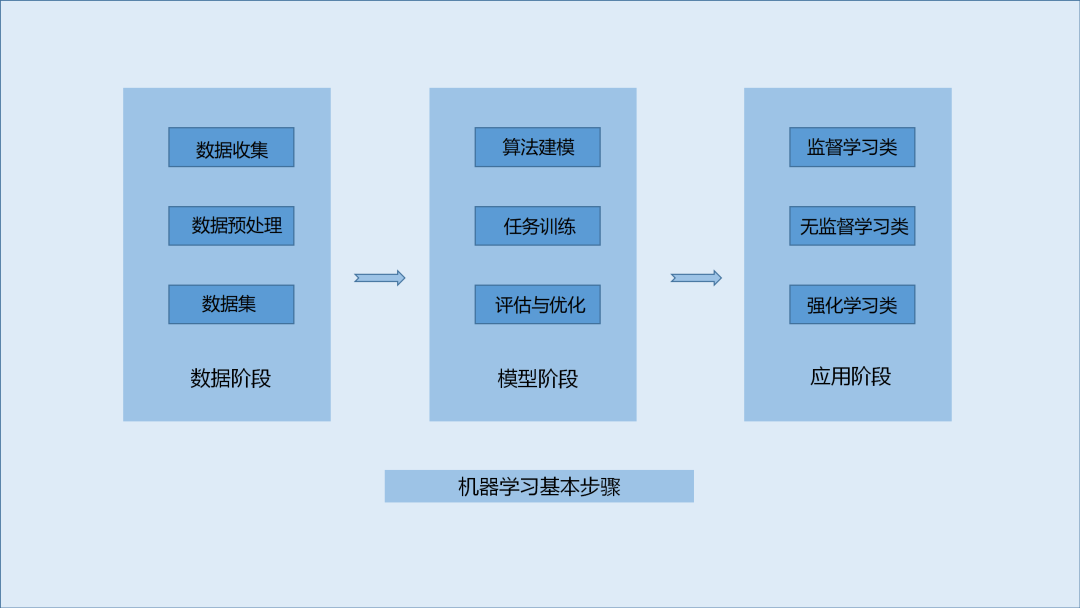
1.数据阶段
1.1数据收集与预处理
互联网时代,每分每秒中都有大量的数据信息产生。大量的数据如同养料一般,没有源源不断地数据供应,以数据为基础发展起来的各种技术如同无源之水缺少发展的活力。数据采集技术已经有了阶段性的发展,成熟度相对较高。因此,在提及机器学习、深度学习、自然语言处理等人工智能技术时,数据采集常常被忽略。
数据采集技术也造就了许多以采集数据为主要业务的产品与应用,如作为Hadoop的组件的Flume、开源的数据收集架构Fluentd、Python的爬虫架构Scrapy等。还有一些数据收集服务平台如百度统计、阿里云、大数据采集工具八爪鱼。
尽管数据时代不缺少数据,但有价值信息的数据即有效数据还需要对大量无序的数据进行数据预处理。未经过数据处理的数据往往存在以下问题:
数据不完整:缺少属性值或仅仅包含聚集数据;
数据含噪声:大量数据中包含错误或偏离期望的离群值;
数据标签规则不一:对于数据的分类规则与标准不一致,导致最终收集的数据不属于同类数据。
数据预处理的方法主要有以下几种:
数据清洗:对数据进行清洗,以去除噪声、无关数据、完整性及其欠缺的数据、补充轻微缺损的数据;
数据集成:数据集成多为数据分析的一个环节,数据集成将多个数据源中的数据结合、存放在一个一致的数据存储,如数据仓库中,这些数据源可能包括多个数据库、数据方或一般文件;
数据规约:数据归约技术可以用来得到数据集的归约表示,可以尽可能保持原数据的完整性,因而在归约后的数据集上挖掘将更有效,并产生几乎相同的分析结果。
1.2数据集准备
数据集准备是使用TensorFlow、Paddle Quantum等进行机器学习的入门基础。在实际练习或使用过程中,企业的数据相对而言获取渠道固定、有较清晰的分类,因此在准备数据集时,做好分类后只需要将数据文件转为机器学习可识别的文件即可。个人练习过程中,数据获取难度较大,可参考KDnuggets上发表的一篇文章,作者总结了七十多个免费的数据集(http://t.cn/RQJhwSi)。
经处理后的数据制备为数据集。数据集一般可以分为训练集、验证集、测试集。其中,训练集主要用于训练模型;验证集主要用于选择模型,通常在训练过程中使用训练集确定一些超参数;测试集主要用于判断网络性能的好坏。
数据集的划分方法一般也为三种,即留出法、交叉验证法、自助法。留出法是指将数据集 D 划分成两份互斥的数据集,一份作为训练集 S,一份作为测试集 T,在 S 上训练模型,在 T 上评估模型效果。留出法的优点是简单好实现,但训练集和测试集数据分布不一致时易引入偏差,最终影响数据模型评估结果。交叉验证法是将数据集D划分为n个互斥的子集。然后每次选用一份数据子集作为测试集,其余的 n-1 份数据子集作为训练集,迭代n轮得到n个模型,最后将n次的评估结果汇总求平均值得到最终的评估结果。自助法使用有放回的重复采样方式进行训练集、测试集的构建。自助采样即确定所获取的训练集样本数n后,从数据集D中有放回的采样n次,得到n条样本的训练集,最后将未出现过的样本作为测试集。
2.模型阶段
2.1机器学习算法建模
机器学习可为监督学习、无监督学习和强化学习三类。监督学习是指有标签数据、可进行直接反阔并预测结果的一种学习方式,其主要目标是从有标签的训练数据中学习模型,从而对未知的数据做出预测。无监督学习是指数据没有标签且数据结构不明确或无数据结构的。无监督学习技术主要目的是在没有已知结果变量或奖励函数的指导下,探索数据结构、提取有价值的信息。强化学习的主要目的是开发一个系统,然后通用该系统与环境之间发生交互产生的数据信息提高系统性能。强化学习(RL)分反馈是通过奖励函数对行动度量的结果,常见的强化学习场景如国际象棋、制造机器人、管理生产规划、企业决策、物流、威廉希尔官方网站 设计、控制自动驾驶汽车、控制无人机等等。
2.2模型训练
模型训练需要进行多轮迭代,每轮迭代需要遍历一次训练数据集并从中获取小批量样本。获取样本后将样本数据输入模型中得到预测值,对比预测值与真实值之间的损失函数(loss)。在得到损失函数以后,开始执行梯度反向传播并根据设置的优化算法更新模型参数。最后模型的训练效果可通过损失函数值的变化来判断,当损失函数呈减小趋势,模型训练效果越显著。以spam数据集为例:
将数据分为训练集和测试集并拟合模型
##codes from https://cloud.tencent.com/developer/article/1787782
library(caret)
library(kernlab)
data(spam)
inTrain <- createDataPartition(y = spam$type,
p = 0.75, list = FALSE)
training <- spam[inTrain, ]
testing <- spam[-inTrain, ]
modelFit <- train(type ~., data = training, method="glm")
查看选项:metric选项设置算法评价,连续变量结果为均方根误差RMSE;R^2^(从回归模型获得)分类变量结果为准确性;Kappa系数(用于一致性检验,也可以用于衡量分类精度)
##codes from https://cloud.tencent.com/developer/article/1787782
args(train.default)
function(x, y, method = "rf", preProcess = NULL, ..., weights = NULL,
metric = ifelse(is.factor(y), "Accuracy", "RMSE"), maximize = ifelse(metric == "RMSE", FALSE, TRUE),
trControl = trainControl(), tuneGrid = NULL, tuneLength = 3)
NULL
args(trainControl)
function (method = "boot", number = ifelse(grepl("cv", method),
10, 25), repeats = ifelse(grepl("[d_]cv$", method), 1, NA),
p = 0.75, search = "grid", initialWindow = NULL, horizon = 1,
fixedWindow = TRUE, skip = 0, verboseIter = FALSE, returnData = TRUE,
returnResamp = "final", savePredictions = FALSE, classProbs = FALSE,
summaryFunction = defaultSummary, selectionFunction = "best",
preProcOptions = list(thresh = 0.95, ICAcomp = 3, k = 5,
freqCut = 95/5, uniqueCut = 10, cutoff = 0.9), sampling = NULL,
index = NULL, indexOut = NULL, indexFinal = NULL, timingSamps = 0,
predictionBounds = rep(FALSE, 2), seeds = NA, adaptive = list(min = 5,
alpha = 0.05, method = "gls", complete = TRUE), trim = FALSE,
allowParallel = TRUE)
NULL
trainControl控制训练方法:设置重抽样方法,boot:bootstrapping自举法,boot632:调整的自举法,cv:交叉验证 repeatedcv:重复交叉验证,LOOCV:留一交叉验证;number选项设置交叉验证或自举重抽样的次数;repeats选项设置重复交叉验证的重复次数;seed选项设置随机数种子,可以设置全局随机数种子,也可为每次重抽样设置随机数种子。
##codes from https://cloud.tencent.com/developer/article/1787782 set.seed(1235) modekFit2 <- train(type ~., data = training, method = "glm") modekFit2 Generalized Linear Model 3451 samples 57 predictor 2 classes: 'nonspam', 'spam' No pre-processing Resampling: Bootstrapped (25 reps) Summary of sample sizes: 3451, 3451, 3451, 3451, 3451, 3451, ... Resampling results: Accuracy Kappa 0.9156324 0.8229977
2.3模型评估与优化
在机器学习的算法模型中,参数包括两类分别为模型参数和超参数。其中模型参数不能人为预先设置,而是通过模型训练过程中自动生成与更新。另一类参数为超参数。超参数在模型训练之前就可认为设定,是控制模型结构、功能、效率的一个调节入口。模型训练过程中产生的损失函数是进行模型评估的一个指标,在模型训练过程结束后,可根据得到的各指标值对模型进行评估与优化。模型优化中涉及到一个超参数概念,是指在建模时将一些与模型无关的未知量设置为固定参数。常见超参数有学习效率、迭代次数(epoches)、隐层数目、隐层单元数、激活函数、优化器等。
2.4预测或推理
机器学习的预测即在模型中输入一个预测值,通过模型计算可以得到对应的输出值,该值即为模型的预测结果。简单的模型如一般简单线性回归y=kx+b。真实值分布在线性模型两侧,输入一个对应的x值即得到一个对应的y值。
3.SVM算法示例
SVM是一类有监督的分类算法,该算法思想主要为:首先假设样本空间上有两类样本点,SVM算法核心是希望找到一个超平面将两类样本分开;在寻找划分超平面时应尽可能使得两类样本到超平面距离最短。
首先,导入依赖,准备算法运行环境
import qiskit import matplotlib.pyplot as plt import numpy as np from qiskit.ml.datasets import ad_hoc_data from qiskit import BasicAer from qiskit.aqua import QuantumInstance from qiskit.circuit.library import ZZFeatureMap from qiskit.aqua.algorithms import QSVM from qiskit.aqua.utils import split_dataset_to_data_and_labels, map_label_to_class_name
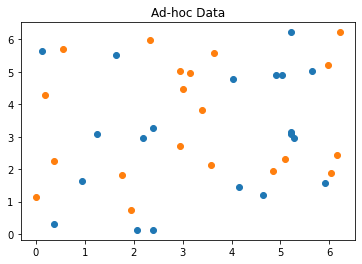
其次,加载并查看数据
feature_dim = 2
training_dataset_size = 20
testing_dataset_size = 10
random_seed = 10598
shot = 10000
sample_Total, training_input, test_input, class_labels = ad_hoc_data(training_size=training_dataset_size,
test_size=testing_dataset_size,
gap=0.3,
n=feature_dim,
plot_data=True)
datapoints, class_to_label = split_dataset_to_data_and_labels(test_input)
print(class_to_label)
方式一:采用量子后端的方式运行SVM算法
使用'qasm_simulator'作为算法后端
#getting my backend
backend = BasicAer.get_backend('qasm_simulator')
feature_map = ZZFeatureMap(feature_dim, reps=2)
svm = QSVM(feature_map,training_input,test_input,None)
svm.random_seed = random_seed
quantum_instance = QuantumInstance(backend,shots=shot,seed_simulator=random_seed, seed_transpiler=random_seed)
result = svm.run(quantum_instance)
打印训练中的核心矩阵
print("kernel matrix during the training:")
kernel_matrix = result['kernel_matrix_training']
img = plt.imshow(np.asmatrix(kernel_matrix),interpolation='nearest',origin='upper',cmap='bone_r')

获得预测及其精度
predicted_labels = svm.predict(datapoints[0])
predicted_classes = map_label_to_class_name(predicted_labels,svm.label_to_class)
print('ground truth: {}'.format(datapoints[1]))
print('prediction: {}'.format(predicted_labels))
print('testing success ratio: ', result['testing_accuracy'])
输出预测结果
ground truth: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] prediction: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] testing success ratio: 1.0
由以上输出可看出,采用量子方式运算SVM算法的精度结果为100%。
方式二:采用经典方式运行SVM算法
使用qiskit中的一个类似Scikit-learn实现
from qiskit.aqua.algorithms import SklearnSVM svm_classical = SklearnSVM(training_input, test_input) result_classical = svm_classical.run()
打印经典方式训练中的kernel matrix
print("kernel matrix during the training:")
kernel_matrix_classical = result['kernel_matrix_training']
img = plt.imshow(np.asmatrix(kernel_matrix_classical),interpolation='nearest',origin='upper',cmap='bone_r')

打印预测结果及精度
predicted_labels_classical = svm_classical.predict(datapoints[0])
predicted_classes_classical = map_label_to_class_name(predicted_labels,svm.label_to_class)
print('ground truth: {}'.format(datapoints[1]))
print('prediction: {}'.format(predicted_labels_classical))
print('testing success ratio: ', result_classical['testing_accuracy'])
采用经典方式的SVM算法输出结果如下:
ground truth: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1] prediction: [1. 0. 0. 1. 0. 0. 0. 0. 1. 0. 1. 1. 1. 0. 0. 0. 0. 1. 1. 1.] testing success ratio: 0.65
由以上输出可看出,采用经典方式运算SVM算法的精度结果为65%。
在SVM算法的分类中,寻找可划分两类样本的超平面通常只能在更高维度上进行,这就涉及到计算高维空间中的样本点与平面之间的距离。因此,当维度非常大时,样本点与超划分平面的距离计算耗费将很大。而内核计算可以获取数据点后返回一个距离,并可以通过优化内核使样本点到超平面的距离最大化。这时,量子计算的高效率的计算模式就体现出其优越性,该示例在一定程度上说明了QSVM优于SVM。
编辑:黄飞
-
机器人操作系统浅析2016-09-28 0
-
介绍机器学习的基础内容2021-08-13 0
-
机器学习的基础内容2021-08-20 0
-
浅析嵌入式学习步骤2021-11-05 0
-
机器学习的基础内容大合集2022-01-07 0
-
机器学习的基础内容介绍2022-01-12 0
-
机器学习的基础内容汇总2022-02-28 0
-
什么是机器学习? 机器学习基础入门2022-06-21 0
-
从零到python机器学习大神的7个步骤2017-11-15 13078
-
如果要从事机器学习方面的研发,可以按照以下几个步骤学习2019-09-20 3281
-
机器学习模型切实可行的优化步骤2020-05-04 2761
-
浅析嵌入式Linux学习的八大步骤2021-01-01 1028
-
机器学习算法汇总 机器学习算法分类 机器学习算法模型2023-08-17 1258
全部0条评论

快来发表一下你的评论吧 !

