阻抗控制在频域范围内的定义

阻抗控制在频域范围内的定义：

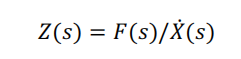
考虑到交互力与位置的关系，可以演变为如下模式：

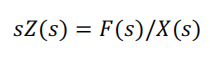
阻抗可以以期望惯量、阻尼与刚度的形式呈现，因此：

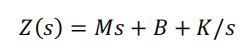
可实现程序如下：

Z=Md*s+Bd+Kd*(1/s);
bode(Z)
grid on

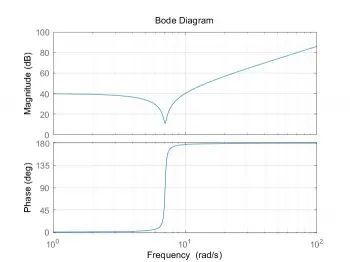
仿真结果如下：

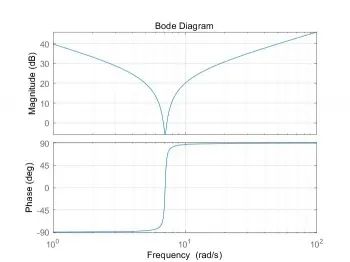
从分析结果中可以看出，虚拟动态模型存在一个凹形状，这是由于系统动态的影响因素。

当考虑到交互力与位置的频域幅频特性关系时，可以用以下代码进行分析：

Z=Md*s+Bd+Kd*(1/s);
bode(Z)
bode(s*Z)
grid on

而阻抗控制在时域上的微分方程形式如下：

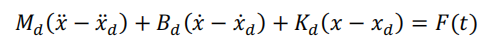
理解： 硬件和控制器之间的物理等价性。这意味着不仅受控系统的硬件组件可以影响物理系统的表面行为，而且控制器也可以影响。换句话说，控制器对受控物理系统的最终效果不仅仅是控制运动或力，而是 修改其表观动态特性 。

检测到外力并产生相应的执行器力来辅助机器人的运动，这使受控系统执行一个修正的行为。

阻抗的势与流： 势（即力）输入和流量（即运动）输出，阻抗代表了从运动到力的因果关系。

阻抗控制与其他控制方法相比较，明显的优势： 位置控制适用于自由运动，而不是受约束的运动。力控制需要接触力的反馈信息。因此，它不能在自由空间中工作。

混合位置/力控制将任务空间划分为两个子空间，称为位置控制和力控制子空间。在操作过程中，必须根据相应的子空间来切换控制规律，这可能会导致响应的不稳定。相比之下，阻抗控制是一种统一的控制策略，适用于所有的操作阶段，包括自由运动、约束运动和瞬态阶段，而不需要切换控制模式。

阻抗控制在笛卡尔空间中的动态模型：

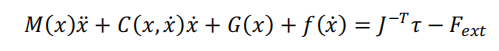
期望的动态行为表达：

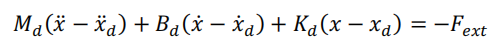
联立两个公式就可以得到机器人控制律：

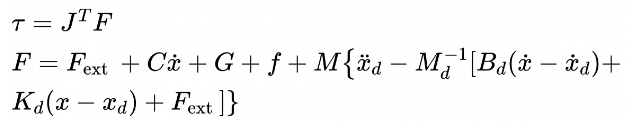
用期望的阻抗来“掩盖”原始行为，即通过利用硬件的固有特性，可以在没有反馈的情况下调节末端的阻抗行为。

为了凸显阻抗控制方法，简化了机器人系统，Simulink可实现模型：

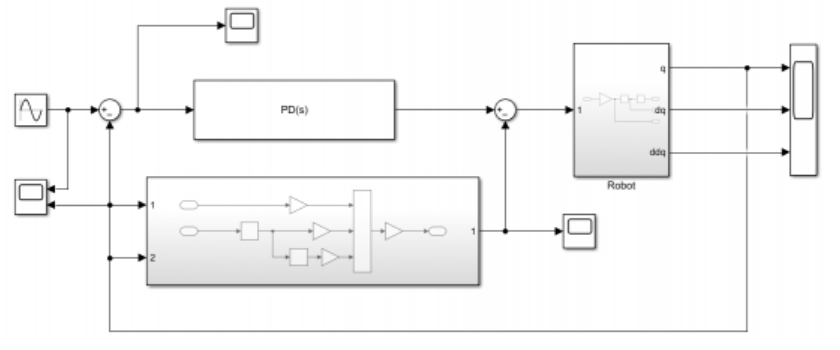
基于上述模型，采用单关节机器人来验证阻抗控制算法的有效性。

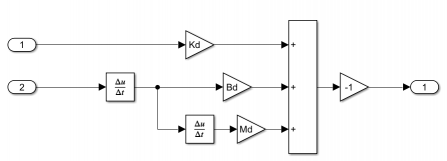
机器人实际位置，速度与加速度仿真分析结果如下：

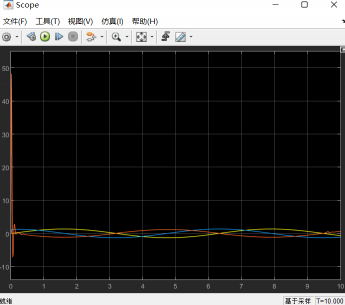
轨迹跟踪误差结果如下：

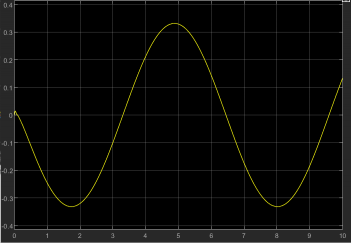
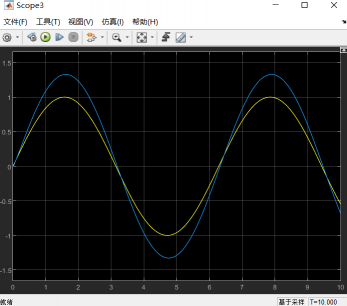
期望运动与实际运动：（由于阻抗呈现的刚柔因素，需要进行控制参数的调节可实现期望的动态平衡）

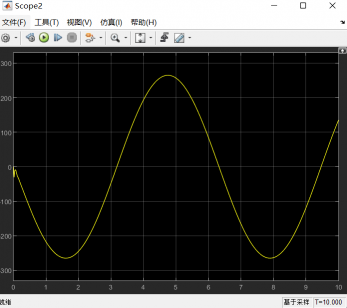
阻抗控制输出的力修正量：

存在的问题

稳定性问题、力跟踪方法、混合阻抗控制、鲁棒性方法、自适应算法、学习控制等。模型的不确定性和未知的环境是阻抗控制中不可避免的困难。

为了减少这些问题的负面影响，将一些先进的控制技术与阻抗控制相结合，包括鲁棒方法、自适应方法和学习方法。自适应阻抗控制方法可进一步分为两类。

其中一类是处理模型的不确定性。另一个目的是增强对未知环境的适应性。处理未知环境的方法通常被称为可变阻抗控制，因为阻抗模型的参数值是可变的，以适应变化的环境。应用神经网络技术，提高了控制器对模型不确定性的鲁棒性。

关键： 使机器人操作能够更好地实现不确定动态和不确定环境下的动态交互。