光束整形中的自由曲面衍射光学设计

从远古时代，人类就一直在努力改造和整束光线——从阿基米德来烧毁罗马船只的镜面盾，到菲涅尔大的手工打磨的灯塔透镜，再到今天的微光学元件，我们希望光能准确地到达我们想要它到达的地方。

光束整形是一种重要的光学技术，它通过改变入射激光光束的相位分布或者振幅分布，使出射光束在目标面上具有特定的辐照度（或光强）分布。换句话说，光束整形技术能够实现激光光束能量分布的良好控制，目前已经被广泛应用于材料加工、医疗、激光打印、光学数据存储、光谱学等方面。

光束整形方法主要分为几何光学方法和物理光学方法两大类。其中，几何光学方法由于忽略了衍射效应，导致一些情形下的光束整形效果不够精细，但却能为物理光学方法提供良好的优化起点。因此，结合几何光学方法和物理光学方法的复合设计方法，能够设计出易于加工的自由曲面衍射光学元件，同时能抑制杂散光和散斑噪声。

非薄元近似和非傍轴情形下，基于几何光学构建光学自由曲面是一个更为复杂的反问题，文中不涉及。下面我们来看看，在考虑衍射效应的基础上，光束整形DOE的物理光学设计方法以及结合几何光学方法与物理光学方法的复合设计方法。  

传统物理光学设计方法

基于波动光学理论描述光场传播的物理光学方法，是一种精确的光束整形方法。该方法通过纯相位型衍射光学元件（DOE）改变入射光场的相位分布，从而在目标面上产生特定的辐照度分布。相比于传统的折反射光学器件，DOE的质量更轻，体积更小，能实现传统折反射光学器件难以实现的集成化、阵列化等功能，更符合光电系统轻量化、微型化的发展趋势。例如一些智能手机采用DOE在有限空间内生成特定的点阵用于人脸识别。

薄元近似下，DOE的面型高度与其对应的相位分布成线性关系。此时DOE的设计问题等价为根据入射面和目标面辐照度分布恢复中间调制元件的相位分布问题。目前，相位恢复问题的物理光学求解方法主要包括：迭代傅里叶变换算法（IFTA）和最优化方法。

1972年，Gerchberg和Saxton提出了经典的GS算法，开创了IFTA的先河。GS算法预先设定一个相位初值，通过快速傅里叶变换（FFT）和逆傅里叶变换（IFFT）在空域约束集和频域约束集来回迭代从而恢复出未知的相位信息，原理如图1所示。

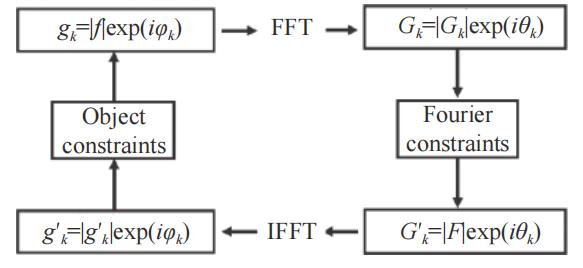
图1 GS算法原理图

将GS算法中的傅里叶变换过程改为不同的衍射传播过程能够实现不同场景下的相位恢复，如迭代角谱算法就是将傅里叶变换过程替换为角谱传播过程，从而能够适用于更广泛的衍射场景。GS算法在第k次迭代的过程概括如下：

（1）对输入面光场gk (x,y)进行傅里叶变换得到频域面光场Gk (u, v)；

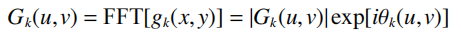
式中：(x,y)和(u, v)分别为输入面和频谱面点的坐标。

  （2）将计算得到的频域面光场振幅|Gk(u, v)|替换为已知的光场振幅|F(u, v)|；

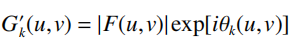
（3）对G'k(u, v)作逆傅里叶变换得到传播回来的输入面光场g'k(x,y)；

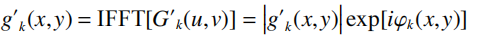
（4）对g'k(x,y)作振幅限制，并将其作为第k+1次迭代的输入光场，继续执行第(1)步。

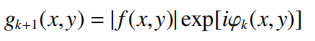
GS算法一般用迭代次数大于特定次数或者损失函数小于特定值作为停止迭代条件，其中第k次迭代的损失函数常用频域的均方根误差EFk2和空域的均方根误差E0k2表示：

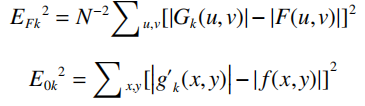
GS算法虽然能够简单有效地恢复出入射光场的相位分布，但是存在着收敛速度慢、容易陷入局部最优解、依赖初始值等问题。为此，研究者们基于GS算法提出了一系列改善收敛性的改进算法。

我国杨国桢、顾本源两位学者提出了非幺正变换系统中振幅和相位恢复问题的一般描述方法——杨顾算法，相较于GS算法适用范围更广。

Fienup在GS算法的基础上对空域的幅值约束作了修改，提出了误差下降（ER）算法，其空域估计值的更新方式为：

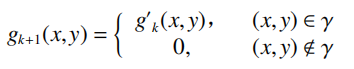
事实上，ER算法只在开始迭代的几个周期内能够较快的收敛，但在后面的迭代过程中收敛缓慢。为进一步加快收敛速度，Fienup在ER算法的基础上引入负反馈机制，提出了混合输入输出（HIO）算法，相比于GS算法同样更改了空域估计值的更新方式：

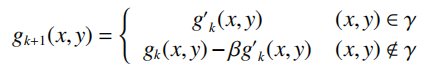
随后，研究人员发现ER算法和HIO算法交替使用能够提升算法的抗噪声能力和收敛速度。由于HIO算法的输入估计值不是输出估计值的连续函数，迭代过程中图像会出现振荡现象。为此，Fienup提出了连续的HIO算法，进一步提高了收敛精度。

除了引入负反馈机制到空域振幅限制，许多研究者提出另一种放松振幅限制的方法——将目标平面划分为信号区域和背景区域，并赋予不同的限制策略，从而有效改善信号区域的图像质量。

除IFTA外，相位恢复问题可以视为一个最优化求解问题，即优化相位分布以实现目标面上辐照度分布尽可能接近于所需的辐照度分布。不同的优化算法相继在衍射光学元件设计领域得到了应用，如模拟退火算法、遗传算法、粒子群算法等。这些算法拥有跳出局部最优解的能力，但收敛速度往往较慢。  

几何光学-物理光学复合设计方法

传统的物理光学设计方法往往都是以随机相位作为优化起点，优化过程中也没有考虑相位的平滑性，导致最终得到的DOE表面常常包含许多高频特征，一方面难以精确加工，另一方面也非常容易受杂散光的影响。同时，随机相位分布包含许多相位突变和相位涡旋，这会使得目标面重建图像出现许多黑点状的散斑。而优化过程中相位涡旋难以自湮灭，导致收敛停滞。

为此，研究者们提出了结合几何光学方法和物理光学方法的复合设计方法，在考虑衍射效应的基础上，尽可能保持DOE表面（或其对应的相位面）光滑。

2005年，Kaempfe等人首先采用迭代网格自适应算法求解了一个平滑的几何光学相位解。之后，用该相位作为 IFTA优化的起点进行迭代，最终优化得到的相位分布比物理光学方法更平滑，同时重建图像质量比几何光学方法更好，体现了复合设计方法的优势。

2015年，冯泽心及其合作者首先数值求解几何光学近似下的蒙日-安培方程（MA）获得几何光学相位分布，随后采用了一种适合光束整形的改进过补偿（MOC）IFTA进一步迭代优化，得到最终的相位分布。该方法由于采用了先进的最优输运求解算法，针对复杂形式的目标面辐照度分布，也可以较为快速地求解出相应的几何光学相位分布。另外，该方法采用的对传统IFTA的过补偿策略可以进一步加快算法收敛速度，提升光束整形质量。图2为冯泽心等人提出的复合设计方法结果：不同方法设计的自由曲面和对应的辐照度分布，其中复合方法（OTMOC）同时实现了表面光滑和图像清晰。

 

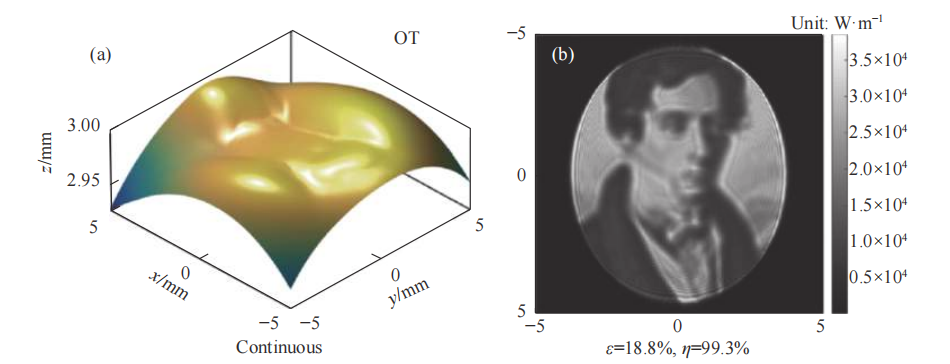
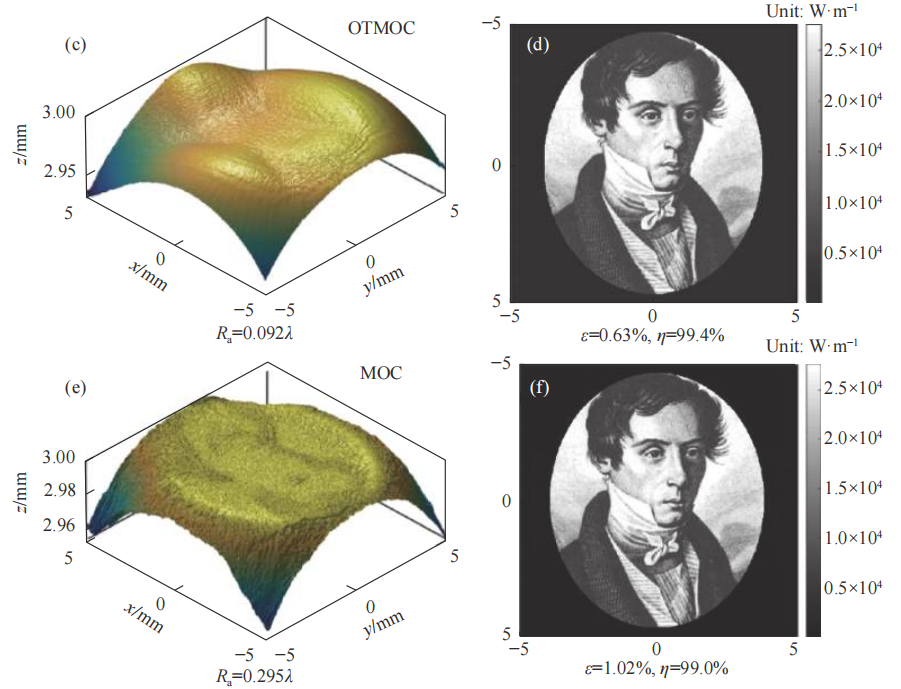
图2（a、b）是几何光学相位分布对应的自由曲面面形和辐照度分布，可见衍射效应会导致整形效果退化；（c、d）是经过MOC算法进一步优化得到的自由曲面面形和对应辐照度分布图，虽然此时曲面光滑度有所下降，但是目标面上的整形效果非常精细，包含了许多细节信息。复合设计方法相比于纯MOC算法（e、f）和GS算法（g、h）整形质量更好，曲面更平滑。

尽管上述复合方法设计得到的几何光学相位是连续的，但并没有控制后续IFTA迭代过程中相位的变化，导致最终优化得到的DOE表面仍然包含一些高频特征。为此，Schmidt等人提出能够严格控制IFTA迭代过程相位表面起伏的复合算法，并将该复合算法应用在自由曲面全息图的设计上，如图3所示。

图3 Schmidt等人利用复合型设计方法设计的自由曲面衍射光学元件将单模光纤出射的高斯光束在远场转化为太极阴阳图光斑

首先采用一种光线映射方法得到全息图几何光学相位分布 φRefr. (x,y)，随后为保持后续IFTA迭代过程中全息图相位的平滑，对迭代过程中相位的变化量φRefr. (x,y)做高斯滤波处理，相位分布的更新方式为：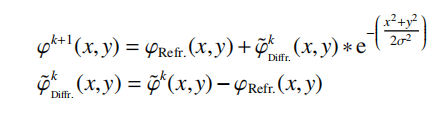

该更新方式保证了IFTA 迭代过程中全息图相位的平滑，同时能够根据加工水平选择合适的平滑权重以控制表面的起伏程度。

类似地，Doskolovich等人提出了结合程函函数求解和IFTA的复合算法。该方法基于费马原理将程函函数求解问题表述为一个最优化问题：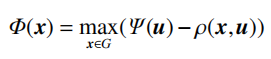

采用梯度下降算法求解了程函函数，进而得到几何光学相位分布。随后，与Schmidt 等人类似，采用了结合高斯滤波的GS算法进行了迭代优化。设计过程中DOE的相位分布和对应的目标面辐照度分布结果如图4所示。

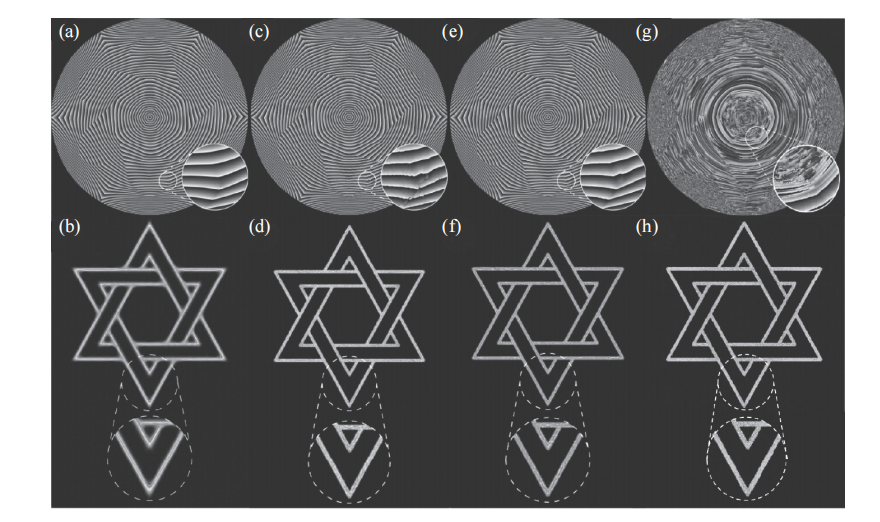
图4 Doskolovic等人提出的复合设计方法。(b)(d)(f)(h)是(a)(c)(e)(g)在目标面上产生的归一化辐射照度分布  

光束整形DOE设计方法发展空间

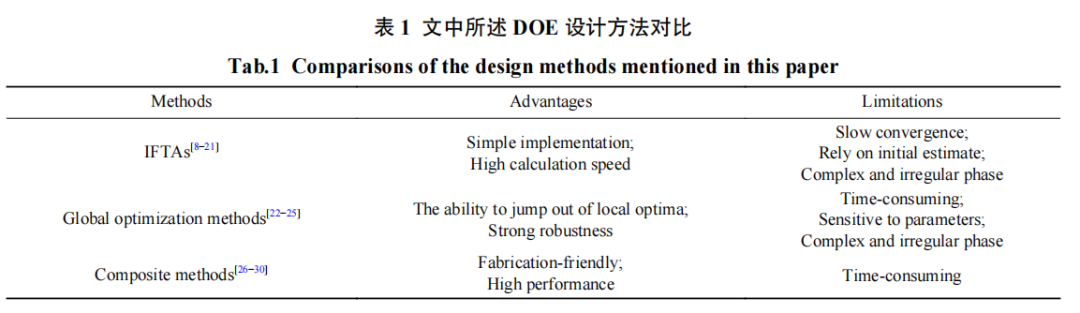
由此可以看到，复合设计方法既能克服几何光学方法忽略衍射效应的缺点，又可解决传统物理光学方法收敛易停滞、相位不规则的问题，能够设计出易于加工、光束整形质量高的自由曲面衍射光学元件。表 1总结了文中所述各类设计方法的优缺点。

 

从科学和工程的角度而言，光束整形DOE设计方法仍具有研究价值和发展空间，存在许多值得探索的方向：

几何光学相位求解过程复杂耗时，需要研究更简洁、更有效的数值求解方法。

研究更快速准确的光场传播模型和数值计算方法，特别是大衍射角场景的衍射计算。

目前DOE的常规加工方式有刻蚀技术、灰度掩膜法、单点金刚石车削技术、激光直写技术等。不同加工方式引起的加工误差有所不同，需要针对特定的加工方式研究对应的加工误差灵敏度低的设计方法，以使加工后的DOE指标最大限度满足设计需求。

除上述复合型设计方法之外，近年来基于物理光传输模型和自动微分技术的梯度下降算法开始应用于相位恢复领域并取得了成功。该方法借助自动微分技术对梯度进行自动求解，体现了灵活高效的特点。如何基于自动微分技术设计易于加工的DOE 也是值得深入研究的方向。

审核编辑：刘清