

光纤传输性能分析:非线性噪声来源简述
电子说
描述
光纤传输性能分析中,应该先确定非线性噪声来源,这是一个基础问题。非线性噪声来源都相对比较复杂,其计算更比较复杂,由于系统的复杂性,一种计算可能只能实用于有限场景,但是不能说该计算是错误的,需要针对具体的场景进行修正或者补充。
非线性噪声的识别有两个比较重要的前提。因为我们考虑的是有效噪声,有些噪声不在信道之内就不算有效噪声,如果噪声完全满足系统的误码率要求,则噪声也可能不必再进行优化而带来成本的增加。
一个是信道的设计,包括信道的带宽和间隔。
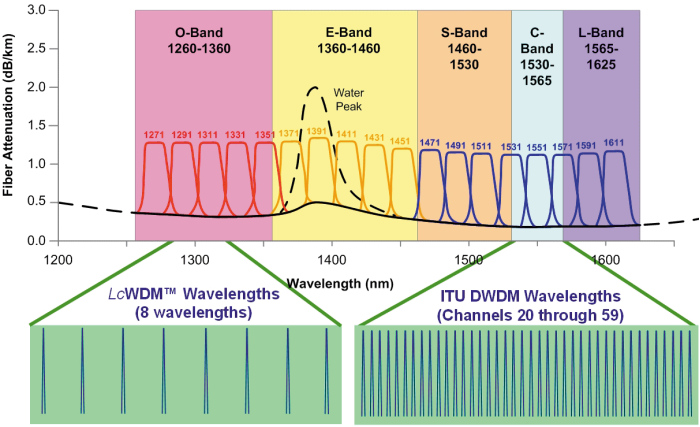
一般情况下,信道的带宽大于等于信道的码率。推荐的奈奎斯特WDM信道,因为其带宽等于信道的码率,信道的间隔可以认为为零。实际上每个信道的带宽可能不一样,间隔也不一致。
非线性噪声的识别是在信道的带宽内进行识别,落在信道的带宽外的噪声自然也没有意义去进行评估。信道占用的带宽大,积累的非线性噪声应该就比较大。信道间隔比较小,信道之间的串扰就比较大,非线性噪声就比较大。从分析角度,最简单的自然是信道间的间隔为零的奈奎斯特WDM信道。频谱效率利用率大致是最高的,分析模型应该是最简单的。
调制格式也应该对非线性噪声带来影响。相同的输入功率,不同的调制格式,其非线性噪声结果也有差异。
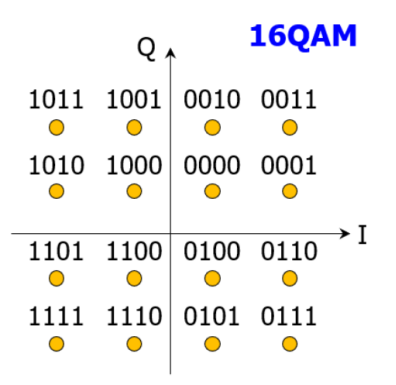
16QAM或者PM-QAM中,取四角的信号振幅,其非线性噪声结果是最高的。取平均功率或许低估了特殊时段的非线性噪声。应该对平均功率和最高功率进行考虑。
非线性噪声是光纤中的非线性效应产生的噪声。目前已知的光纤非线性效应包括五类,受激拉曼散射,受激布里渊散射,自相位调制,交叉相位调制,以及四波混频。但目前非线性效应的分析还是主要集中在四波混频带来的非线性噪声,但是其他非线性噪声来源也是需要进行关注的,特定的应用场景,其噪声或许增大到需要特别关注的程度。
受激拉曼散射和受激布里渊散射源于光脉冲和光纤材料的相互作用,光脉冲和物质之间存在能量的交换。由于目前的放大器配置,长途干线和海底通信中,存在受激拉曼散射和受激布里渊散射带来的非线性噪声。
受激拉曼增益覆盖的频谱能覆盖到40THz,同时受激拉曼散射的噪声也同样覆盖到40THz。
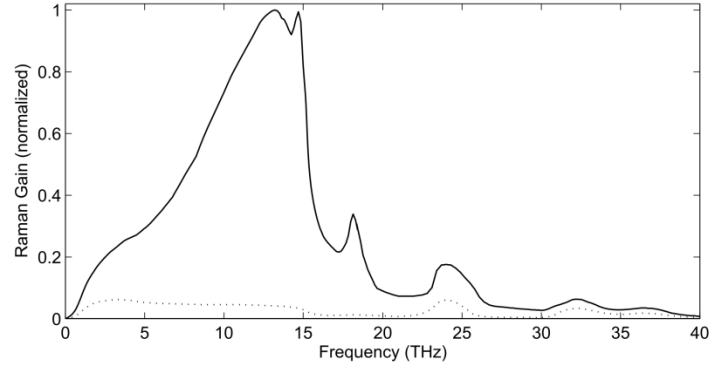
受激拉曼增益在不同的频移下的增益大小,最高增益在13.2THz位置。可以想象出,短波长信道会成为长波长信道的泵浦,这样短波长信道的部分能量会转移到长波长信道而成为噪声。
不过,由于受激拉曼散射的阈值比较高,为1W级别,而典型的信道功率一般1mW。受激拉曼散射对于信道非线性影响应该比较小,其带来的功率代价微小。实际应用中需要考虑各个信道的放大效率和均衡性。
受激布里渊散的阈值比较低(~5mW),需要考虑其带来的噪声,但是主要是前向布里渊散射(前文:光纤非线性特性-布里渊散射),虽然该影响确实也比较小,但是在系统评估中不应该被忽视。值得一提的是,由于光纤的优化,一般受激布里渊散的阈值也提高了很多个dB。这个要看具体的光纤性能。
自相位调制,交叉相位调制,以及四波混频,源于信道中光脉冲之间的相互作用,能量交换发生在光脉冲频率之间,并不和材料物质相互作用。
自相位调制和交叉相位调制带来的是相位噪声,四波混频应该属于振幅噪声。四波混频发生的能量交换均处理为噪声,但是有一点,如果产生的新频率的光子和该频率所占用的信道的信号光子巧合同频同相同方向同一个时刻位置,应该会起到放大作用。但是这种概率比较低,从分析角度上,四波混频产生的新频率的光子均处理为噪声。
如果存在自相位调制,则其光波相移在线性相移的基础上增加了非线性相移:
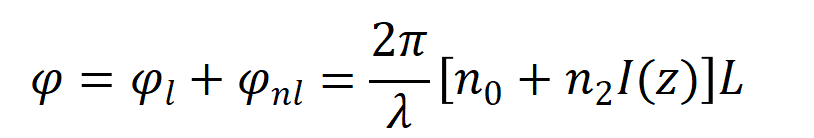
根据光场的表达式,就有(非严谨的数学表达,但是逻辑上是严谨的)
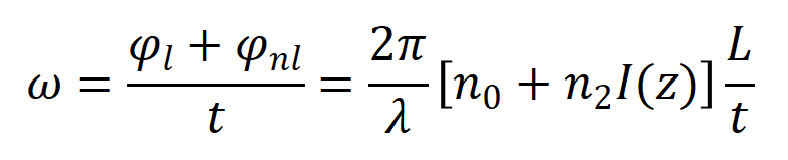
则第一个公式可以看到自相位调制带来了非线性相移,第二个公式中看到自相位调制也扩展了频谱。频率扩展其中一种情况是形成光孤子带来增益,一种情况脉冲在时间域上扩展形成相位噪声。
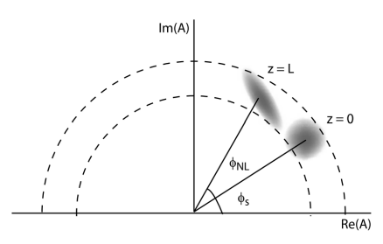
在光脉冲传播距离L后,自相位调制引入的相位噪声逐渐增强,最初的圆形功率分布信号变成一个椭圆功率分布信号。但是振幅波动的范围没有受到影响。
交叉相位调制带来的相移远大于自相位调制:
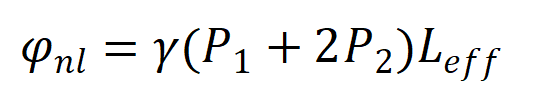
如果参与交叉相位调制两个频率功率相等,则非线性相移将是自相位调制的三倍。
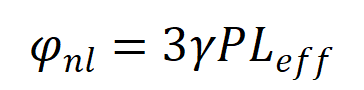
可以预知,其相位噪声也存在很大的增强。交叉相位调制的相位噪声也是分析的一个重点。
在目前的非色散补偿方案中,随着系统数字处理技术的增强,相位噪声被证明影响比较小。非线性噪声主要集中在四波混频上。
四波混频的高效率需要满足能量守恒和动量守恒。能量守恒和频率有关,动量守恒则和传播常数或者相位相关。能量守恒确定了四波混频会产生那些新的频率。动量守恒决定四波混频的效率,即最大四波混频效率需要参与四波混频的四个传播常数差等于零。
假定四个频率等间隔,则每个传播常数按泰勒级数展开后取其差值,有
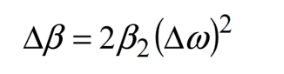
则可以看到二阶色散系数或者群速度色散beta2等于零时,传播常数差等于零,这时,四波混频的效率最高。也就是在光纤的零色散位置附近,四波混频的效率最高。远离光纤的零色散位置,则四波混频的效率就比较低。
四波混频中四波前面的符号只存在或者只考虑下面的关系,其他的符号或者不可能存在,或者不在通信频谱的范围之内。
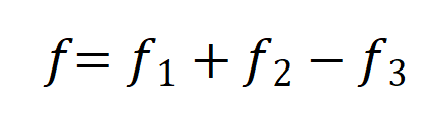
由f1,f2,f3频率参与的非线性过程而转移到新频率f上的功率将视为四波混频效应导致的噪声。由于有效的功率密度谱只存在有效带宽上,f1,f2,f3也落在有效带宽,并且原则上要遍历整个有效带宽,而忽略掉中间的带宽间隙,这样四波混频效应导致的噪声最初应该需要三重积分。如果以Hz为单位,则一个32GHz的信道就存在数量可观的参与四波混频的频率,而新频率也可能落在任何信道,或者落在信道之间的间隙。
如果每个信道的功率均等,很容易知道,中间的信道的中心频率其四波混频效应最强烈,而其噪声也最大,是考虑的重点。由于前面的频率关系,可以预知,如果考虑中心频率f,则其他三个频率可能来在1)全部来自中间信道;2)来在中间信道和另外一个信道;3)来自三个信道,这三个信道或者包括中间信道,或者是非中间信道的其他信道。
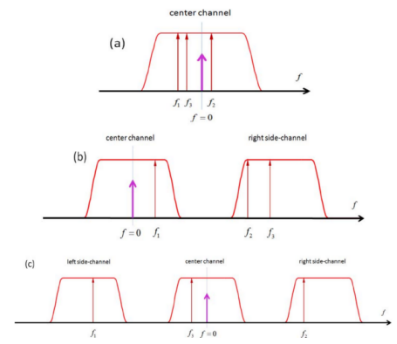
而不同的频率其四波混频效率也有不同,考虑四波混频效率,注意,由于可以设置f=0,则f3是f1和f2的和。
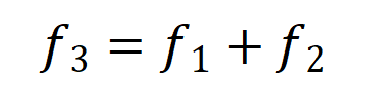
所以三重积分可以减少到二重积分。
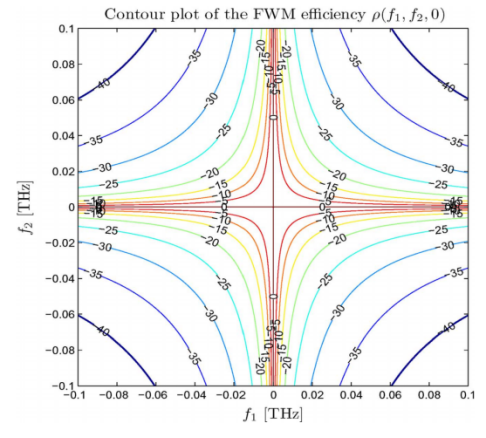
四波混频效率图示中看出,重点考虑的场景是:其中一个频率位于中间信道,如果两个频率均不在中间信道,则其四波混频效率急速下降。
总之,目前明确的非线性噪声来源:
四波混频带来新的频谱噪声,应该属于振幅噪声。
自相位调制和交叉相位调制带来相位噪声,如果系统无法有效补偿其功率代价,其中交叉相位调制带来的相位噪声需要进行考虑。
前向布里渊散射带来噪声是一个基础噪声,基数较低,但是需要考虑。
拉曼散射带来的噪声,大多数分析都被忽略,但是需要进行分析确定是否可以忽略。
审核编辑:汤梓红
-
利用对称非线性光纤环镜产生多波长激光的研究2010-04-24 0
-
功率、增益、噪声和非线性2010-10-02 0
-
光载无线通信系统的抵抗色散及非线性效应的性能分析2019-06-17 0
-
非线性电阻威廉希尔官方网站 分析2008-12-04 911
-
非线性威廉希尔官方网站 的分析方法2010-09-25 619
-
基于小波神经网络的非线性噪声对消2012-05-07 867
-
实现线性传输的非线性光电耦合威廉希尔官方网站 的设计与仿真2018-04-13 1147
-
相敏放大器减少光纤传输中受到噪声和非线性效应信号失真的影响2018-07-10 2562
-
使用超低噪声放大器可以实现4000km的光纤传输链路2018-08-16 1019
-
实现线性传输的非线性光电耦合设计与仿真2021-06-21 744
-
评估光纤传输的容量2022-09-02 2532
-
非线性功率放大器对QAM传输BER性能的影响及补偿2023-02-17 249
-
射频中的非线性是什么 射频设计中无源互调的来源是什么?2023-07-28 949
-
简述噪声的产生机理和来源2023-08-22 1879
全部0条评论

快来发表一下你的评论吧 !

