

飞行控制PID算法的作用解析
描述
PID控制器是一种线性控制器,它主要根据给定值和实际输出值构成控制偏差,然后利用偏差给出合理的控制量,目前,人们通过科学研究获得了诸多具有优异控制效果的算法和理论,但在工程应用领域,基于经典PID的控制算法仍然是最简单、最有效的控制方案。目前主流的几款开源飞控中,无一例外地都是采用PID控制算法来实现无人机的姿态和轨迹控制。
那么PID控制器算法能解决什么问题呢?以多旋翼为例,在没有控制系统的情况下,直接用信号驱动电机带动螺旋桨旋转产生控制力,会出现动态响应太快,或者太慢,或者控制过冲或者不足的现象,多旋翼根本无法顺利完成起飞和悬停动作。为了解决这些问题,就需要在控制系统回路中加入PID控制器算法。在姿态信息和螺旋桨转速之间建立比例、积分和微分的关系,通过调节各个环节的参数大小,使多旋翼系统控制达到动态响应迅速、既不过冲、也不欠缺的现象。
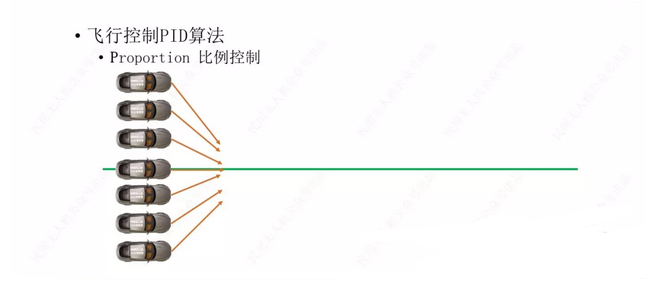
下面我们简单的举个例子让大家了解一下PID的作用,我们先以一个自动驾驶的小车来举例子,为什么用小车呢而不用多旋翼来举例子呢?因为用小车举例,可以看到小车的行进轨迹,根据轨迹我们可以很直观的看到PID对控制的影响,便于理解PID的作用。
我们先讲P,比例控制。现在我们想让这个小车沿着绿线向前走,我们给P设置一个固定的值,这个值可以让离开绿线的小车向绿线的方向行驶,离的越远,方向盘打的角度越大,离的越近,方向盘打的角度越小。橙色的箭头表示小车行进的方向

比如这个小车在这个位置,我们设置了一个中等大小的P值,想要沿着绿线走,在比例控制下路径是这样的,因为小车有一定的速度,到达绿线时因为惯性的原因又向前运动了,然后再根据中等P值向回打方向盘,当到达绿线时,同样因为惯性的原因冲过了头,因为小车越接近绿线,方向盘打的越小,所以小车每经过一次绿线,它的偏差就越来越小,所以随着小车多次的往复运动,就能离绿线越来越近,理论上最终能够行驶在绿线上面。
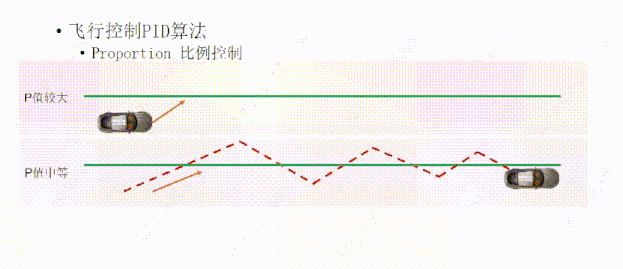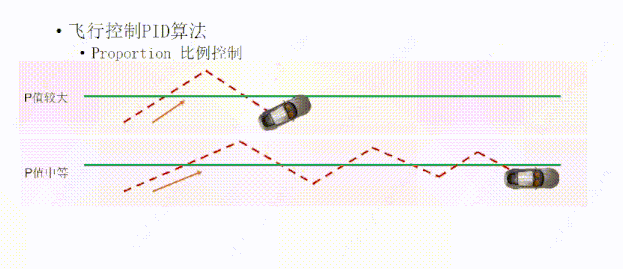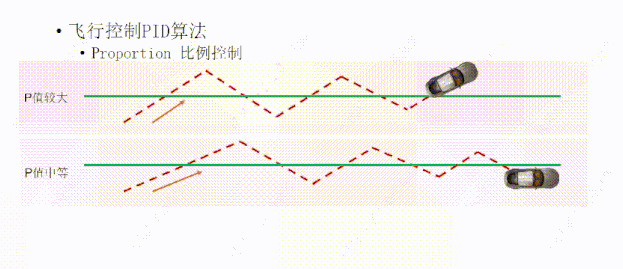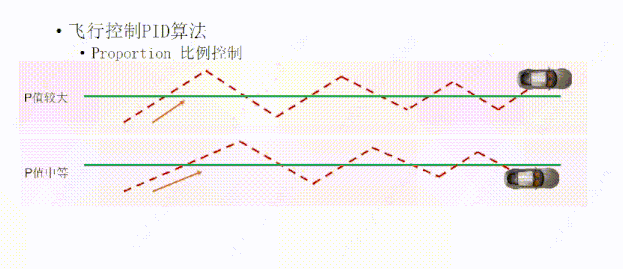
如果我们把P值设置的比较大,它的路径是这样的,因为方向盘打的角度比较大,所以小车比中等P值的时候较早的到达绿线,但同样因为惯性的原因会多次往返绿线的两侧,也是一次比一次接近绿线,因为它方向盘角度打的比较大,所以会比中等P值往返的次数要多,最终经过多次往返,理论上它会离绿线越来越近,最终到达绿线上方。
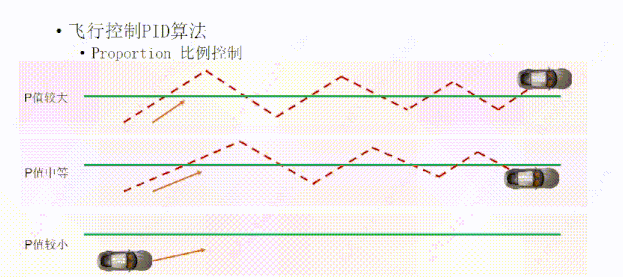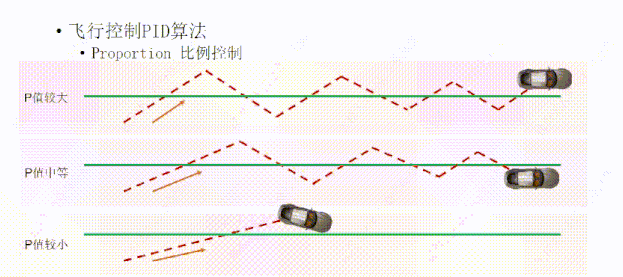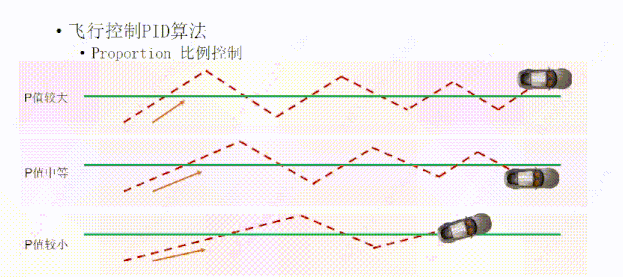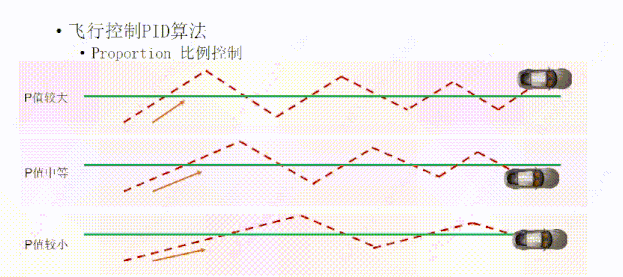
如果我们把P值设置的比较小,也就是方向盘打的角度比较小,它的路径是这样的,小车会较晚到达绿线,因为惯性会往返绿线两侧,但是因为方向盘角度小,小车可以在较少的往复次数下接近绿线。
所以我们对比一下设置这三种P值的结果,在小车与绿线相同距离的情况下,P值越大,小车的反应越快,P值越小,小车的反应越慢,所以这三个小车第一次到达绿线的时间是不一样的。虽然P值大能够较快的到达绿线,但是反应比较剧烈,总是因为过快冲过了头。相反P值小的反应比较平缓,但是它反应太慢,我们有时候接受不了。
什么样的P值是合理的呢,就是设置后,小车的反应不是很剧烈,反应时间你也能够接受,那这就是一个相对合理的P值。
那有没有一种办法让它反应再快一点,反应又不那么剧烈呢,那就要用到接下来我们要讲的微分控制了。
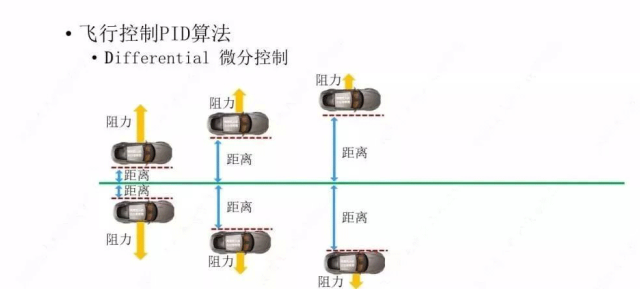
我们为了不让这个小车冲过头,我们再给它加一个力,这个力就是D,让这个力来起一个作用,就是让小车越接近绿线的时候,接近绿线的速度越慢,小车越远离绿线的时候,接近绿线的速度相对较快,这个接近绿线的速度不是小车前进的速度,是小车与绿线平行线之间的相对速度。这个D大家可以理解为小车靠近绿线的一个阻力。

假设我们设置了一个相对合理的P值,在P值不变的情况下,微分控制中D值的变化会有怎样的结果。比如我们设置了一个比较合适的D值,微分控制(D)让小车在靠近绿线时,接近绿线的速度比较慢,这样比例控制(P)就可以很轻松的让小车到达绿线上方行驶。
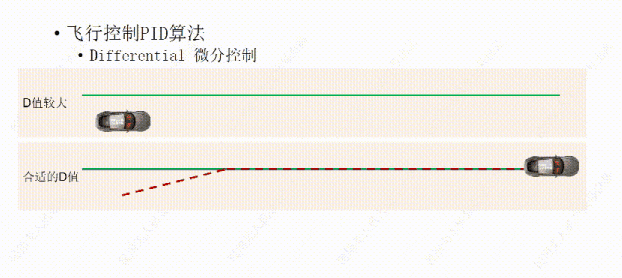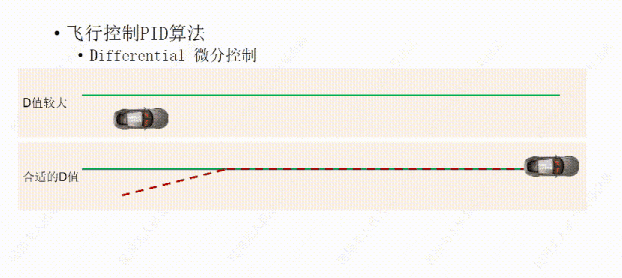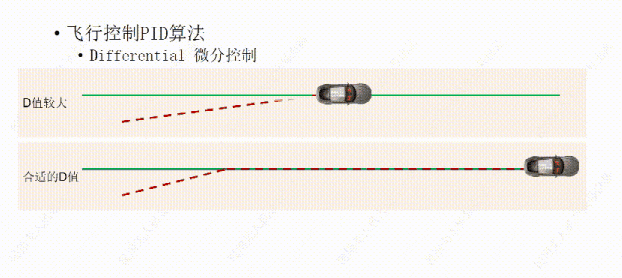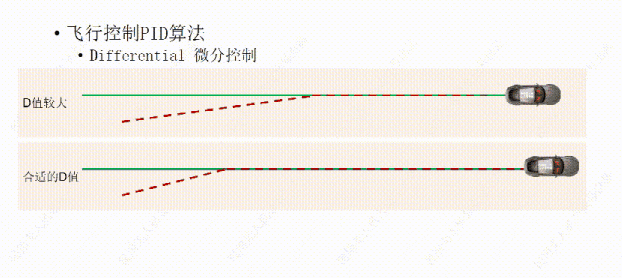
如果D值过大,也就是小车靠近绿线的阻力过大,这样会让小车需要比较长的时间才能到达绿线上方。

如果D值设置的过小,也就是小车靠近绿线的阻力过小,那微分控制(D)就不会对比例控制产生大的影响,所以虽然小车能够较快到达绿线,但小车需要多调整几次,在绿线的两侧往复几次后才能到达绿线上方行驶。
那这样看来比例控制(P)和微分控制(D)的配合,貌似已经很完美了。为什么还要有积分控制(I)呢?
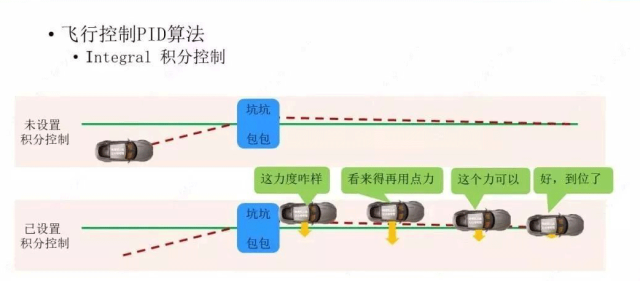
设置合适的P值和D值,可以让小车很好的沿着绿线一直走,但路上不是很平坦,会有些坑坑包包,或者其他的一些干扰,路况不好就会让小车的行进路线发生偏移,比如小车在这里遇到了坑坑包包,它的行进路线就会变成这样,稍微偏离了绿线一点,因为微分控制(D)让小车离绿线越近时,靠近绿线的速度越慢,比例控制(P)让小车在接近绿线时,方向盘又打的比较小,所以小车要走一段路才回到绿线上面。
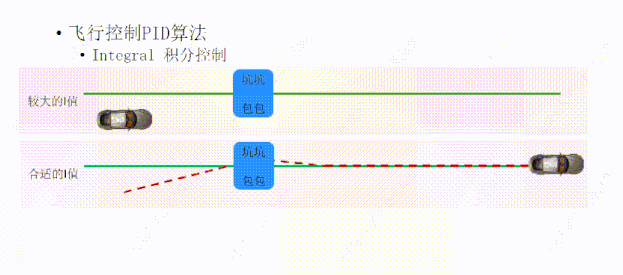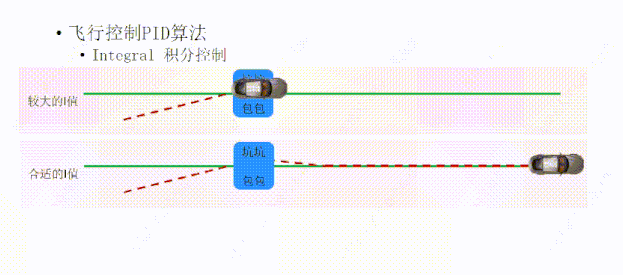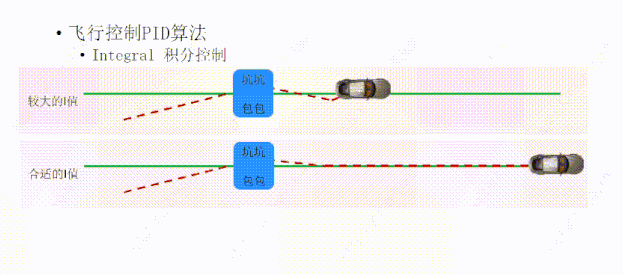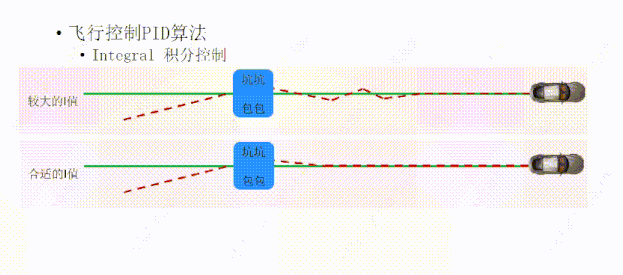
有没有办法让它更快回到绿线上面呢,所以我们再给它加一个力,这个力就是I,积分控制。我们让积分控制起这样的作用:如果P和D的调节不是很理想的话,就让I帮他俩一把,向P的方向上加一个力,这样可以让小车更快回到目的路径。
设置了I以后,I会根据误差和误差经历的时间进行积分,然后决定施加给目标方向的力的大小,就能够让小车回到目标轨迹上。
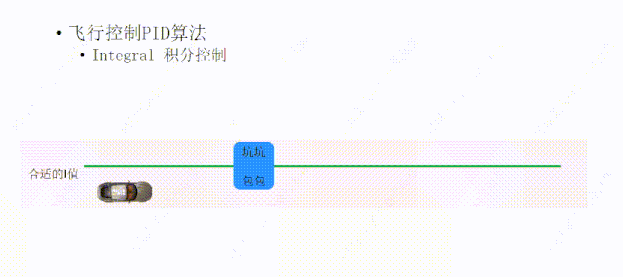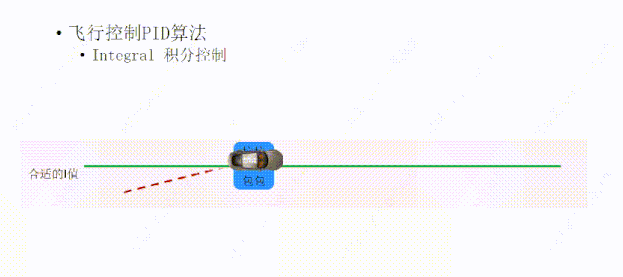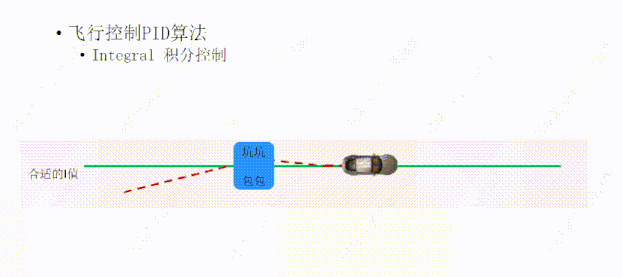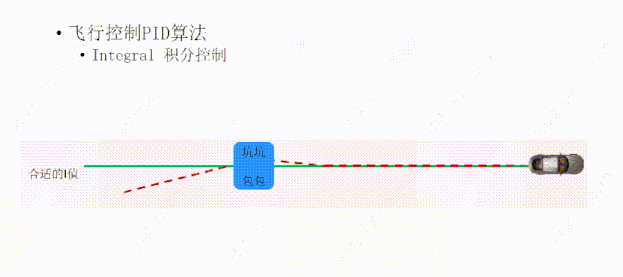
一个合适的I值,可以让小车偏离轨迹后,I可以在合适的时间给P一个合适的力,让小车快速的回到绿线上面;
如果I值过大,积分控制(I)调整的力就会比较大,它在帮P的时候会用力过猛,会让小车冲过绿线,下次帮忙的时候还是用力过猛,P表示很无奈,毕竟I也是好心,经过几次调整后,小车终于回到绿线上面,但我们看小车的轨迹线产生了一定的振荡;
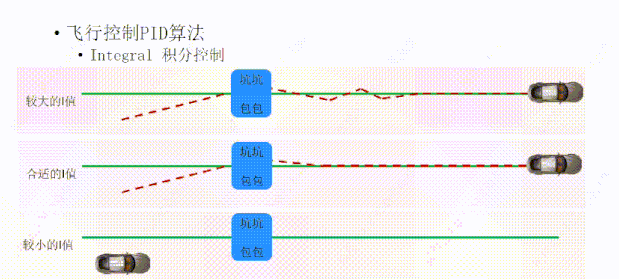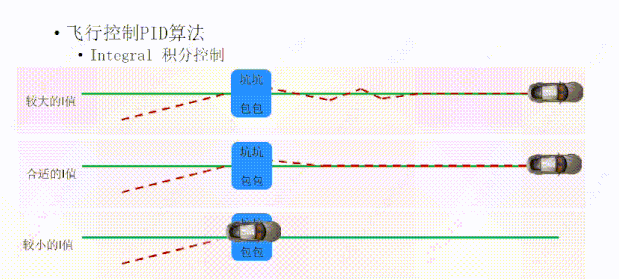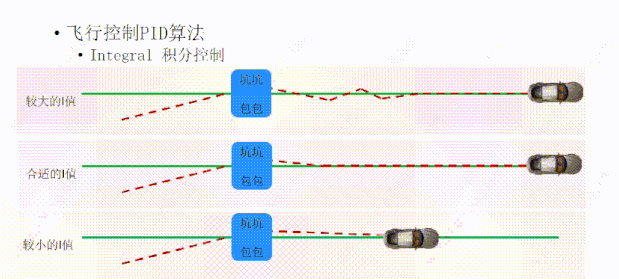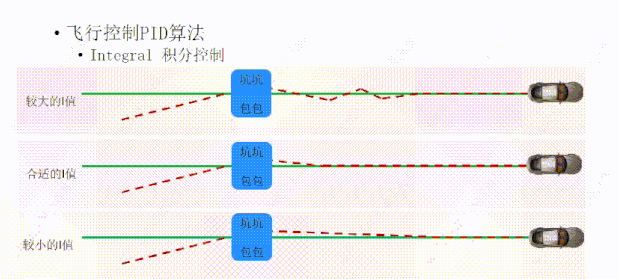
如果I值过小,积分控制(I)调整的力就会比较小,就像有一个手无缚鸡之力的柔弱小鲜肉一样,帮不上太大的忙,所以小车回到正确轨迹的时间就会比较长。
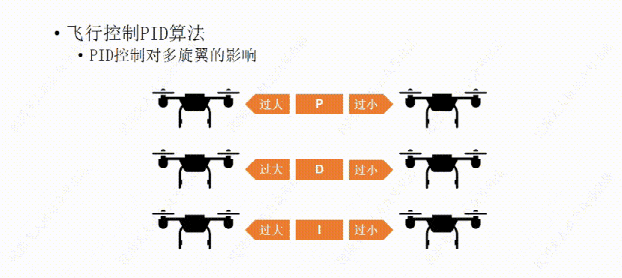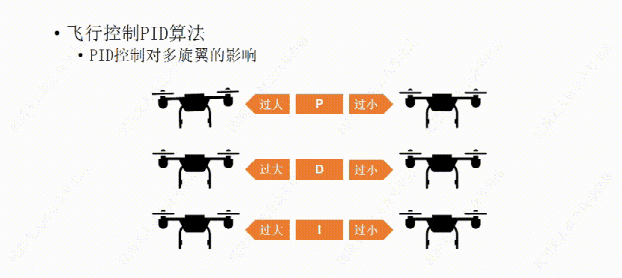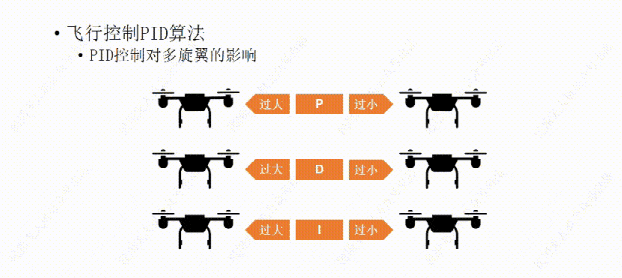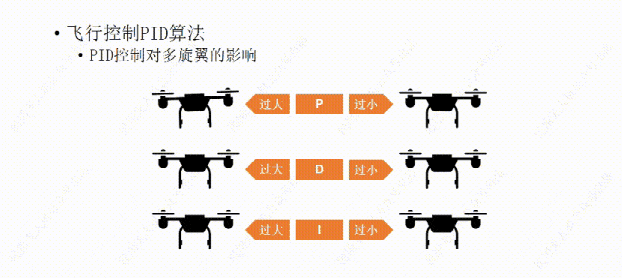
说完了PID控制对小车的影响,下面我们再说说PID控制对多旋翼的影响。比如这架多旋翼想要作的是保持机身的水平平稳。
我们先从P开始,如果P值设置的过大,哪怕机身有那么一丁点倾斜,飞行器都会用稍大一些的力去调整,结果用力过猛,又继续向回调整,这样飞行器就会频繁的调整自己的水平状态,导至机身产生振动。
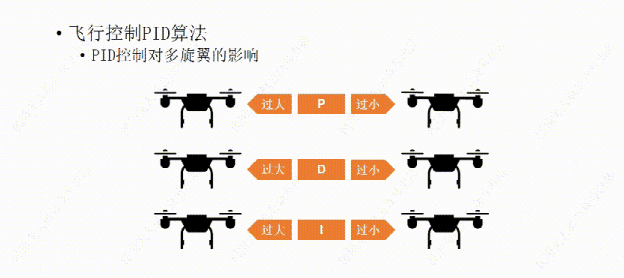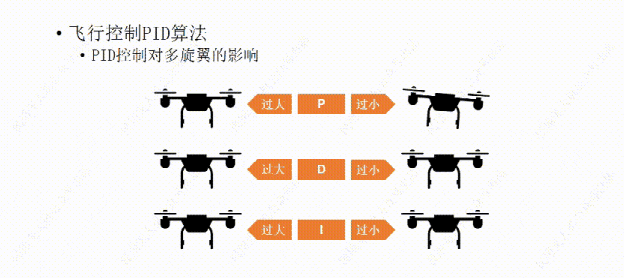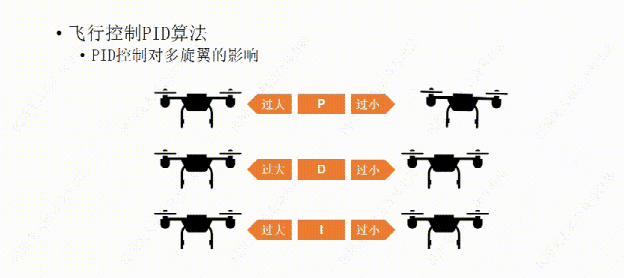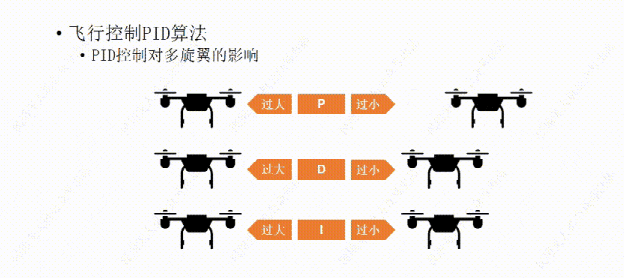
如果P值设置的过小,飞行器的水平调整就会显得力不从心,比如空气中的微风让飞行器发生了倾斜,飞行器向回调整的力比较小,所以需要长一点的时间才能调平,这样让我们觉得它反应有点慢。
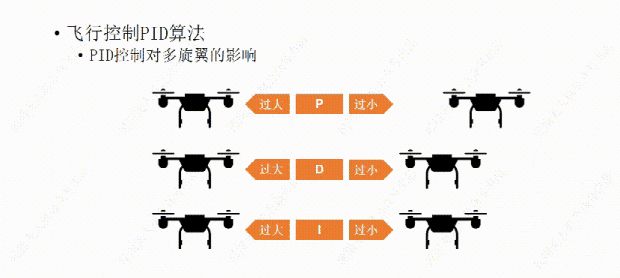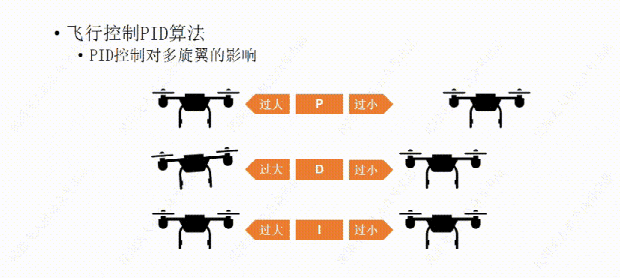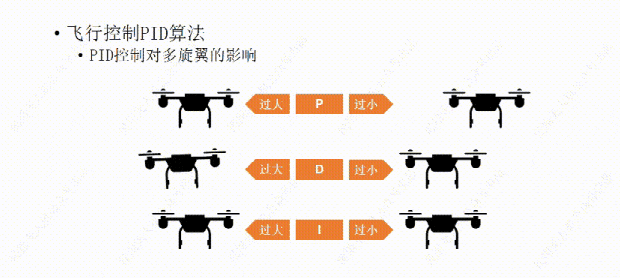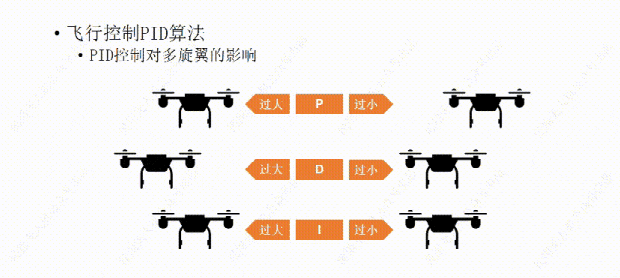
比如我们经过多次测试设置了一个比较合适的P值,可以让飞行器有一个我们能接受的反应时间,但稍有一点过冲,会有一些震荡,接下来再设置D值,让D值消除震荡,如果D值设置过大,会让飞行器恢复平衡时间过长,反应变慢,
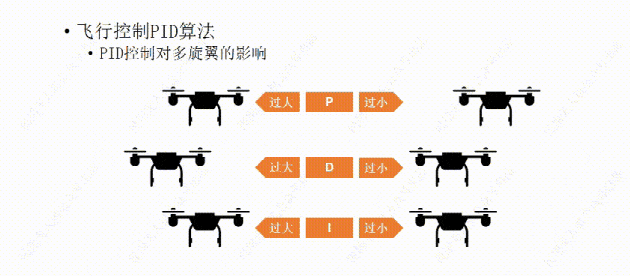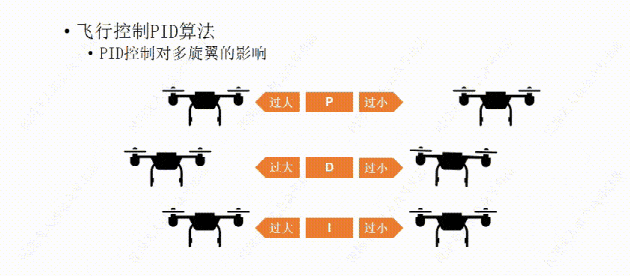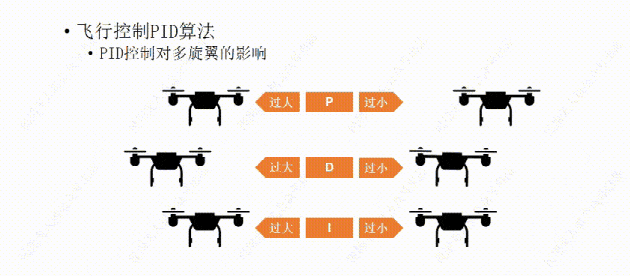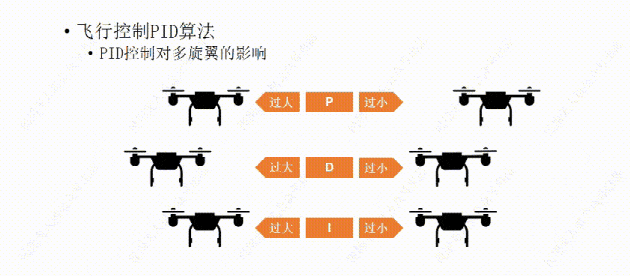
如果设置了一个过小的D值,会导致效果不明显,飞行器还是会有震荡。
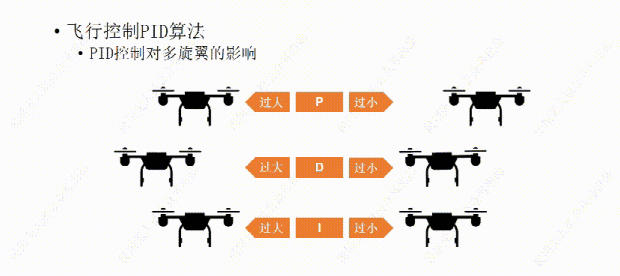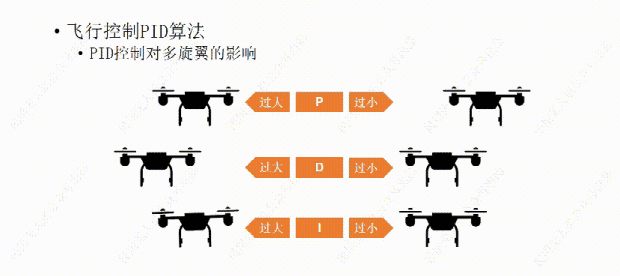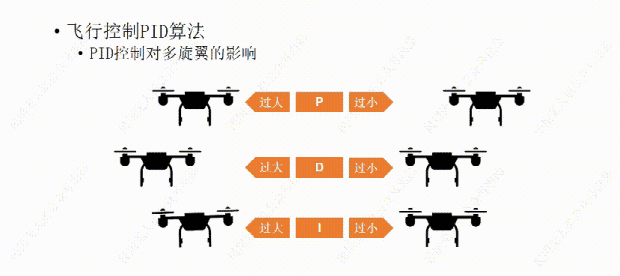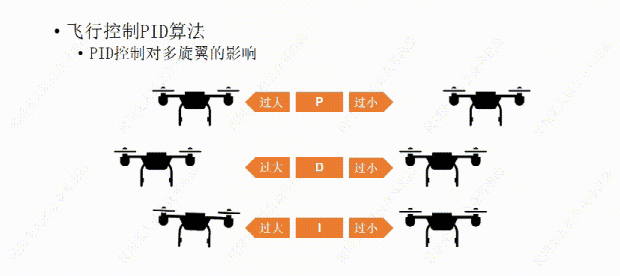
比如我们又设置了一个合适的D值,可以让飞行器反应不是很慢,也不会有明显的震荡。接下来我们再设置一下I值。这里的I我们可以这么理解,I根据飞行器的反应时间,适当的帮忙,如果飞行器反应慢了,他就会帮一下,能让它的反应快一点。但是如果值设置的过大,这个帮忙可能会用力过猛,导致过冲。
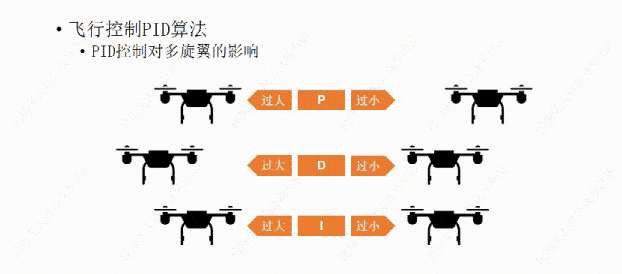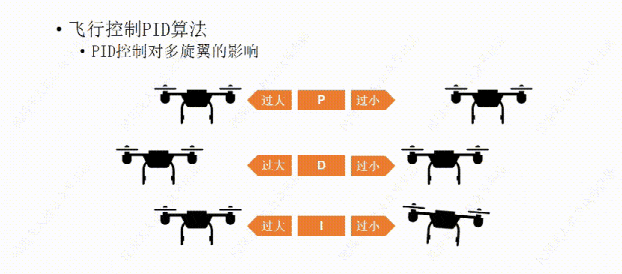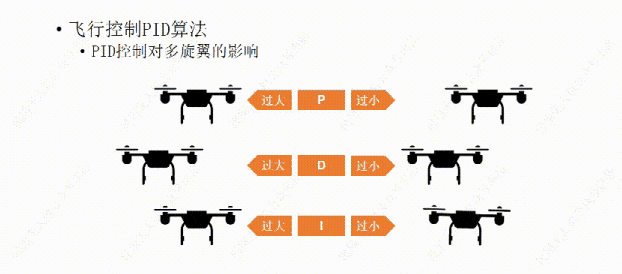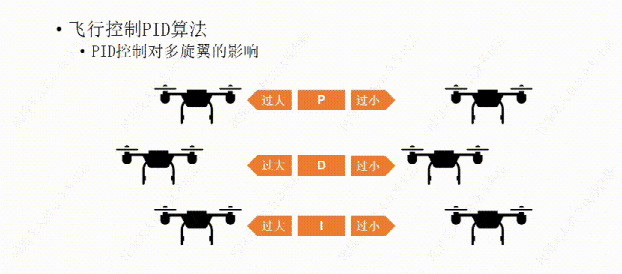
如果I值设置过小,它的帮忙就没有太大的作用,还是不会让飞行器反应更快。所以设置一个合适的I值需要多次的测试,让它的帮忙起作用,又不会用力过猛。有些人怕麻烦就不设置I值了,其实也没有太大的影响,只不过离完美还差那么一点。
PID的设置是一个非常复杂的过程,对于一般的使用者来说是非常难的。所以有些厂商也想出了一些办法。

比如3DR的开源飞控APM和PIXHWAK,咱们看它的调参软件中,PID部分有这么多要调的地方,对于一般的用户来说是比较有难度的,所以它加了一个自动调参的功能,就是这个AutoTune,可以把遥控器上的一个开关设置成自动调参,找一片开阔地让飞行器起飞,然后把遥控器上的自动调参开关打开,飞控就开始自己控制飞行器进行飞行测试,然后根据测试情况自动设置一个比较合适的PID参数。

有些厂商作的就更简单了,直接在调参软件里加了一个感度的配置,这个感度大家可以理解为敏感度 ,数值越大,敏感度越高,不同的轴距都有不同的推荐感度设置。
左面的这个是大疆NAZA飞控的调参软件,调参软件说明书里就有一个不同轴距的推荐感度值,右面的拓攻更简单,直接选择轴距,就能自动设置推荐的感度值。
这些厂商的调参软件里一般都会有姿态感度和基本感度,或者叫稳定感度。姿态感度是指飞行器对遥控指令的敏感程度,基本感度或稳定感度是指飞行器对于外界干扰反应的敏感程度。这样就比PID理解起来要简单的多了。
审核编辑:汤梓红
-
初步解析飞思卡尔控制电机PID算法代码2014-11-04 0
-
PID控制算法【精】2015-12-28 0
-
四轴飞行器的PID算法2016-01-15 0
-
四轴飞行器控制器的秘密——PID算法大解析2019-05-30 0
-
介绍一种基于四轴飞行器的双闭环PID控制算法2021-05-19 0
-
什么是PID控制算法?PID控制算法C语言是如何实现的?2021-06-29 0
-
PID算法有哪些应用2021-07-15 0
-
PID算法的解析,绝对实用2022-01-21 0
-
什么是PID控制算法呢?PID控制算法有何作用2022-02-25 0
-
pid算法_什么是pid算法2012-01-01 11221
-
PID控制算法控制算法2016-11-17 908
-
改进PID的无人机飞行姿态角控制消颤算法_陆兴华2017-03-19 937
-
四轴PID控制算法详解(单环PID、串级PID)2017-08-29 1697
-
PID控制算法的C语言实现2022-01-13 1017
-
什么是pid控制,其控制作用是什么2024-02-01 2394
全部0条评论

快来发表一下你的评论吧 !

