

功率模块铜线键合工艺参数优化设计方案
描述
胡彪 成兰仙 李振铃 戴小平
(华南农业大学 湖南国芯半导体科技有限公司湖南省功率半导体创新中心)
摘要:
为了提高功率模块铜线键合性能,采用6因素5水平的正交试验方法,结合BP(Back Propaga‐tion)神经网络与遗传算法,提出了一种铜线键合工艺参数优化设计方案。首先,对选定样品进行正交试验并将结果进行极差分析,得到工艺参数对键合质量的影响权重排序。其次,运用BP神经网络构建了铜线键合性能预测模型,并通过遗传算法对BP神经网络适应度函数求解,得到了工艺参数的最优值。将BP-遗传算法与传统优化方法的优化结果进行对比,发现经BP-遗传算法优化后的铜线键合工艺稳定性提升更加明显。最后,对功率模块进行了功率循环试验,结果表明经BP-遗传算法优化后的模块功率循环能力得到显著提升。
0 引言
功率模块引线键合技术是指模块内部硅基芯片或SiC芯片与陶瓷衬板间,以及陶瓷衬板与功率端子间的电气互连技术 [1] 。随着功率模块的电流密度不断提高,传统粗铝线在通流能力与耐温能力等方面都难以满足封装要求,具有更强通流能力的铜线凭借其自身优异的力学和热学性能,受到了业界的极大关注 [2] 。
对于功率模块引线键合质量与性能的相关研究,目前主要运用的是基于试验与仿真的方法。文献[3-5]通过对粗铝丝进行键合试验,得到了超声功率、键合压力、键合时间3个工艺参数,以及这3个参数与键、性能之间的影响权重关系;文献[6]采用极差分析法对功率模块芯片区域的第一键合点与第二键合点进行系统研究,确定了粗铝线键合的最优工艺参数;文献[7]运用响应面法 (response surface methodology,RSM)进行数据建模,得到了优化后的超声楔形焊工艺参数。近年随着深度学习被广泛应用在各学科领域,基于数据的方法开始出现在功率模块引线键合研究中,这类方法目前主要应用于功率模块引线键合的失效分析与模块寿命预测中,在铜线键合性能研究中的应用仍不常见。文献[8]使用基于神经网络的键合线状态评估方法,对IGBT模块键合线故障进行在线监测,有效地提高了功率模块的可靠性;文献[9]基于改进后的小波神经网络建立了IGBT时间序列预测模型,对评估IGBT运行状态与预测剩余寿命提供了支持。分析国内外相关研究可以发现,针对引线键合的工艺研究一般基于极差分析或RSM等传统方法,然而随着试验水平数量与试验次数的增加,该类方法得到的优化工艺值准确度偏低,不利于实际生产。
为了更好地对键合工艺参数进行优化,提升功率模块铜线键合性能,本文以6因素5水平的正交试验为基础,采用BP(Back Propagation)神经网络预测和遗传算法反向求解铜线键合点最优键合工艺参数值,为功率模块铜线键合的工艺参数优化设计提供了一种新方法。将传统优化方法与“BP‒遗传算法”进行优化结果对比,“BP‒遗传算法”对键合工艺稳定性的提升明显;对功率模块进行功率循环试验,发现随着超声功率的不断优化,模块功率循环寿命也得到显著提高。
1 正交试验
1.1 试验材料及设备
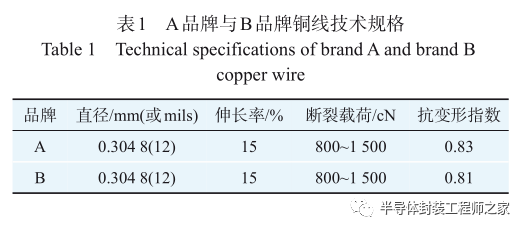
在本次试验中,键合铜线分别采用A品牌与B品牌,技术规格如表1所示。衬板采用AMB(Active Met‐al Bonding)衬板,外形尺寸(长×宽×厚)为28 mm×26 mm×0.92 mm [0.3(Cu)/0.32(ceramic)/0.3(Cu)];铜箔采用DTS(Die Top System)铜箔,尺寸为4.2 mm×2.8mm×0.1 mm。试验选用全自动引线键合机进行铜线键合,搭配推拉力测试仪对铜线键合强度进行测试。
1.2 试验及结果
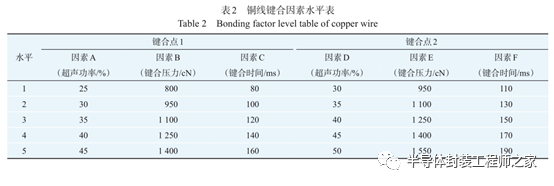
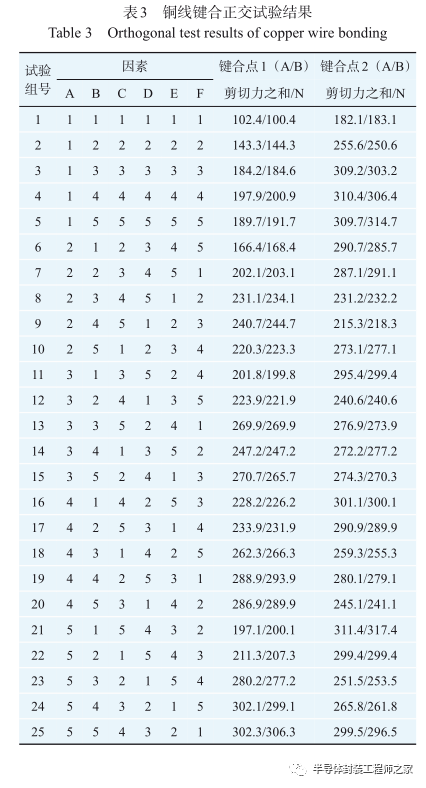
相比于铝线键合,铜线键合的工艺参数设置整体偏大。因此,在进行键合工艺前,需要先在功率芯片表面烧结1层DTS铜箔,避免劈刀与芯片的直接接触。图1为使用DTS工艺的键合点示意图,由于键合位置的不同,分别标记为键合点1与键合点2。根据DTS工艺中铜线键合参数的经验值,分别列出键合点1与键合点2因素水平表,如表2所示。将本试验所确定的因素水平进行分析,设计6因素5水平共25组试验的正交试验方案,同时为了减小偶然因素与试验方法带来的误差影响,规定每组工艺参数组合进行10次重复试验 [10] ,共计得到250组试验结果,作为后续分析的样本数据。25组样品经过10次重复试验得到的键合点剪切力之和,作为功率模块铜线键合正交试验的结果,如表3所示。

1.3 极差分析法
对正交试验的结果进行极差分析,极差值R越大,表明该因素对试验结果的影响越显著,该因素为主要因素;极差值R越小,表明该因素为次要因素。A品牌与B品牌的铜线键合点剪切力均值与极差响应分析结果分别如表4所示。由表4可知,2种品牌的铜线键合试验结果具有一致性,影响单一键合点剪切强度的主要因素皆为该点的超声功率、键合压力与键合时间,其中超声功率对剪切强度的影响最为明显。
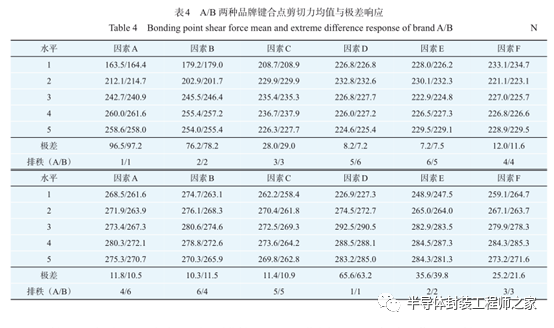
由极差分析结果可得出2种品牌铜线的最优键合参数组合:对于键合点1,最优工艺参数组合为A4B4C4;对于键合点2,最优工艺参数组合为D3E4F3。
2 工艺参数优化
2.1 剪切力预测模型
本文所建立的 BP 神经网络采用双隐含层的结构 [11-13] 。最佳隐含层节点数的选取如下:
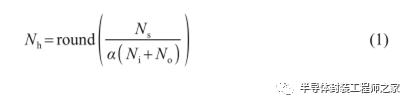
式中: N h 为隐含层节点数; N s 为训练集中的样本数;N i 为输入层节点数; N o 为输出层节点数;α的取值范围通常为2~10;round( )表示取整。
在工程中,一般先由式(1)确定隐含层节点数的大致范围,再采用试凑法确定隐含层最佳节点数。如将输入层节点数6、输出层节点数2和样本数250代入式(1),用试凑法确定的最佳值为9 [14] ,由此得最佳隐含层节点数为10。
为了避免输入数据之间存在不同量级而导致误差波动,本文对训练样本进行了归一化处理 [15] ,具体计算如下:

式中:x为归一化后的数据; x m 为某个输入参数的实际值; x min , x max 分别表示训练集中此参数的最小值和最大值。
均方误差(Mean Square Error,MSE)函数可以较为精准地反映预测值与实际之间的估计量,因此选择将BP神经网络的损失函数确定为MSE函数,如下所示:
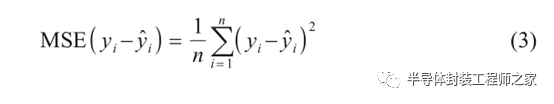
式中:n为样本总数;y?i 为样本i的预测值; y i 为样本i的实际值。
由于A、B这2种品牌铜线键合点的剪切力与极差分析结果具有一致性,为了减少运算量提升运算速度,只选取其中1组数据进行BP神经网络建模分析。选择A品牌铜线键合点1与键合点2的超声功率比、键合压力和键合时间作为BP神经网络的输入,键合点1与键合点2的剪切力值作为BP神经网络的输出,可建立如图2所示的6×p×q×2的BP神经网络,其中p和q为隐含层1和隐含层2神经元的数目。
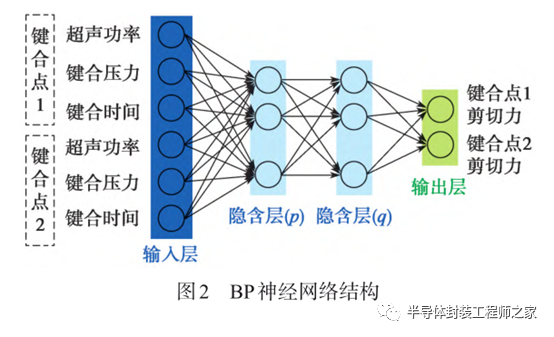
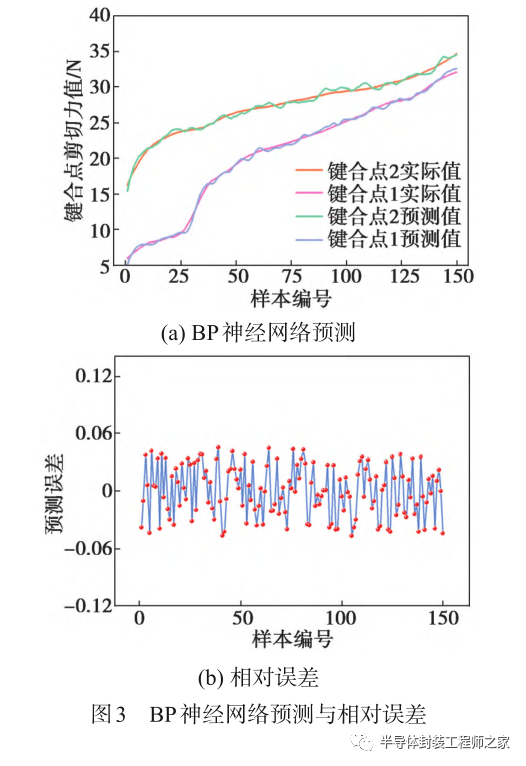
图3为BP神经网络预测图与相对误差图,其中最大相对误差不超过4.7%。训练完成后的BP神经网络具有较高的预测性能,可通过任意输入工艺参数值较为准确地预测键合点的剪切力值,既能有效地检验键合设备的运行工况,及时对磨损的劈刀进行更换,又能为铜线键合工艺参数优化提供可靠的模型依据。
2.2 遗传算法优化
通过在训练完成后的BP神经网络中输出预测值,将此预测值编写成适应度函数,并在遗传算法中进行选择、交叉与变异,不断迭代优化,进而反向求解寻找到最佳适应度值 [16] 。本文采取在已有较优工艺参数组合的条件下,结合经验值,对工艺参数组合数值进行小范围调整,然后利用遗传算法进行迭代寻优。分别设定键合点1与键合点2的超声功率范围为32%~43%和36%~52%,键合压力范围为955~1 180 cN 和 1 030~1 285 cN,键合时间范围为135~155 ms和140~165 ms。
遗传算法进化迭代次数 N 为 500 次,种群规模 n=20,交换概率为0.4,变异概率为0.02。
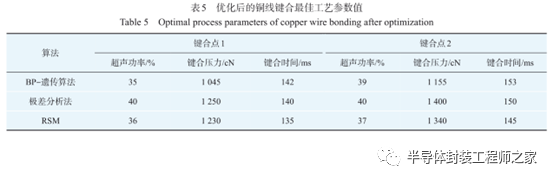
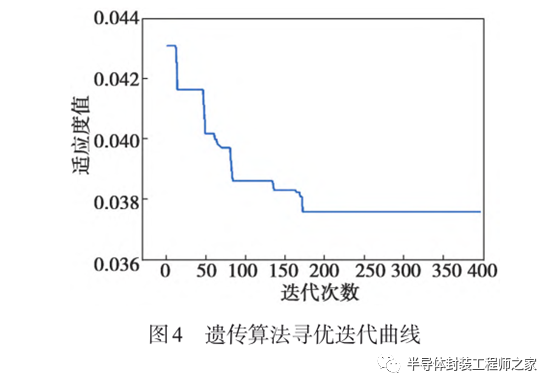
迭代开始时的适应度值最高,其值为0.043 1。随着迭代的进行,在算法进化至157次之后,适应度值达到最低,为0.037 6,如图4所示。对比遗传算法寻优前后的适应度值可发现,适应度值下降了14.6%,优化效果明显。适应度函数收敛处的最优个体平均值为最佳工艺参数。使用“BP‒遗传算法”与传统优化方法所得到的最优工艺参数值如表5所示。
3 优化验证分析
3.1 不同优化方法优化结果对比
采用不同优化方法得到的最佳工艺参数在AMB衬板上进行铜线键合试验,键合点2的键合效果图如图5所示。在保持剪切强度25 N的前提下,工艺参数优化前后键合点呈现出不同的键合效果:参数优化前,劈刀在键合点两侧产生了明显压痕,如图5(a)中的箭头标识所示,这是由于给定的工艺参数过大所导致的;而在参数优化后,只有极差分析法组的键合点两侧出现了明显的压痕。分析不同优化方法所得到的最佳工艺参数数值可知,虽然该组的超声功率数值与“BP‒遗传算法”组的相近,但其键合压力给定过大;而RSM组的键合压力数值偏大,不过其超声功率数值较小,从而导致了不同的键合效果。

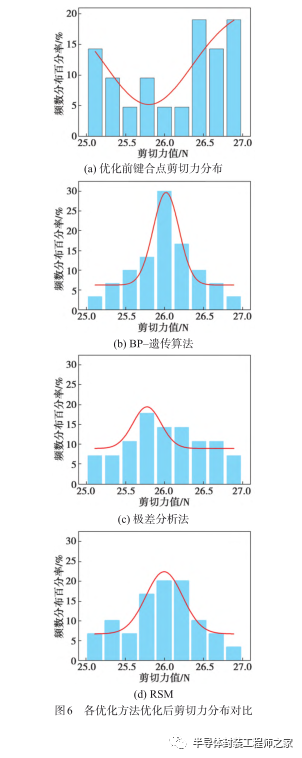
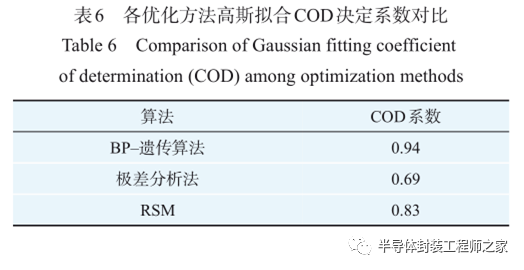
参数优化前后键合点的剪切力分布如图 6 所示。从图6(a)中可知,在工艺参数优化前,键合点剪切力分布不均匀,频数波动较大,影响了键合工艺的稳定性,不利于实际生产。对使用3种不同优化方法下的键合点剪切力分布进行高斯拟合,并进行决定系数(Coefficient Of Determination,COD)比较,COD值越大,表明高斯拟合优度越高,结果如表 6所示,“BP‒遗传算法”组的COD值最大,相比于传统的极差分析法与RSM分别提升了36.2%与 13.3%,表明其键合点剪切力分布最趋近于正态分布,键合工艺的稳定性更高。
3.2 功率模块试制与功率循环试验
当功率模块工作时,键合点1与DTS铜箔端直接接触,其承受的温度应力变化相比于键合点2更大。为评估工艺参数优化对整模块可靠性的影响,选取“BP‒遗传算法”组参数与2个试验组进行功率模块试制与功率循环试验,其中2个试验组工艺参数为仅在“BP‒遗传算法”组的基础上对键合点1的超声功率做梯度变化。图7为试制的1 200 V SiC 汽车级功率模块,芯片背面互连采用银烧结工艺,芯片正面采用DTS工艺进行铜线键合。

图8为在不同超声功率下3组试制模块与1组直径0.304 mm (12 mils) 铝线试制模块的功率循环能力对比图。铝线试制模块中的芯片与衬板互连采用的是传统钎焊工艺,同时由于铝线本身材料属性,因此其功率循环次数最少。
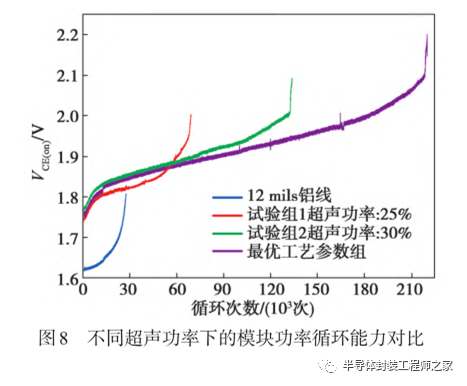
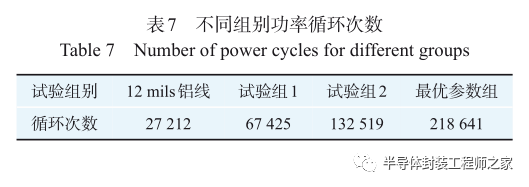
表7为各试制模块的具体功率循环次数结果。由表7可知,随着键合参数的优化,试制模块的功率循环寿命也显著提高;在3组模块的失效模式中,试验组1表现为部分键合点1翘起,这是由于低超声功率的键合点1其底部与衬底的互连层无法承受频繁的切应力变化所导致的;试验组2表现为少数键合点1松动;而最优工艺参数组的失效模式为AMB衬板与散热器基板之间出现了大规模空洞,但这并不是铜线键合工艺所导致的。
4 结论
本文在正交试验的基础上,结合BP神经网络与遗传算法提出了一种新的功率模块铜线键合工艺参数优化策略,以提高铜线的超声键合性能。在工艺参数优化设计中,首先采用极差分析法系统分析了工艺参数对键合点剪切力的影响权重,然后使用BP神经网络建立了对铜线键合点剪切力的预测模型,最后采用遗传算法对键合性能的适应度函数进行求解,从而获得最优工艺参数值。将“BP‒遗传算法”与传统优化方法的优化结果进行对比,经“BP‒遗传算法”优化后的工艺参数更能提高键合工艺的稳定性;在功率循环试验中,发现随着超声功率比的不断优化,功率模块的功率循环能力得到了显著提升。
来源:半导体材料与工艺
审核编辑:汤梓红
-
半导体引线键合清洗工艺方案2010-04-22 0
-
成本更低但键合性能相当甚至更好的铜线来代替金线键合2023-02-13 3067
-
有偿求助本科毕业设计指导|引线键合|封装工艺2024-03-10 0
-
新型铜线键合技术2009-03-07 525
-
大功率IGBT模块封装中的超声引线键合技术2011-10-26 1702
-
半导体集成威廉希尔官方网站 铜线键合性能有哪些?2023-02-07 1976
-
极小焊盘的金丝键合方案2023-02-07 5090
-
集成威廉希尔官方网站 铜线键合工艺技术详解2023-03-08 819
-
微波组件细间距金丝键合工艺的可靠性分析2023-05-16 1963
-
铜线键合设备焊接一致性探索2023-10-31 744
-
IGBT模块银烧结工艺引线键合工艺研究2023-12-20 1802
-
优化关键工艺参数提升功率器件引线键合的可靠性2023-12-25 1135
-
功率模块铜线键合工艺参数优化设计2024-01-02 510
-
预镀框架铜线键合的腐蚀失效分析与可靠性2024-11-01 1309
-
模块封装的关键工艺2024-12-04 201
全部0条评论

快来发表一下你的评论吧 !

