短时傅里叶变换STFT原理详解

传统傅里叶变换的分析方法大家已经非常熟悉了，特别是快速傅里叶变换(FFT)的高效实现给数字信号处理技术的实时应用创造了条件，从而加速了数字信号处理技术的发展。

大家对线性调频信号的波形和频谱非常熟悉，下面用Matlab仿真一个简单的线性调频信号，参数设置如下：

采样率：1000MHz

中心频率：300MHz

信号时宽：10us

信号带宽：100MHz

波形和频谱如下：

傅里叶变换是一种线性处理方法，不是看时域波形就是在频域查看信号频率，我们难以弄清信号的频率成分随时间是如何变化的。也就是从时域波形中看不出详细的频率特性，而从频谱图中也不知道具体的频率是在哪个时间段。

鉴于传统傅里叶变换的缺陷提出了联合时频的分析方法，既反映信号的频率，也能看出频率随时间变化的规律。而今天给大家介绍的就是线性联合时频分析方法中的短时傅里叶变换：STFT

STFT的基本思想是将信号加窗，然后再进行傅里叶变换，窗函数根据时间的变化在整个时间轴上平移，也就是利用窗函数将时刻t附近的频谱实现局域化，从而构成待分析信号的二维时频谱。

这样的话，即使信号是非平稳的或者是时变的，也可以假定被窗函数分割的每一个小段信号时平稳的，这样可以用STFT来分析信号的时频谱了，示意框图如下：

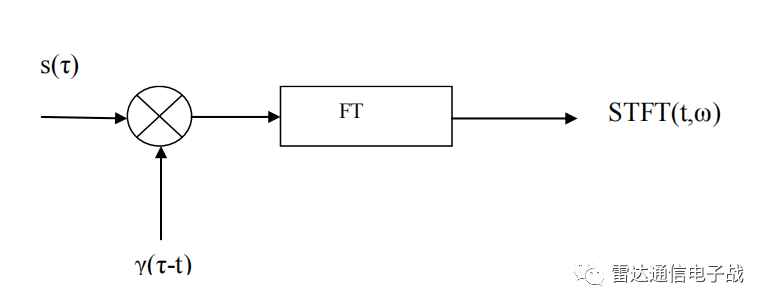
STFT是一个二维的复函数，表示信号随时间和频率变化的幅度和相位。离散傅里叶变换的表达式：

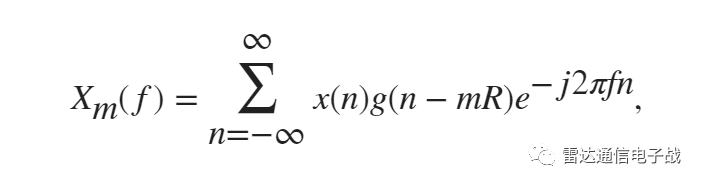
其中，g(n)是长度为M的窗函数；Xm(f)是mR时刻加窗后数据的DFT；R是每次DFT所跳的大小，它等于窗的大小减去重叠的长度L：R=M-L

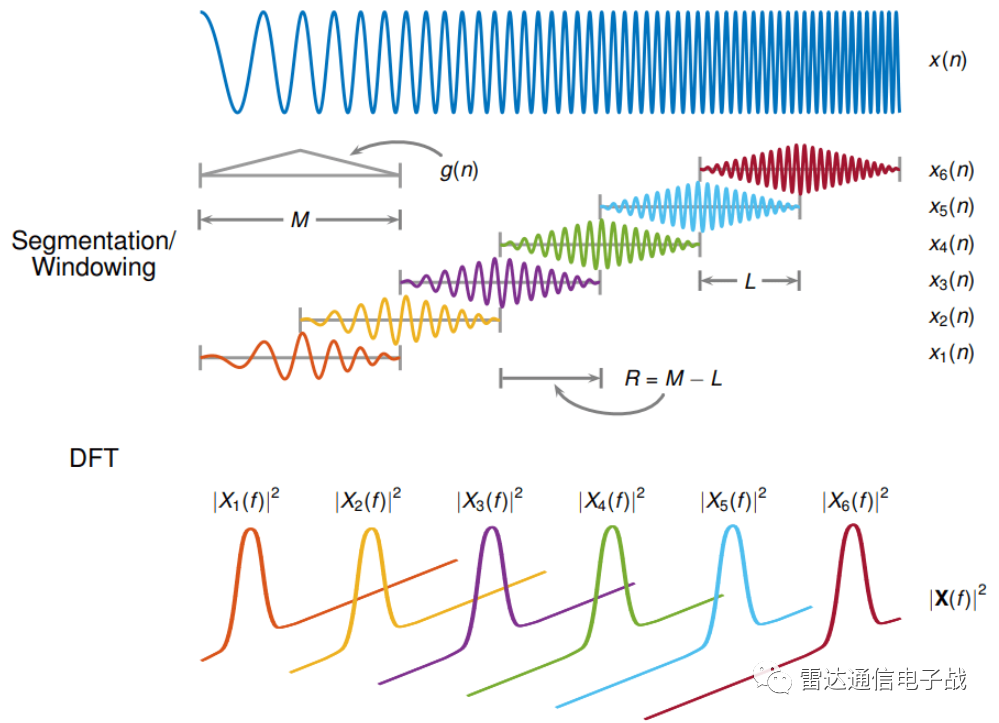
从上面的变换可以看出，通过不断移动窗函数的中心位置，得到不同时刻附近的傅里叶变换，这些傅里叶变换的集合就是STFT结果。

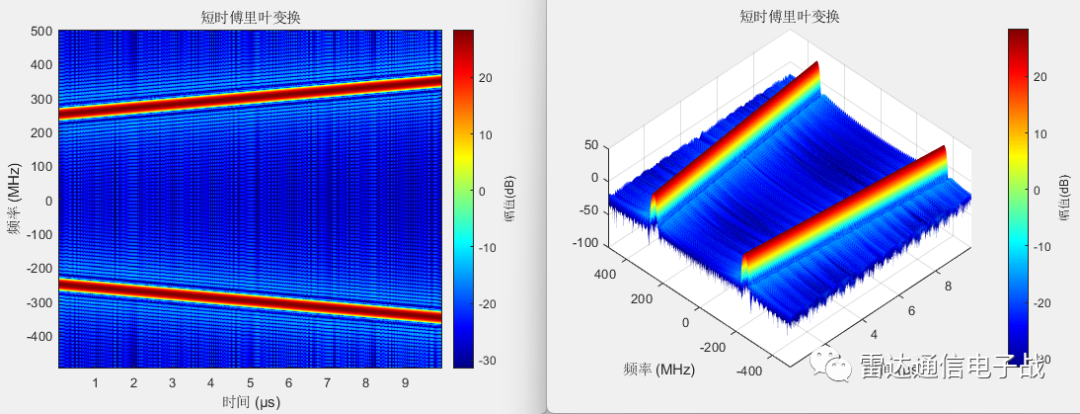
上图是上面线性调频信号的短时傅里叶变换结果，左图横轴是时间，纵轴是频率，颜色反映了值得大小。右图调整了观察角度。

审核编辑：汤梓红