一种基于扩散模型的傅里叶单像素成像高分辨率迭代重建方法

傅里叶单像素成像（FSPI）是一种基于傅里叶分析理论的计算光学成像技术。与传统基于阵列探测器的成像方法相比，FSPI在极弱光、大气湍流和散射介质等条件下表现出更高的探测效率和灵敏度。已在太赫兹成像、红外成像、光谱成像等领域展现出巨大的应用潜力。然而，FSPI一直面临着成像效率和成像质量的权衡问题。为实现高分辨率成像，需要较多的测量次数，这导致成像效率的下降。如何在不降低成像质量的情况下减少采样次数是目前面临的一大挑战。

为解决该问题，来自南昌大学成像与视觉表示实验室的研究团队提出了一种基于扩散模型的傅里叶单像素成像高分辨率迭代重建方法。该成果以“High-resolution iterative reconstruction at extremely low sampling rate for Fourier single-pixel imaging via diffusion model”为题发表在Optics Express。南昌大学副教授宋贤林，硕士生刘轩，本科生罗周旭为文章共同第一作者，刘且根教授为通讯作者。

主要研究内容

基于扩散模型的迭代重建策略包含低频傅里叶频谱采集和基于扩散模型迭代重建两个主要部分，如图1所示。基于分数的扩散模型被用于学习数据分布的先验信息。利用傅里叶单像素成像系统获取的真实低频傅里叶频谱被作为一致性项，与学习到的先验信息一起约束模型的迭代生成，实现在极低采样率下的高分辨率重建。

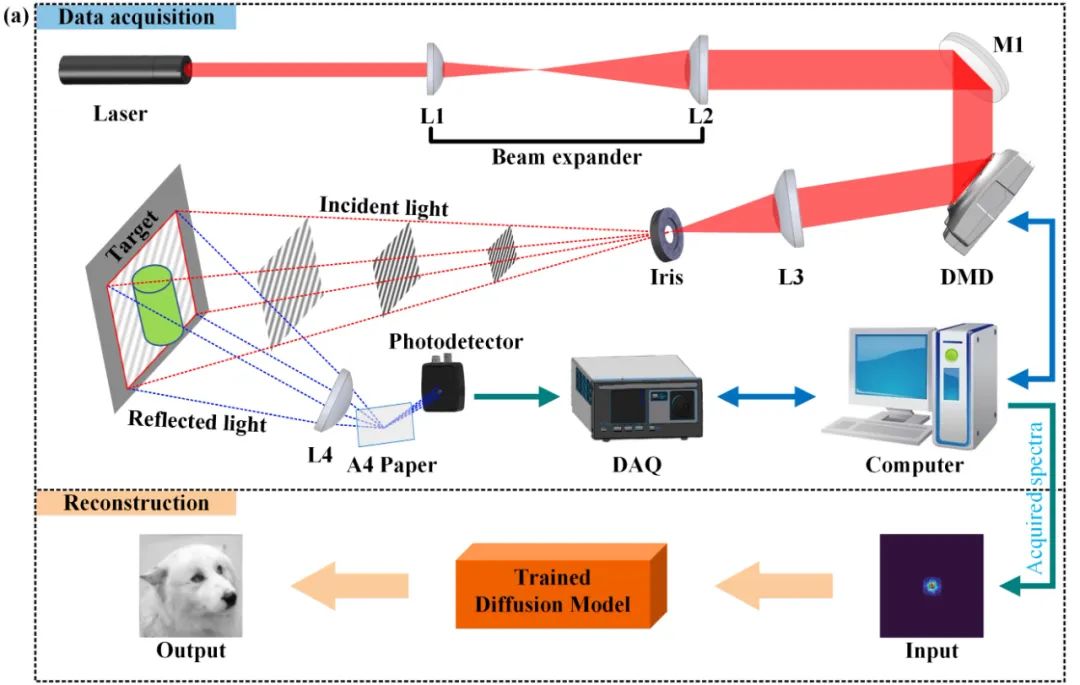
图1 系统总体方案

该方法流程如图2所示。训练阶段，对大量高分辨图像进行数据增强，获取丰富的数据样本。模型对样本不断添加高斯噪声来扰动数据分布，从而获取训练样本的内部统计分布。在迭代重建阶段，使用预测-矫正（PC）器作为逆向随机微分方程的数值求解器，并与一致性项（DC）相结合，进行条件生成。具体的，将随机噪声作为初始输入，利用逆向随机微分方程从学习到的先验分布中生成高分辨图像。在每一次迭代中，将实际采集的低频频谱作为数据一致项，并替换预测-矫正器输入图像的低频部分以实现条件生成。

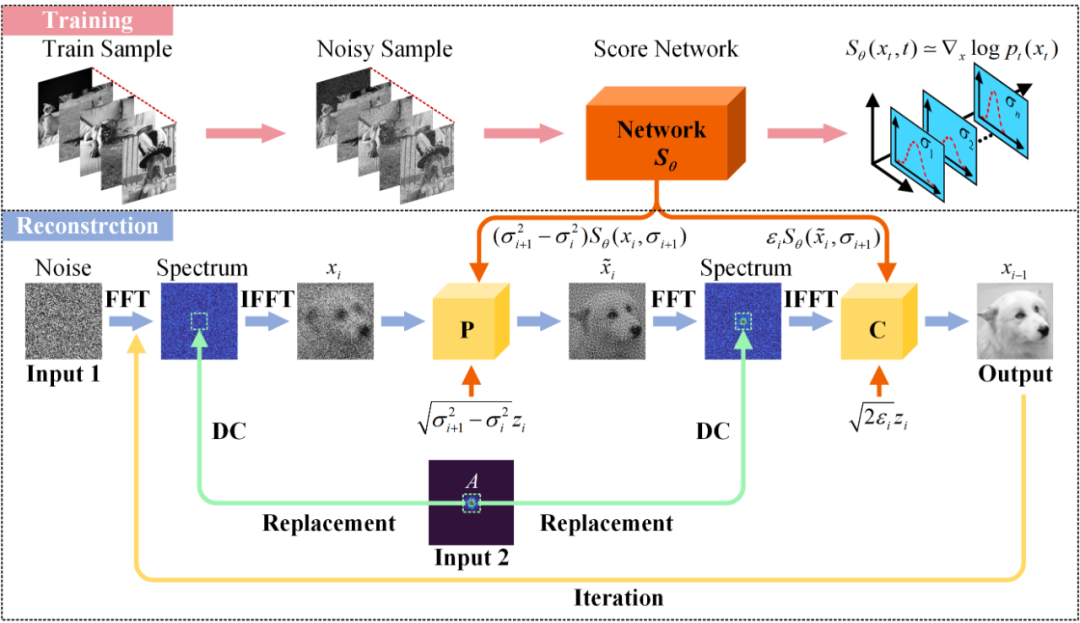
图2 基于扩散模型的高分辨率迭代重建流程图

研究团队进行了一系列极低采样下的仿真验证实验，并与主流的重建算法进行对比。相较于其他方法，该方法所得重建结果更接近真值图，具有更丰富的信息（图3）。在1% 极低采样率下， 所提方法表现出更卓越的性能， SSIM和PSNR分别提高了0.24和6.98 dB。

图3 动物仿真重建结果图以及对应的真值图和傅里叶频谱

在实际实验中，该方法依然具有良好的表现（图4）。在其他重建方法仅能看到硬币轮廓的情况下，所提方法能够清晰地看到硬币中的文字以及花纹。图像质量得分达到传统方法的3倍以上（图5）。以上结果均表明，所提方法即使在极低采样率条件下，依然能够获得高分辨的重建结果。

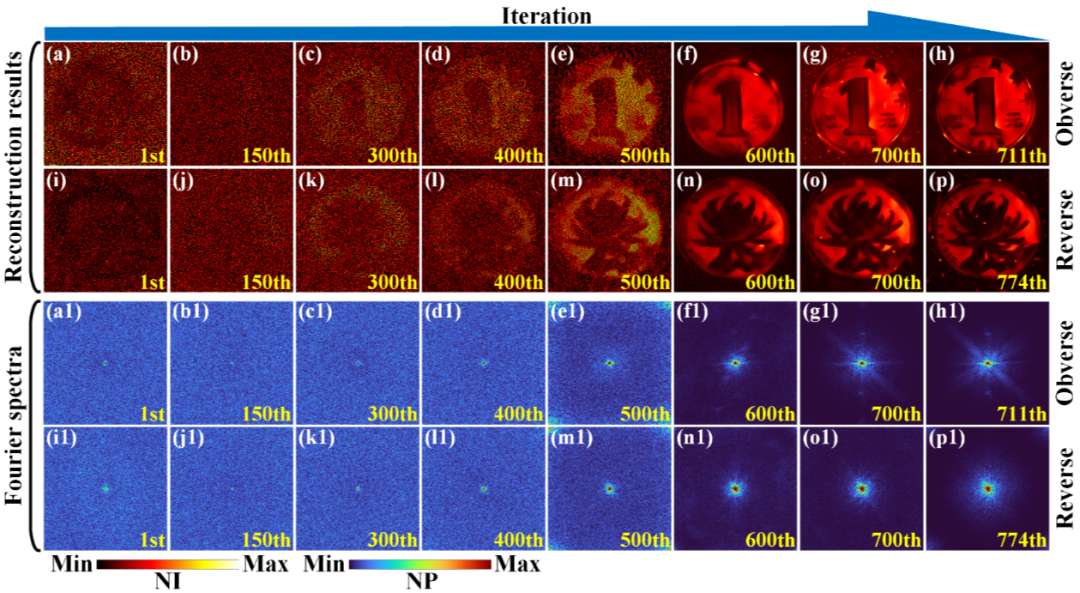
图4 硬币实际重建迭代过程

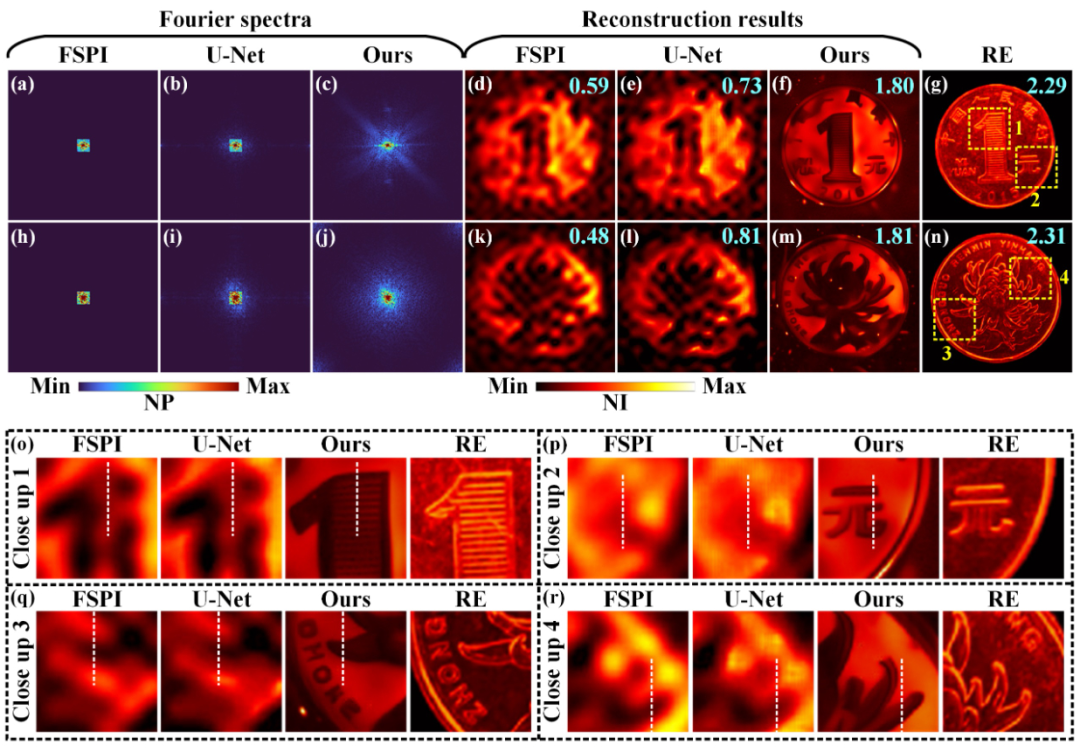
 图5 硬币实际重建实验

结论

本研究提出了一种基于扩散生成模型的新型FSPI重建方法，以解决在低采样率下FSPI重建质量低的问题。扩散模型被用于学习数据分布的先验信息，真实采样的低频傅里叶频谱被作为一致性项，与学习到的先验信息一起约束模型的迭代生成，实现在极低采样率下的高分辨率重建。仿真和实验结果表明，与U-Net方法和传统FSPI方法相比，所提方法在低采样率下具有显著的重建优势。在极低的采样率下（1%），优势更加明显。所提方法有望在不牺牲成像速度的同时实现高分辨率成像，从而进一步扩展FSPI在实际场景中的应用范围。

审核编辑：刘清