如何检测光学系统的纵向色差

摘要：现有的焦距检测方法通常由于检测仪器光源波长与光学系统不完全匹配从而产生纵向色差影响检测结果。针对这一问题，研究光学系统纵向色差的变化规律，并确定在400nm～1000nm波段用于表示其函数关系的Conrady 公式和复消色差特性公式。根据光学系统近焦位置的离焦量与位置呈线性关系的特性, 提出使用菲索干涉仪测量 5 种不同波长的焦距位置，获得单透镜和 双胶合镜头的纵向色差曲线。实验结果表明: 在400nm～1000nm波段单色系统和消色差系统的 纵向色差的函数关系分别符合Conrady公式和复消色差特性公式，研究结果为焦距的理论计算和精确检测提供了新的思路和参考。  

引言

在高精度成像中，对给定光学系统的焦距进行 测量是非常重要的。通常意义上的焦距是指某一 特定波长（一般为设计波长）的焦距数值，目前主 流的焦距检测设备的光源波长无法与被测光学系 统完全匹配，纵向色差会对焦距的测量结果产生 影响。纵向色差是描述光学系统在不同波长下 如何沿不同纵向位置聚焦，也称位置色差或轴向 色差。光学系统的性能经常受色差限制而非单色 像差限制，因此大多数成像镜头设计的目标都是 让所有波长尽可能聚焦在同一平面 ，在设计波 段范围内所有波长聚焦位置越接近这个相同平 面，在图像中观察到的问题就越少。纵向色差可 以通过测量光学系统在不同波长下的焦点位移来 评估，在一些简单的纵向色差检测实验中，对焦点 位置的确定是影响测量结果的一个重要因素。

为了准确检测光学系统的纵向色差，Seong等人提出一种利用马赫泽德干涉仪测量纵向色差的方法， 首先测量单透镜和双胶合镜头在多个波长下的透 射波前，然后利用波前Zernike系数确定各波长的 焦点位置，再使用 Sellmeir 公式计算400nm～700nm波段的色差曲线 ，进而得到被测系统的纵向色 差。这种方法在测量前需要对被测系统进行建模，从结果上看该方法对单透镜的色差曲线影响 误差较小，而对双胶合镜头的色差曲线影响误差 较大。本文针对这一问题，重点分析了不同类别 光学系统的纵向色差变化规律，并尝试使用Conrady公式和复消色差特性公式表示其函数关系，同时 提出一种基于菲索干涉仪测量光学系统焦点位置 进而获得光学系统纵向色差函数曲线的方法。  

1 原理

传统透射系统主要分为单色系统、消色差系统和复消色差系统。单色系统通常只工作在单一波长或极窄的波段范围内，大部分情况下使用同一种材料设计。由于折射率是波长的函数，光学系统的焦距也随着波长变化，所以单色系统的纵向色差是一条单调曲线。消色差系统为了消除色差，采用多种玻璃进行设计，由色差校正原理可知，对于大部分消色差系统来说，只能使2个波长聚焦在同一位置，且由于大部分消色差系统（如照相物镜）都是对“F、d、C”光进行校正，所以它们的色焦移曲线具有类似的形状。复消色差系统可以使3个波长同时聚焦在同一位置，其他波长情况下聚焦到这一平面的距离（即离焦量）相比消色差系统小很多，所以复消色差系统的像质远好于消色差系统，利用离焦量大小可以分析光学系统是否有效校正了色差，也可判断它们属于消色差系统还是复消色差系统。

不论是单色系统、消色差系统还是复消色差系统，它们的纵向色差都能用Zemax中的色焦移曲线（chromaticfocalshift）表示，色焦移曲线可用于确定光学系统纵向色差的函数关系。为了验证得到的函数关系是否符合实际，使用菲索干涉仪测量光学系统不同波长的焦点位置进行验证，将采集的离散数据代入纵向色差的函数表达式求解，评估函数曲线与实际测量焦点位置数据的一致性。

对于实际光学系统而言，衍射和像差的存在会对准确确定焦点位置造成一定困扰。在光学检测中，Zernike多项式Z3的物理意义是离焦，若测量的透射波前Z3为零，则表示该位置为光学系统的焦点位置。在零离焦位置，一些微小的机械调整误差会对Z3的数值产生明显的影响，导致无法准确记录焦点位置。在离焦量较大的位置微小调整X和Y倾斜对Z3的影响则可以忽略不计。鉴于Zernike系数Z3与位置呈线性关系已通过仿真和分析得到验证，本文通过测量离焦位置波前Zernike系数Z3计算被测系统的焦点位置，原理如图1所示。通过旋转测微旋钮推动导轨上五维支架使反射球面镜沿Z轴方向移动，测量被测光学系统在焦点附近若干个离焦位置的透射波前，并记录对应位置的Z3值，将Z3与位置数据按线性方程进行拟合，再使用拟合曲线计算出Z3为零时的位置。使用相同的步骤测量并计算被测系统在其他多个波长下的焦点位置，就可以得到纵向色差。

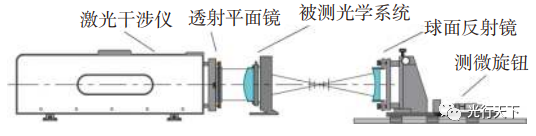
图1. 测量离焦位置的透射波前确定焦点位置原理

2 模拟仿真 2.1 单色系统

以一个单一材质的单色系统为例进行分析。具体参数为F数1.5，入瞳直径20mm，焦距30mm，波长范围400nm～1000nm，为方便数据采集分析选择400nm作为主波长。镜头结构图和色焦移曲线如图2所示。

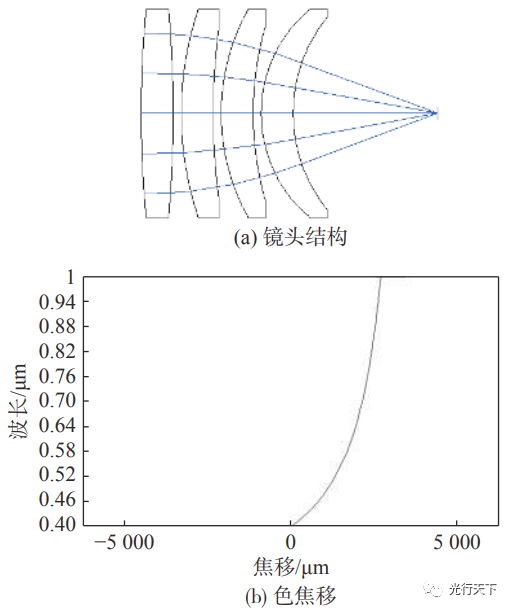
图2. 单色系统结构图与色焦移曲线 单色系统焦距随波长的变化主要由材料折射率引起，单调的 Zernike 系数-波长曲线可以使用Conrady 公式表示，与之相近单调的焦距-波长曲线也可使用 Conrady 公式表示成：

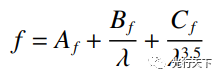
 （1） 式中：Af、 Bf、Cf分别为常数项系数和波长项系数。选取 530 nm、560 nm 和 720 nm 的焦距-波长数据代入（1）式求解系数：

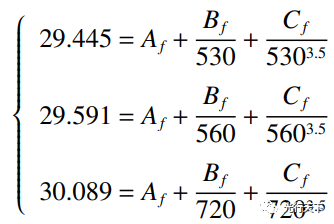
 （2） 计算后得到单色系统的焦距-波长曲线的函数 表达式为

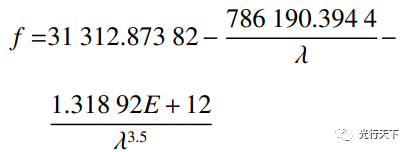
（3） 图 3（a）为单色系统焦距-波长仿真曲线与求解的Conrady公式曲线对比结果，图3（b）为曲线对比残差图。根据图3（b）显示，在400nm～1000nm波段内仿真和求解曲线焦距的最大绝对误差为23.11μm（λ=400nm），相对误差0.08%，求解曲线基本符合仿真曲线。由于单色系统的焦距-波长曲线均为类似的形状，因此Conrady公式可用于表示单色系统的纵向色差函数关系。

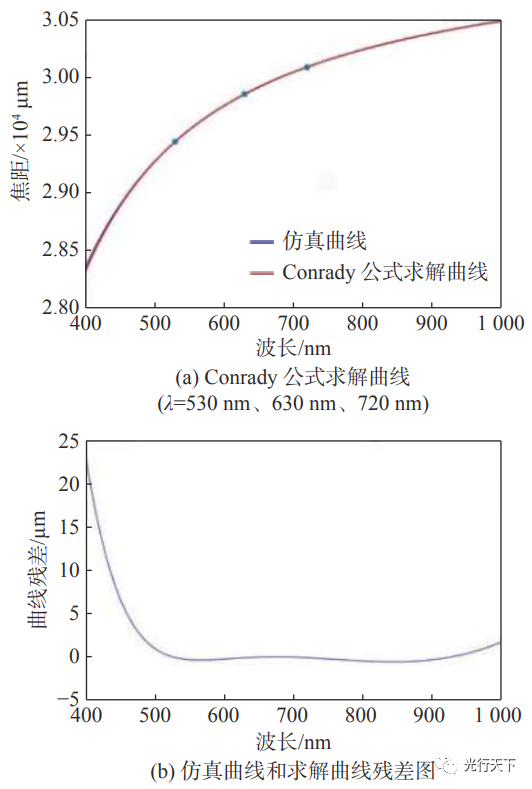
图3. 单色系统焦距-波长仿真曲线与Conrady公式求解曲线对比 2.2 消色差系统 以双高斯系统作为研究对象分析消色差系统的纵向色差。具体参数为F数2.5，焦距35mm，波长范围400nm～1000nm，主波长400nm，镜头结构图和色焦移曲线如图4所示。

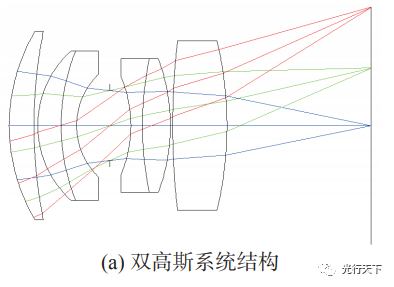
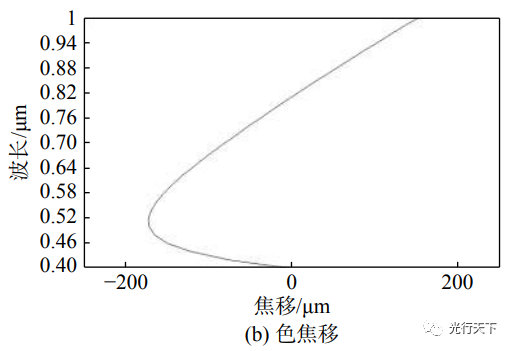
图4. 双高斯系统结构图与色焦移曲线图 消色差系统的色焦移曲线通常带有一个拐点，选取530nm，560nm和630nm的焦距-波长数据代入Conrady公式求解系数，得到双高斯系统的焦距-波长曲线的函数表达式：

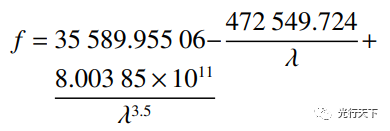
（4） 图5（a）为双高斯系统焦距-波长仿真曲线与Conrady公式求解曲线的对比结果。当波长范围较大时，Conrady公式求解曲线会出现较大偏差，图5（b）是仿真曲线与Conrady公式求解曲线的残差图。从图5可以看出，在波长1000nm处仿真曲线和Conrady公式求解曲线的最大绝对误差为47.47μm，相对误差为0.1349%。为了使求解曲线与理想曲线更吻合，尝试使用复消色差特性公式求解计算。复消色差特性公式是在Conrady公式基础上拓展一个波长项后得到的。

4 结论

焦距检测常会因为波长不匹配而引入色差，本文分析了光学系统纵向色差的变化规律，通过软件模拟和实验验证发现在400nm～1000nm波段，单色系统的纵向色差曲线可使用大家熟知的Conrady公式有效表示，而运用范围更广的消色差系统和复消色差系统的纵向色差曲线则需要使用复消色差特性公式表示，同时给出了复消色差特性公式幂级数系数范围的选定方法。本文还提出了一种基于菲索干涉仪测量光学系统纵向色差曲线的方法，通过测量离焦位置的透射波前Z3系数确定各波长的焦点位置，利用离散数据求解模型公式后获得400nm～1000nm波段内光学系统的纵向色差函数曲线。本文的研究工作表明，Conrady公式和复消色差特性公式除了适用于光学系统Zernike系数的变化规律外，还同样适用于光学系统的纵向色差，这对于焦距的精确测量具有指导意义。

审核编辑：黄飞