

数字滤波器对信号电平有什么影响?
EMC/EMI设计
描述
问题理解
使用数字滤波器时需要考虑的一个重要问题是信号电平对其数字到模拟域转换产生的影响。假设系统为处理单元提供数字信号,并在没有进行任何处理的情况下,使用一种理想的 DAC将其转换为模拟,如图1所示。本例中,我们将0-dBFS数字信号供给DAC,并把它转换成模拟域。满量程振幅信号编解码器规范中说明了数字编码和模拟输出振幅之间的关系。如果满量程振幅规范为0.707 VRMS(即1peak),这就意味着满量程0-dBFS数字正弦波将会产生1-Vpeak的正弦波,如图所示。
如果DAC的限制为–2n–1和2n–1–1,由于在输出端对其进行削波处理,因此对超出这些限制的信号进行放大处理会使信号失真(假设饱和逻辑),如图2所示。请注意,大多数信号处理器一般在向DAC提供数据以前都允许一定量的余量。处理器内存中的数据保持不失真很重要。图2描述了超出限制时可能会出现输出削波的一些DAC输入限制。
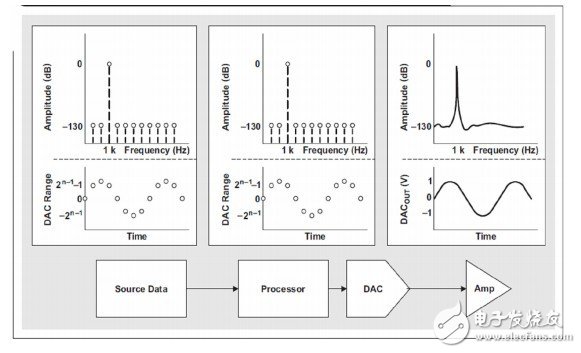
图1:表示为1-Vpeak模拟信号的满量程数字信号
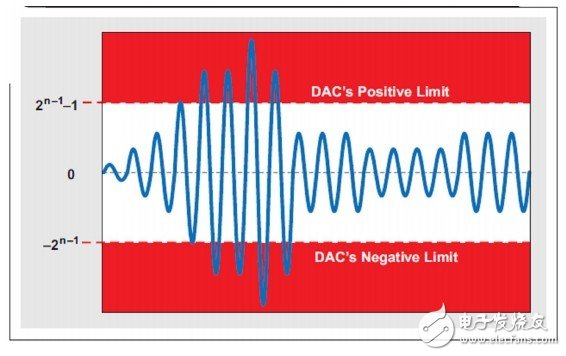
图2:数字域的过多增益可使信号超出DAC的上下限
这个问题的一种解决方案是保证放大信号时不超出DAC的限制(即保证不将正增益应用于源信号)。然而,许多情况下,这种解决方案的效果并不那么明显。在某个具体频率范围内,相对于满量程DAC输入振幅执行一次信号增强,也会带来一些不利影响。图3中,500-Hz信号增强6 dB。我们在模拟输出中观测到失真,这是由于DAC削波。
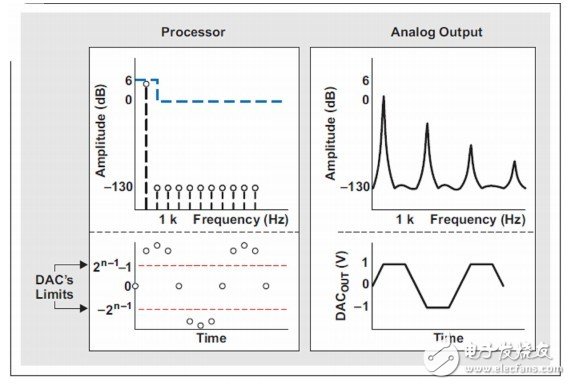
图3:指定频率带的可能升压效果
图4同样描述了这种概念。请注意,当传递到处理器内存的更大总线宽时,源数据的噪声得到了继承。如前所述,数据下调量为最大总信号增强量,以适应增强区域。但是,如图5 所示,即使增强参考点位于某个较好的位置,DAC信号也会受到输出SNR的影响。如果信号增强量并未极大地损害总系统SNR,则简单的调节或许是一种可行的解决方案。一些低功耗编解码器拥有100dB的SNR,其允许在不牺牲原始16位源SNR的情况下,进行一定量的调节。
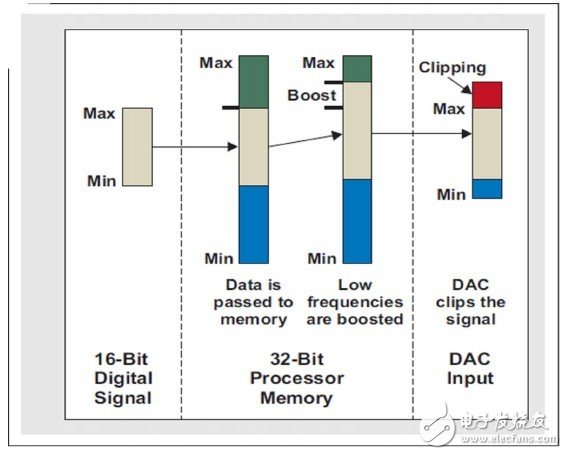
图4:全数字信号链的信号组成
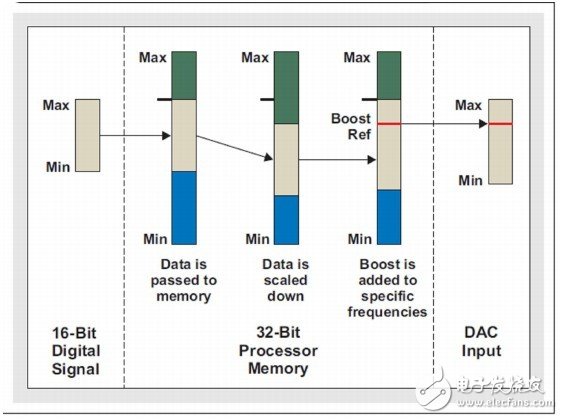
图5:使用调节时的信号组成
量化与数字表示法
在数字处理过程中,实数表示为一个具有固定精度的整数值。这被称作为量化法,而量化值是一个原始值的近似值。整数值可以表示为一个定点数或者浮点数。表示为定点数的某个整数值由数字位和小数位组成。表示为浮点数的某个整数值由指数位和尾数位组成。本讨论全部规定为定点数和定点运算。
在数字处理过程中,实数表示为一个具有固定精度的整数值。这被称作为量化法,而量化值是一个原始值的近似值。整数值可以表示为一个定点数或者浮点数。表示为定点数的某个整数值由数字位和小数位组成。表示为浮点数的某个整数值由指数位和尾数位组成。本讨论全部规定为定点数和定点运算。定点数表示为小数点(十进制小数点)后固定数位的二进制补码整数。这些数字组成数值的小数部分。小数点前面的数字为整数部分,并表示数值的范围。整数部分还包含数值的符号。
进入音频处理器的数字数据被认为是位于-1和1-1LSB之间的一个实数。假设实值表示为一个16位定点数, 则数值-1可以以二进制表示为1000000000000000(或者十六进制的 0x8000)。在二进制补码运算中,0x8000对应一个等于–32768的整数值。这就意味着,该整数值除以32768可以得到实值的量化近似值。二进制的16位最大正数为0111111111111111(或者十六进制的0x7FFF)。对应整数值为32767。将其除以32768换算系数,得到这种模式表示的最大实数。该数值为32767/32768 = 0.999969482421875。图6 显示了这种定点表示法。
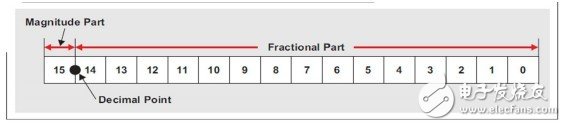
图6:实数的定点表示法
这种表示法中,共有15个小数位和1个整数位,同时也为符号位。这就意味着,量化以前实数必须位于-1和0.999969482421875之间。如果实数超过或者低于这一范围,其便无法以给定格式表示,因为 16 位寄存器会溢出。为了容纳更大的实数,我们需要增加整数部分,代价是减少小数部分。这种格式也被称作1.15格式(1=数字位,而15=符号位)。数字处理器的输入始终以 1.n 格式表示,其中n为小数位数(15、19、23或者31)。0dBFS值对应于满量程正弦波的RMS值,而该正弦波的幅值为 (2n–1)/2n。给定格式的最大实数以2n表示。用于表示某个信号的位数被称作信号位宽或者数据位宽。
溢出与饱和
处理单元计算产生值大于数据位宽值时出现溢出。溢出一般与累加器的计算有关,其相同符号的连续数值相加,然后存储起来。即使出现溢出以后,累加器一般还是会继续累加,因为只要不超出边界仍然还是会得到正确的最终结果。
在其被存储为信号值以前,累加器输出就已饱和。饱和是一个正溢出转换为最大正数而负溢出转换为最小负数的过程。饱和是一种非线性运算,并导致出现严重的输出谐波失真。我们使用余量位来防止饱和。
信号位
信号和噪声位影响系统性能。数字音频处理器增加量化噪声,整体性能是模拟威廉希尔官方网站 噪声和量化噪声的结果。假设两个噪声源都为独立随机过程的结果,则总系统噪声性能可定义为:
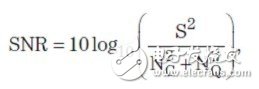
其中S为均匀分布的随机信号,NC为DAC威廉希尔官方网站 噪声,而NQ为量化噪声。使用100-dB DAC和120-dB信号处理器,会产生99.96 dB的总SNR。
我们应该注意到,总SNR也受到源—数字音频处理器输入的限制。如果输入为16位数,则系统的信号量化噪声比(SQNR)至多为96 dB(假设为均匀分布的随机信号,未加权)。因此,在这种情况下,就算是更高位的内部表示(更低的 NQ)也不会有明显的改善。
噪声位
如前所述,信号位数决定数字音频系统的性能。有时,滤波器响应计算会需要更多的位数。
滤波器实施包括一个信号流经并被存储为滤波器延迟元的数据通路。信号和延迟值乘以滤波器抽头相关系数。系数量化也对系统性能产生非常重要的作用。信号和系数值的积被存储在累加器中,其一般比信号具有更高的位宽。后续的积在累加器中相加(更高位宽),而最终滤波器输出再以信号精度存储(更低位宽)。
请思考图7所示双二阶滤波器实现。图中,输入和输出信号均以“A 位”表示。A和b系数以“B 位”表示。输入信号及其延迟元乘以系数,并在累加器相加。乘法器和累加器一共为 A+B位宽。之后,输出信号被Q模块量化,然后存储为一个A位数。这样便产生量化误差,其为数字滤波器的噪声源;因此,需要额外的位来确保数字滤波器的噪声影响低于目标SNR。这些额外位被称作噪声位。相比有限脉冲响应(FIR)滤波器,噪声对IIR滤波器的影响更加明显。噪声位数还取决于数字滤波器的采样频率和截止频率。随着采样频率上升,要求的噪声位数也增加。随着截止频率下降,要求噪声位数也随之增加。48-kHz工作时,14到16噪声位便足以维持40-Hz滤波器的目标SNR。

图7:双二阶滤波器实施
余量位
除了信号和噪声位,还需要更多的位来防止溢出。这些位被称作余量位。端到端音频处理链一般会保持信号电平。这就意味着,如果0-dB信号为信号链的输入,则输出为0dB或者更低。(一般会有一个能将信号摆动限制到零以下几分贝的信号压缩器。)如果我们使用升压滤波器来放大某些的信号频带,则其它频带一般会被衰减,以阻止信号升至0dB以上。就后一种情况而言,当输入信号电平为0dB时(也称作中性信号电平),输出信号会低于0dB,且仅放大后的频带会在输出端达到0dB。这样会降低音频信号的平均音量水平。
尽管信号电平维持在0dB,但在中间处理点信号还是会溢出。为了防止溢出,我们需要余量位—即除信号和噪声位以外的位。
共有两个溢出源:
1、音频处理链可以具有一个(在某些具体频率值)增益大于0dB 的滤波器。该滤波器可以为一个级联滤波器链(例如:低通、高通和/或带通滤波器等)的组成部分,其总增益为0dB,或者也可以是一个放大中性信号电平相关具体频率带的频率选择滤波器(例如:现成的EQ滤波器)。请注意,如果实数以1.n格式表示(其中n为小数位数),则数字的大小始终小于1。因此,如果使用一个0dB以上增益(大于1的实数)的滤波器,则输入值为 0dB(等于1的一个实数)时滤波器的输出值将会溢出。为了防止在这类情况下出现溢出,我们需要更多的余量位。
2、增益小于或者等于0dB的滤波器会有大于1的瞬态实值。为了确保这些瞬态值不溢出,需要使用余量位。
图8显示了音频处理器中信号的图示。需要注意的重要一点是,余量位主要用于适应中间信号增长。预计在最终处理模块的末端,输出将会恰好位于信号位宽内。另外,低信号振幅时,输出仍然会在限制以内,而不会失真;但是,高信号振幅时,输出将会饱和,并引起失真。为了防止出现失真,最好是在最终输出以前让信号衰减。
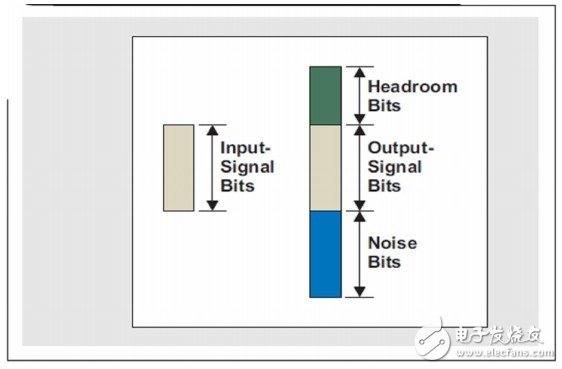
图8:余量位信号表示法
调节
调节用于避免增益超出0dB的滤波器出现饱和。我们可以专门使用一个升压滤波器,获得某个特定频率。即使是一个多节低通滤波器也会有一个双二阶节,其实际获得某些高于有效余量的频率(总响应仍然为0dB)。在这种情况下,使用还是不使用调节方法,取决于输入信号电平乘以总滤波器响应的最大增益。如果乘积大于有效DAC余量,则可以使用调节方法来避免饱和。
一种调节方法是让系统的传输函数衰减一定量,该量的大小等于滤波器传输函数的最大振幅。调节因数可以定义为:

其中0≤ω ≤ π。第二种方法是将输入信号做S调节。图9展示了调节传输函数的效果。满量程正弦波为传输函数的输入,其让平坦频率衰减6dB。相对于–6dBFS,1-kHz 信号增强了6 dB。
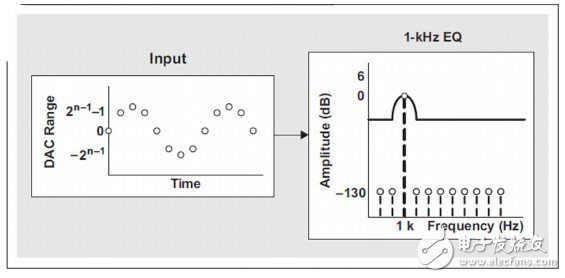
图9:传输函数调节
在一些情况下,由于滤波器结构和瞬态信号序列,滤波器的输出会高于0dB,尽管其并没有0dB以上的增益。如果单个内存单元为0dB,且符号与抽头相反,则FIR滤波器可以使信号增益增加的量为滤波器抽头绝对值的和。滤波器响应不能超出0dB,因此要使用额外余量。IIR滤波器额外余量的计算较为复杂,因为它们有许多反馈单元,同时要找到决定瞬态增益上限的闭型表达式是一个复杂的过程。实际上,信号处理器提供额外余量(DAC 限制以上)的原因之一是允许瞬态值余量。我们可能会需要进行一些测量,来计算额外余量。某些情况下,可能需要对SNR做一些让步,以处理饱和带来的失真问题,同时还可能会需要增加模拟增益来让信号归于0dB。
使用调节方法,有时需要在模拟输出级中添加额外增益(升压)来进行补偿。应特别注意的是,要确保升压区域的信号不会使输出放大器饱和,因为它会导致出现失真信号。在处理器的最终输出级同样也有升压,目的是对信号调节进行补偿。这是一些多节、0dB滤波器所要求的,其信号调节的目的是防止一个或多个单节出现溢出。就那些获得0dB以上频率的滤波器(现成的EQ滤波器)来说,中性信号电平被调节至0dB以下。这种情况下,并不要求末级升压。结果是损失了平坦区域的SNR。
一种更讲究的解决方案是根据数字处理器应用的音量增益来限制滤波器增益的大小,其非常适合于耳机应用。在高音量时,降低频率升压并最终在全音量时为平坦。
在一些情况下,频率升压保持恒定,而在高音量时对信号进行压缩。这便是抗削波动态范围压缩器 (DRC) 功能:低音量时,保持原始SNR;但随着音量的增加,调节度也成比例增加来防止出现失真。
不管使用哪种方法,充分考虑人们对声音和噪声的感知过程都是很重要的。人的听觉有一个明显的动态范围。耳机放大器在噪声层和输出功率之间进行平衡,以最好地适应这一范围。例如,TLV320AIC3254音频编解码器能够向典型32-Ω或者16-Ω耳机负载提供非常高的纯 500 mVRMS 声压级 (SPL),同时具有满量程以下100dB的噪声底限(加权值),其在人的听觉阈值以下(请参见图 10)。有时,甚至没有必要在实施调节以后增加额外的放大率,因为输出功率远高于舒适听觉水平。
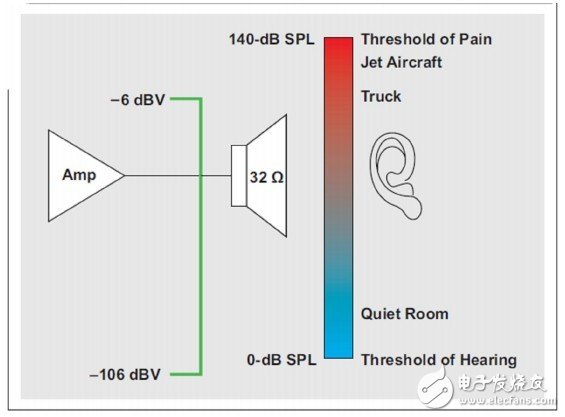
图10:相对人类听觉的耳机音量
-
如何设计数字滤波器?2019-10-11 0
-
数字滤波器的设计与应用2008-08-26 1127
-
数字滤波器(DF)的基本结构2008-12-07 676
-
数字滤波器的结构2009-01-07 721
-
数字滤波器的原理及其设计2009-11-24 925
-
用FPGA设计的四阶IIR数字滤波器2008-01-16 1433
-
数字滤波器的设计实验2008-10-30 5802
-
什么是数字滤波器2009-06-30 3998
-
数字滤波器,数字滤波器原理是什么?2010-03-24 28678
-
IIR数字滤波器设计2015-12-25 912
-
基于matlab的数字滤波器的设计及数字滤波器基本结构2018-06-05 1716
-
FIR数字滤波器设计2022-04-05 5699
-
数字滤波器是什么 数字滤波器的性能指标2023-02-24 5669
-
数字滤波器和模拟滤波器有哪些区别2023-06-27 1374
全部0条评论

快来发表一下你的评论吧 !

