一种新型机翼应变载荷关系神经网络模型

摘要

建立飞机结构应变载荷关系模型时，地面标定试验数据保真度高、但工况范围及数量受限，有限元仿真工况范围覆盖广、但数据保真度低，导致单独依据地面标定试验数据和有限元仿真数据建立的应变载荷关系模型难以兼顾适用范围和预测精度。对此，本文提出了映射式与补偿式两种融合“试验-仿真”虚实数据的多级神经网络架构，开发了基于子学习器方差的模型认知程度度量方法，形成了精度高、适用性广、能够预警不可靠输出结果的机翼应变载荷关系神经网络模型，并采用缩比机翼对上述模型进行了验证。本研究表明：虚实数据融合的神经网络模型能够更好地描述机翼的应变载荷关系，且补偿式模型的预测效果优于映射式模型；本文提出的模型认知程度度量方法，能够在不影响模型预测精度的前提下，有效判别出神经网络模型认知程度差的数据样本，对神经网络的不可靠输出做出预警。

关键词

应变载荷关系；飞机结构；数据融合；神经网络模型；子学习器

飞行实测是获取飞机结构实际服役载荷历程的最可靠途径，对于飞机的定寿、延寿具有重要意义[1]。目前，获得实测飞行载荷的主要方法是应变测量法[2]，即：通过地面标定试验，基于飞机结构真实响应，得到若干“载荷-应变”数据样本，并建立应变载荷关系模型（传统上一般为多元线性回归方程组），并依据此模型和飞行实测应变推演飞行中的结构载荷[3-5]。可以看出，应变测量法的核心是获取能够充分反映飞机结构真实特性的应变载荷关系模型。然而，受试验周期与成本的限制，地面标定试验往往只能获得有限的弯剪扭复合工况的数据样本，导致应变载荷关系模型对复杂载荷下飞机结构特性的认识“不够广”[6]；受试验技术的限制，地面标定试验的载荷水平无法覆盖部分大机动、大过载飞行下的载荷水平，导致应变载荷关系模型对飞机结构实际特性的认识“不够深”。因此，仅基于地面标定试验样本数据建立的应变载荷关系模型，存在适用范围上的不足[8]。

针对上述问题，不少研究提出，可通过有限元仿真开展“虚拟标定试验”，从而在不显著增加成本的情况下，拓展对飞机结构特性认识的广度、深度[9]。杨全伟等[10]采用有限元方法模拟地面标定试验，在减少地面标定试验成本的同时获取到了更充分的标定数据。然而，单纯的虚拟标定试验的仿真结果与真实试验结果偏差大，依据试验实测信息修正有限元模型也无法完全消除这一偏差，导致基于“虚拟标定试验”建立的应变载荷关系模型的预测精度难以达到可接受的水平。例如：S.B.Cooper等[11]基于某飞机翼肋的实测应变数据，对翼肋的精细有限元模型进行了校准，但有限元仿真计算应变与实测应变的误差仍可达到约5%。孟敏等[12]基于材料性能、结构几何、应变计位置等相关参数，对某型飞机机翼的有限元模型进行了校准，提高了仿真模型的可信度，但载荷预测误差最高可达到13.3%。因此，仅基于“虚拟标定试验”样本数据建立的应变载荷关系模型，虽然解决了适用范围问题，但又引发了预测精度不足的问题。

近年来，机器学习等技术迅猛发展，已经能够从数据的表层关联中挖掘出背后的深层规律，建立高精度的映射关系描述模型[13-15]，并在此基础上，扬长避短各取所长，将保真度高的试验数据与覆盖工况范围广的有限元仿真数据有机地融合，建立保真度高且适用工况范围广的神经网络模型，能够在一定程度上应对兼顾精度和适用范围的映射关系描述问题[16,17]。但同时，相关研究也发现，对于神经网络等机器学习模型，如果输入样本与训练数据集偏离程度较大、甚至超出了神经网络的知识边界，神经网络模型就会输出“过度自信”的错误预测结果[18-21]，给后续工作带来隐患。因此，必须开展相应的方法研究，评估神经网络模型对样本的认知程度、甄别其不可靠的输出结果。

对此，本文针对机翼应变载荷关系的高精度、宽范围描述需求，基于“试验-仿真”融合的解决思路，提出了映射式与补偿式两种神经网络模型，建立了基于子学习器方差的模型认知程度度量方法，并在此基础上，发展出了精度高、适用性广、能够预警不可靠输出结果的机翼应变载荷关系神经网络模型，并依据缩比机翼对模型效果进行了验证。

01

机翼应变载荷关系的虚实融合神经网络模型

地面标定试验和有限元仿真获取的都是“测点应变-截面载荷”样本数据，但前者是少量的高保真度“实”数据，而后者是大量的低保真度“虚”数据。基于虚实数据融合的应变载荷关系神经网络模型应当包括预测模块和融合模块两个

部分，因此若按照两个模块之间的相互关系，则建立这一神经网络模型存在两条具体途径——

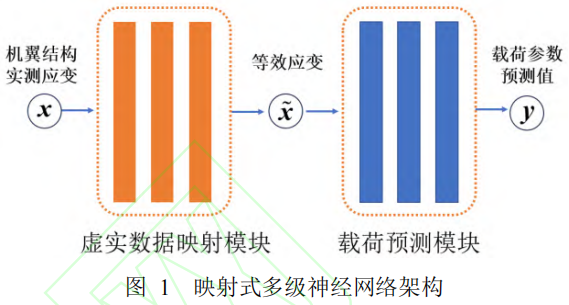
①先融合后预测。即，先将高保真度应变数据变换为低保真度应变数据空间中的等效应变，再将其输入到基于限元仿真低保真度数据所建立的载荷预测模块；此时，虚实数据融合的内涵实际上是将高保真度应变数据“映射”到低保真度应变数据空间中。

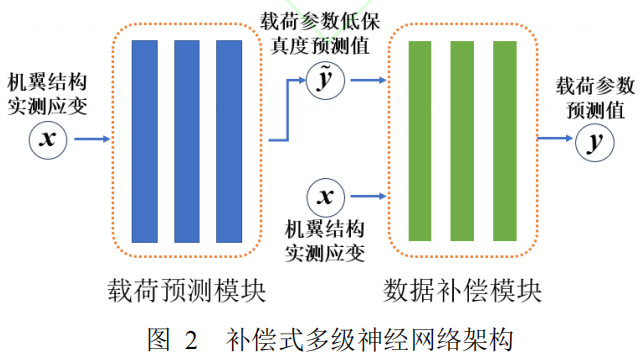
②先预测后融合。即，先由基于有限元仿真低保真度数据所建立的载荷预测模块给出预测值，再通过基于地面标定试验高保真度数据所训练出的数据融合模块对其进行校正；此时，虚实数据融合的内涵实际上是通过高保真度数据实现对低保真度载荷预测模块的“补偿”。

针对上述两条途径，本章首先对标定试验所获得的样本数据进行介绍，然后分别提出映射式和补偿式的多级神经网络架构，并建立相应的应变载荷关系模型。

 

 

 

 

 

02

基于缩比机翼的模型验证

本工作以某缩比机翼为对象，通过有限元仿真开展了虚拟标定试验、通过增材制造铝合金缩比机翼件开展了地面标定试验，分别建立了数据集，用于训练本文提出的映射式与补偿式两种虚实融合架构的神经网络模型。此外，本文还训练了仅使用虚拟标定试验数据的非融合神经网络、仅使用地面标定试验数据的非融合神经网络及同时使用两种数据的非融合神经网络，用于对比分析。

2.1缩比机翼虚实标定试验数据集

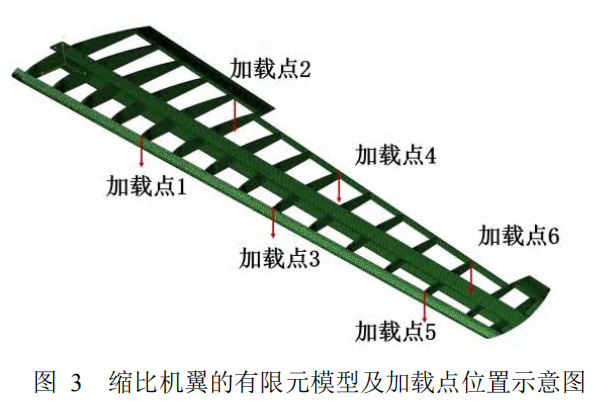
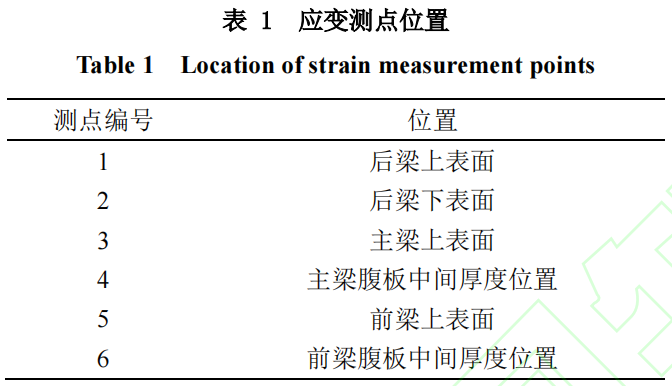
缩比机翼的翼展约35厘米，其有限元模型如图3所示。机翼共布置了6个加载点，分别位于5肋、9肋、13肋与前梁、后梁的交界处；在翼根处共布置了6个应变测点，其具体位置见表1。

 

2.2模型训练与结果分析

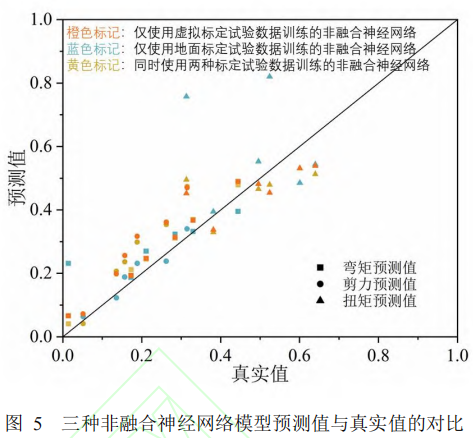
三种非融合神经网络对于地面标定试验数据集中各测试样本的预测结果如图5所示。可以看出，多数情况下，同时使用两种标定试验数据训练的非融合神经网络的预测值（黄色标记点）与仅使用虚拟标定试验数据训练的非融合神经网络的预测值（橙色标记点）都较为接近，这是由于虚拟标定试验的数据样本量远远多于地面标定试验，如果将这两种数据样本不加区分地同时用于神经网络训练，地面标定试验样本无法得到足够的重视，神经网络最终完全依赖于从虚拟标定试验样本中学习到的知识做出决策。同时可以发现，仅使用地面标定试验数据训练的非融合神经网络（蓝色标记点）对少数几个测试样本的预测值极大地偏离了真实值，这可能是由于测试样本与训练样本偏差较大，对此，本文将于第3节做出讨论；而对于除此以外的大多数样本，其预测效果都比其他两种非融合神经网络更好，说明其他两种非融合神经网络由于受到仿真误差的影响，预测表现不佳。因此本文选取仅使用地面标定试验数据训练的非融合神经网络作为与本文提出的补偿式、映射式神经网络模型分析对比的基准。

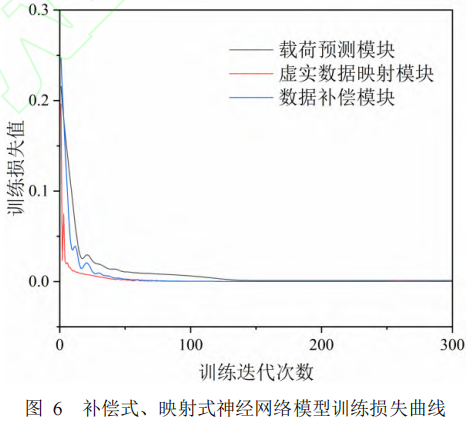
在训练过程中,映射式以及补偿式神经网络模型中各个模块的训练损失值如图6所示，可见训练过程中损失值收敛稳定，大约在迭代次数为300时即可得到图7结果。

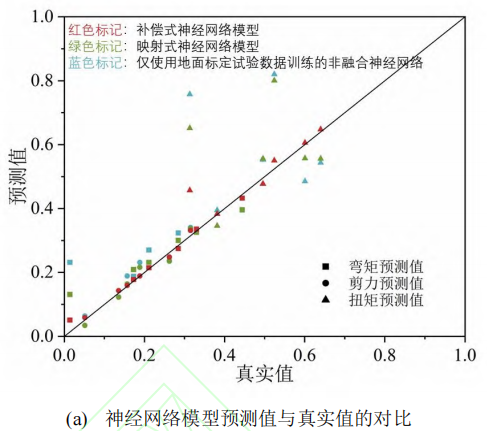
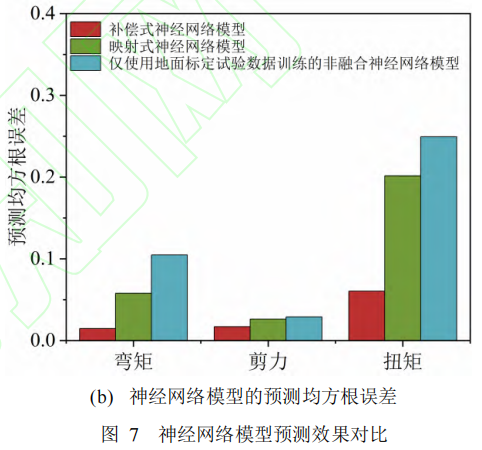
补偿式、映射式神经网络模型以及仅使用地面标定试验数据训练的非融合神经网络对于地面标定试验数据集中各测试样本的预测结果如图7所示，其中，图7(a)为三种神经网络模型的预测值与真实值的对比，图7(b)为三种神经网络模型的预测均方根误差对比。均方根误差的计算公式如下：

可以看出，相比于仅使用地面标定试验数据训练的非融合神经网络，补偿式、映射式神经网络模型的预测效果均有所提升，这说明融合来自虚拟标定实验与地面标定试验的两种试验数据，可以改善神经网络模型的预测效果。

在大多数测试样本中,尽管映射式神经网络模型的预测效果优于仅使用地面标定试验数据训练的非融合神经网络模型，但是其预测值与真实值的偏差仍然较大、且其预测均方根误差仅有较小程度的降低。这是因为在映射式神经网络模型中，虚实数据映射模块的输入信息过于单一，难以准确捕捉虚拟标定试验数据与地面标定试验数据之间的映射关系；因此，与仅使用地面标定试验数据训练的非融合神经网络模型相比，映射式神经网络模型的预测效果提升有限。

相比于映射式神经网络模型，补偿式神经网络模型的预测效果明显更优，在大多数测试样本中，其预测值与真实值仅有微小偏差；与仅使用地面标定试验数据训练的神经网络模型相比，补偿式神经网络模型的预测误差大幅降低，其中弯矩载荷的预测均方根误差降低了86.10%，剪力载荷的预测均方根误差降低了41.76%，扭矩载荷的预测均方根误差降低了75.75%。这是因为，补偿式神经网络模型的高保真度模块不仅能接受测点应变信息作为输入，同时还可以得到低保真度模块的载荷参数预测值，接受的信息更加全面，也就能够更加深入地挖掘出数据背后的深层规律。

综上所述，本文提出的“试验-仿真”标定数据融合方法可以有效提升神经网络模型的预测精度；且相比于映射式神经网络模型，采用补偿式多级神经网络架构的神经网络模型可以更好地实现虚实数据的融合利用，大幅降低对载荷参数的预测误差，初步解决了应变载荷关系模型对复杂载荷下飞机结构特性的认识“不够广”的问题。由于基于有限元仿真的虚拟标定试验无需考虑各个加载点的限制载荷，所以使用这种数据融合方法也有潜力将应变载荷关系模型的预测能力扩展到大机动、大过载飞行工况，从而解决其对飞机结构实际特性的认识“不够深”的问题。未来，还可以使用能够考虑时序信息的神经网络模型，将本方法的适用范围拓展到动载荷预测。

03

模型对样本认知程度的讨论

对大多数测试样本而言，补偿式虚实融合神经网络模型能够获得与真实值相对一致的预测结果，但仍有部分预测结果明显偏离了零误差线（如图7(a)中横坐标约为0.3、纵坐标约为0.47的红色三角形数据点——偏差超过45%），这说明神经网络模型在训练过程中没有学习到此类样本的有效信息，导致其对此样本的认知程度较差，给出的预测结果的准确度较低。

因此，在发展虚实数据融合的机翼应变载荷关系神经网络模型时，有必要同步考量模型对样本的认知程度，将模型训练时未能充分学习到的样本识别出来，从而对神经网络的不可靠预测结果做出有效预警。

3.1嵌入子学习器的应变载荷关系神经网络模型

由于不可能对各虚拟工况都开展地面标定试验而获得载荷实际值，实际工作中无法通过预测值与实际值的偏差来识别应变载荷关系神经网络模型对样本的认知程度，因此，考量模型对样本的认知程度，必须依据模型预测误差之外的其他参量。

不同神经网络模型（用相同训练集数据训练获得）对同样本预测结果的方差，是满足上述需求的一个参量，能够有效反映模型对样本识别程度和预测可靠性。原因在于：如果某一样本与神经网络模型的训练样本较为接近，神经网络模型在训练阶段已经充分地学习了这类样本，那么各神经网络模型会给出比较统一的预测，反映为各神经网络模型预测结果的方差就比较小；相反，如果某一样本与神经网络模型的训练样本偏差较大，神经网络模型在训练阶段就无法充分地学习这类样本，导致各个神经网络模型对这一样本的认知不统一，最终就会给出分歧程度较大的预测结果，反映为各神经网络模型预测结果的方差比较大。

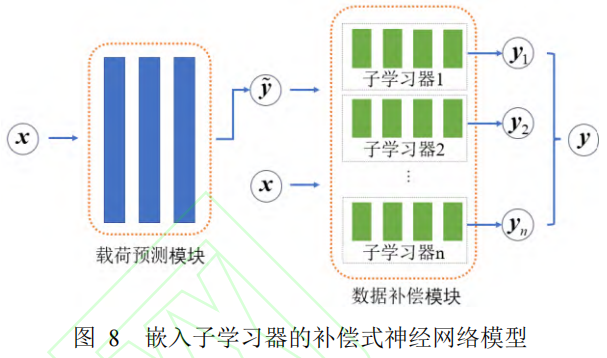
对此，本文提出了一种依据预测值方差的模型认知程度识别方法。该方法采用集成学习的思路，在补偿式神经网络模型中，嵌入若干个子学习器，从而人为地在虚实融合应变载荷关系神经网络模型中创造多个描述相同映射关系的神经网络子学习器，并通过计算各子学习器预测值的方差，来识别神经网络模型对样本的认知程度。嵌入子学习器的补偿式应变载荷关系神经网络模型如图8所示，模型中各子学习器除隐藏层神经元数量不同外，其余完全相同。

3.2子学习器方差法认知程度识别效果验证

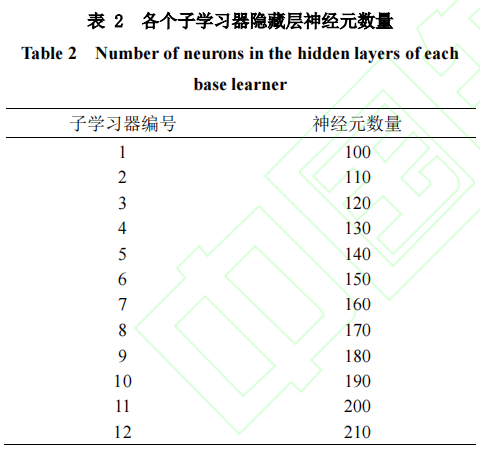
基于嵌入子学习器的补偿式神经网络模型，使用子学习器预测方差对上述各个测试样本进行神经网络模型认知程度的度量。以扭矩载荷为例，在补偿式神经网络模型的数据补偿模块中，嵌入总共12个子学习器，各个子学习器的隐藏层神经元数量见表2。

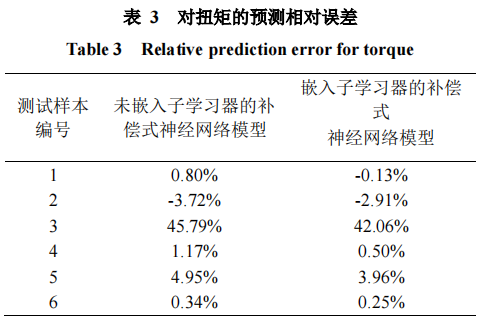
对于各个测试样本，按照式(14)计算其神经网络模型的预测值，见表3。可以看出，嵌入子学习器的神经网络模型对1、2、4、5、6号测试样本的认知程度较好，其相对预测误差都在5%以内；对3号测试样本的认知程度很差，其相对预测误差高达42.06%。该结果与未嵌入子学习器的神经网络模型是一致的。特别地，嵌入子学习器后，补偿式神经网络模型的预测相对误差不但没有上升、反而稍有降低，表明嵌入子学习器不但不会降低、反而能够小幅提升神经网络模型的预测能力。

进一步，按照式(15)计算各个测试样本的子学习器预测方差，如图9所示。对于1、2、4、5、6号测试样本，子学习器的预测方差都比较低，且大致处于同一数量级。特别地，对于编号为3的测试样本，子学习器的预测方差明显高于其他样本，即各个子学习器的预测分歧程度较大，说明神经网络模型在训练阶段未能充分学习到3号测试样本的相关知识，导致对3号测试样本的预测结果可信度较低。该结论与基于预测相对误差的判别结果是一致的；换言之，子学习器方差法成功地指出了相对预测误差最高的测试样本，即有能力甄别出神经网络模型认知程度较低的样本。

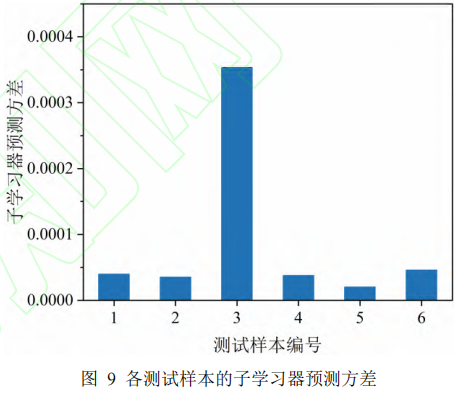
综上所述，基于嵌入子学习器的补偿式神经网络模型，采用子学习器的预测方差可以表征神经网络模型对样本的认知程度；使用子学习器方差法，可以正确识别神经网络模型认知程度差的样本，从而对神经网络模型的不可靠输出做出预警。

3.3子学习器数量对识别效果的影响

在对样本认知程度的识别过程中，判别效果可能会受到子学习器数量的影响：如果子学习器的数量太少，则计算出来的预测方差可能不具有代表性，导致误判的发生；但如果子学习器的数量过多，效果不会显著提升，还会增加训练时间的负担。对此，本节研究了子学习器数量对预测方差的影响。使用包含不同数量子学习器的神经网络模型，对各个测试样本进行认知程度辨识，计算其预测方差，绘制成图10所示的曲线。

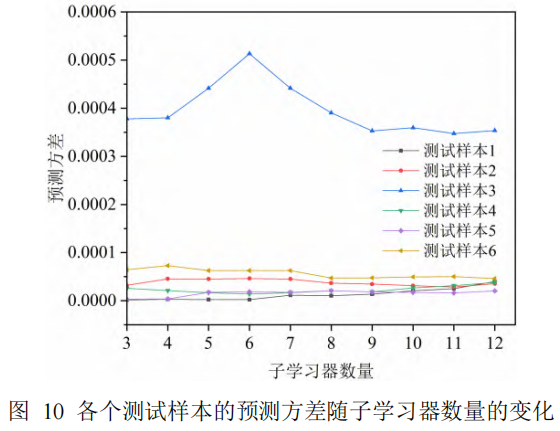
可以看出，随着子学习器数量的增加，除了测试样本3以外的测试样本的预测方差基本都较稳定地维持在一个较小的变化范围内。特别地，神经网络模型对测试样本3的预测方差首先有一个明显增高的趋势，这是由于当子学习器数量较少时，每新增一个子学习器就会对预测方差带来较大的影响；随着子学习器数量的增加，预测方差最终逐渐趋于稳定，亦表明基于子学习器的判别方法是稳定的。

因此，对于本文中的样本数据和神经网络模型而言，可认为将子学习器的数量设置为8个或以上，能达到较好的判断效果；对于其他样本数据，同样可依据上述方法研究适合的子学习器数量。

04

结论

本文建立了映射式与补偿式两种融合“试验-仿真”标定数据的多级神经网络架构，并提出了在多级神经网络中嵌入子学习器以识别对样本认知程度的方法，形成了精度高、适用性广、能够预警不可靠输出的机翼应变载荷关系神经网络模型，并利用某缩比机翼的有限元仿真及地面标定试验对上述模型进行了验证。研究得到的具体结论如下：

1.相比于仅使用地面标定试验数据建立机翼的应变载荷关系神经网络模型，融合“试验-仿真”标定数据可以显著提升预测精度，且补偿式架构的载荷预测效果优于映射式架构。

2.与仅使用地面标定试验建立的应变载荷关系模型相比，基于补偿式架构的应变载荷关系神经网络模型最高可以将弯矩、剪力、扭矩的预测均方根误差降低86.10%、41.76%、75.75%。

3.子学习器方差法能够度量应变载荷关系神经网络模型对样本的认知程度，有效判别出型在训练阶段学习得不够充分的样本，从而对其不可靠预测结果做出预警。