湍流-化学作用的喷雾燃烧模拟 基于OpenFOAM的FGM模型实现与分析

引言

喷雾燃烧是内燃机研究领域中一个重要且富有挑战性的课题。本文重点讨论柴油喷雾燃烧，其特点是高温非预混燃烧。为了加深对内燃机的理解以便更好地对其进行设计，必须考虑详细的化学机理和TCI（turbulence-chemistry interaction）效应。准确地模拟非预混喷雾自点火和氧化过程以及污染物排放，特别是多环芳烃物种的演化过程，详细的化学计算至关重要。

许多TCI模型已被应用于喷雾火焰的建模。例如，输运概率密度函数(TPDF)方法、代表性交互火焰面(RIF)、火焰面/进度变量(FPV)模型、火焰面生成流形(FGM) 和建表火焰面模型(TFM)。

在这些湍流燃烧模型中，基于火焰面思想的模型具有计算效率高的特点，因此可以使用详细的化学反应动力学。火焰面方法的基本思想是，多维湍流火焰可以看作是嵌入在湍流流场中的被拉伸的一维层流火焰(称为火焰面)的集合。引入混合分数Z以消除非线性化学反应源项求解的困难。由此，化学可以在混合分数坐标下求解，然后映射到流场。基于火焰面的模型与化学建表方法相结合，通过将3D-CFD和层流火焰面计算解耦，降低了计算成本。这使得火焰面模型能够使用复杂化学反应机理，且计算成本相对较低。此外，基于火焰面的模型能够通过预设概率密度函数（PDF）有效地解释TCI现象。只当特征化学时间尺度比混合时间尺度短时，火焰面假设才是有效的，就像在大多数相关条件下类似柴油的燃烧一样。

本文使用FGM燃烧模型对正十二烷燃料的ECN sprayA进行RANS模拟。此外，由于传统观点认为高温非预混燃烧受限于混合过程，其进度变量的方差很大程度上依赖于混合物的形成速度，因此进度变量的方差经常被忽略。本研究考虑了进度变量的方差，类似于预混系统中进度变量的处理。

本研究的目的是为了增进对自动点火过程的了解，并揭示混合分数的变化和进度变量对自动点火过程和火焰结构的影响。

1、数值方法

1.1 气象模拟

FGM (Flamelet Generated Manifolds) 模型与火焰面方法具有相同的思想，即多维火焰可被视为一维火焰的集合。FGM模型的特征还在于存储和检索过程。除了混合分数之外，本研究引入了另一个控制变量，即反应进度变量来考虑不稳定过程，这可以捕捉喷雾燃烧中的自燃现象。本研究中使用的FGM模型可以总结为如下步骤：

(1) 一维火焰面原型的计算。

(2) 一维火焰面的解到控制变量空间的变换。

(3) 采用预设PDF法进行PDF积分。

(4) FGM表的存储。

(5) 根据控制变量及其脉动的三维控制方程求解得到数据库的索引，从FGM数据库中检索热化学量。

1.2 湍流化学相互作用

采用Bilger的公式计算混合分数:

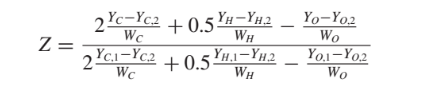
上面Y和W分别是质量分数和分子质量。下标C、H、O分别表示碳、氢、氧元素，下标1、2分别表示纯燃料和纯氧化剂。

2、配置和计算设计

2.1 ECN Spray A

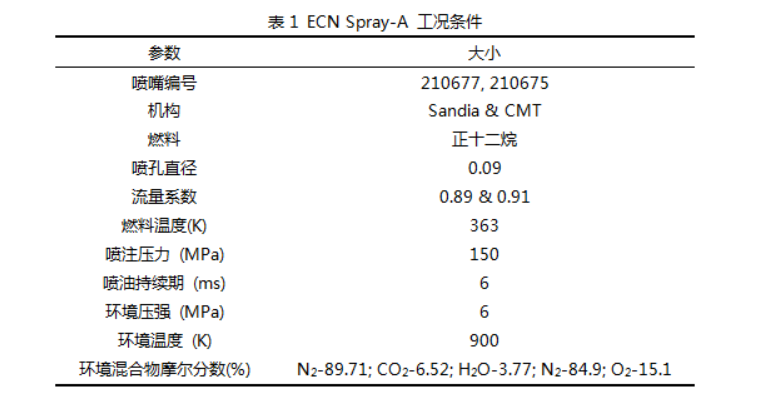
本文所研究的喷雾燃烧案例是在ECN Spray A基准条件下进行的实验，如表 1所示。详细的实验数据分别来自Sandia和CMT的非反应案例和反应案例。根据ECN的建议，喷油型线是从“虚拟喷油型线生成器”中获得的。

2.2 计算设置

本研究开发的新型求解器基于开源CFD框架OpenFOAM的标准喷雾求解器sprayFoam。笔者为FGM存储和检索算法创建了新的库，并将它们动态链接到用于喷雾燃烧的自定义求解器。用非定常雷诺时均法 (URANS)在欧拉框架中描述气相。压力和速度方程由PIMPLE算法耦合，该算法结合了著名的PISO和SIMPLE算法，确保了稳定性和准确性。液相被认为是由单个包裹组成的离散相，并使用拉格朗日粒子跟踪（LPT）处理。

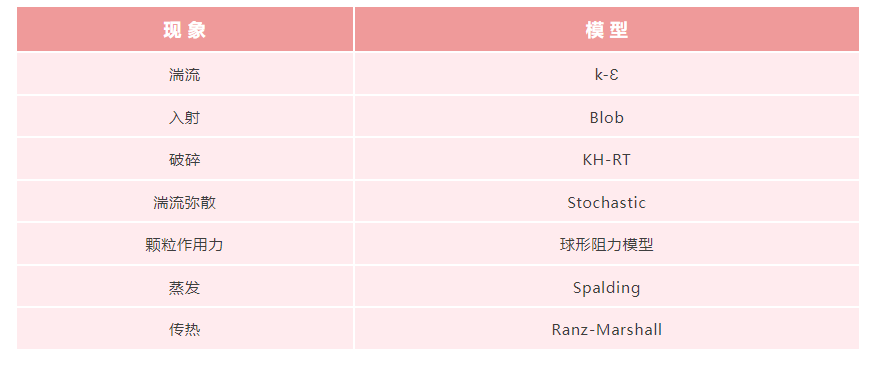
计算采用的网格为沿着喷雾流经区域局部细化的非均匀3D网格（图 1），以定义定容燃烧弹的计算域，每侧尺寸为108mm。时间步长固定为5E-7s，模拟结束时间设定为1.5 ms，此时火焰已形成准稳态结构。湍流和喷雾子模型的细节总结在表 2中。

图 1 (a) 计算网格 (0.25mm) ；(b) 局部放大

表 2  模拟中运用的相关子模型

3、模拟结果

3.1 无反应喷雾案例的验证

拉格朗日颗粒追踪法(LPT) 因实现难度较小，计算量相对较小而被广泛应用于高压喷雾模拟。然而，很多报告指出欧拉-拉格朗日的喷雾模拟计算的精度与网格大小密切相关。为了保证网格的独立性，本研究采用了5种网格，网格尺寸为0.125mm、0.25mm、0.5mm、1mm和2 mm，网格量分别为9081414、1444631、321376、172962和157464。这5种网格数量是通过五个不同水平的局部细化得到的，全部基于2mm的基础网格，以正确地解析流动细节。图1给出了网格划分(0.25 mm)，显示了细化和局部细节。从图中可以看出，更细的网格可以预测更长的液相贯穿距，最后两种网格数量具有相似的性能，但在喷雾演化开始时只有很小的差异。气相贯穿的行为类似。考虑到精度和效率，本文选择了0.25 mm的网格。

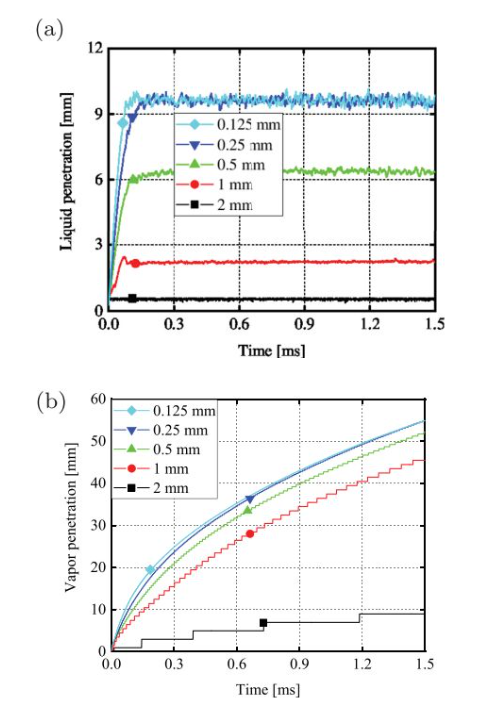
图 2  5种测试网格下计算所得喷雾液相(a)与气相(b)的贯穿距

为了评估当前的湍流和喷雾模型设置，本文针对非反应sprayA基准工况（0％O2）, 基于液相和气相贯穿距以及燃料质量分布的实验数据进行了验证。图 2显示了液相和气相贯穿距随注入开始时间(ASI)的模拟和实验结果。液相和气相贯穿距采用了ECN推荐的定义液相和气相贯穿距被定义为从喷嘴出口到液体体积和蒸汽质量分数达到0.1%的最远轴向距离。

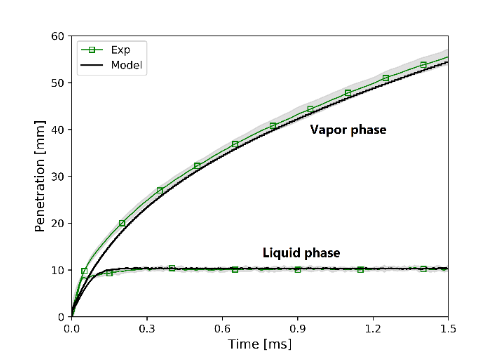
图 3   无反应条件下的液相与气相贯穿距的预测

与实验趋势相比，液相和气相贯穿距可以很好地被预测，只有在注入早期的气相贯穿距有很小的偏差，如图3所示。

（a）

（b）

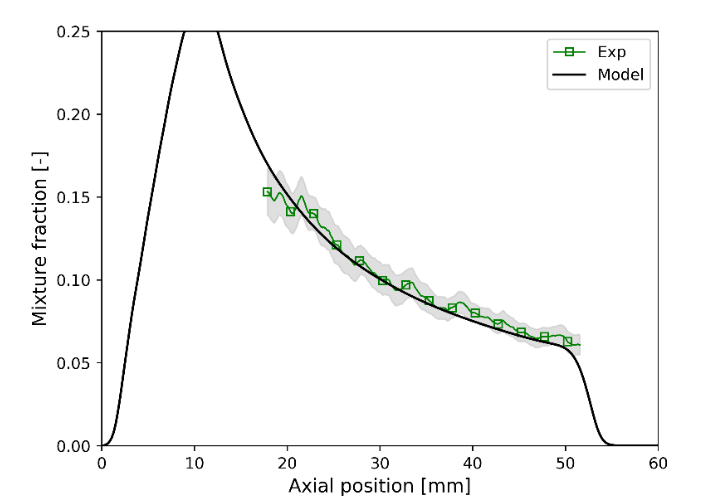
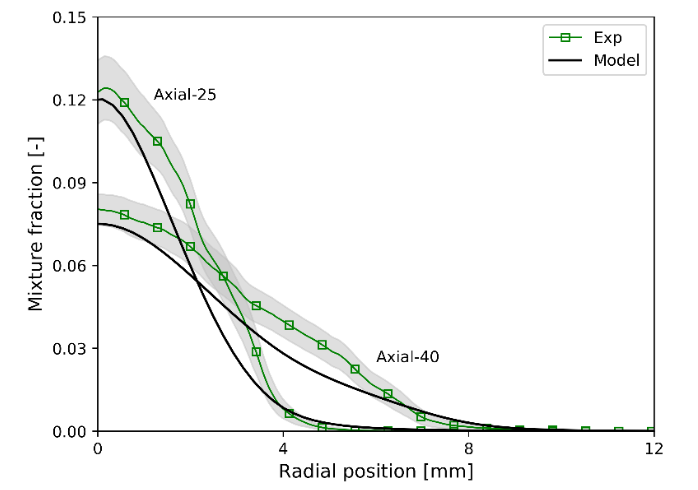
图4  混合物分数的轴向和径向分布 

图4显示了混合分数的轴向和径向分布，其中径向剖面取样于喷油器下游25mm和40 mm处。在图4中，平均剖面周围的阴影区域对应于测量的混合分数的标准差。图中混合分数的预测值与实验测量值吻合较好。预测的和测量的平均混合物分数之间的差异完全在实验结果误差范围内，只是喷雾的径向外围距离喷射器出口40 mm处的混合物分数略有不足。

3.2 全局点火

喷雾演化初期 (t = 0.2 ms)，由于蒸发和燃料-空气混合，温度几乎沿绝热混合线分布，没有发现明显的温度升高，如图5所示。但在贫燃料区仍有进度变量源项出现，这表明早期反应的发生。自点火前的这段时间为点火延迟期，其持续时间受局部燃料-空气混合物和标量耗散率的影响。

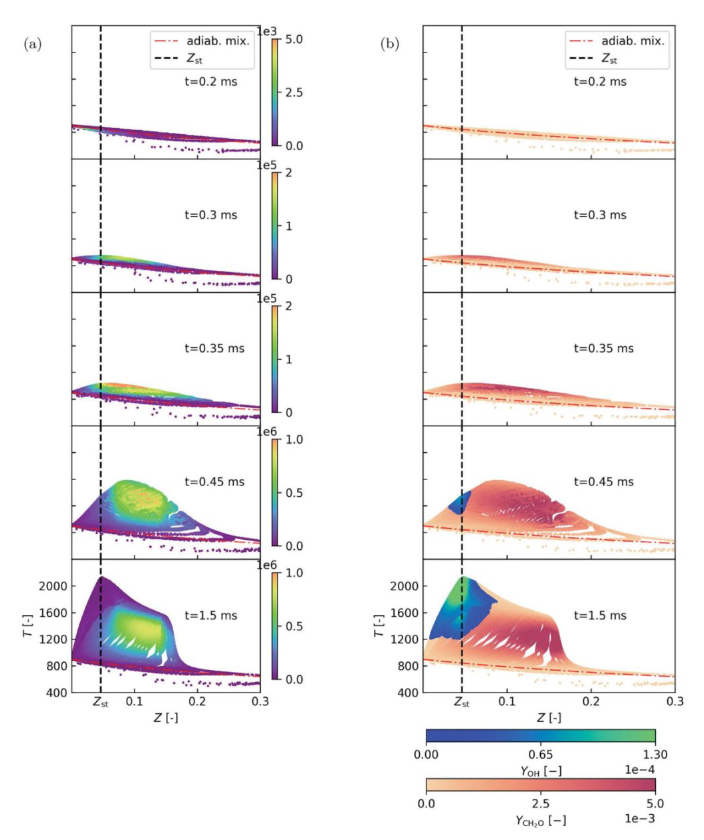
图5 ZT平面散点图：(a) 按

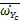
染色；(b) 按CH2O及大于2%的OH叠加染色（红线代表绝热混合线，黑线代表）

图5第二行显示，在t=0.3ms时，化学计量混合物分数线(Zst= 0.0463242)附近的温度开始显著超过局部绝热温度。CH2O出现在Zst附近，其进度变量源项比在t=0.2 ms时多两个数量级。在图 5 (b)的第三行，可以观察到CH2O被输送到更丰富的混合分数区域，这就是所谓的火焰传播。整个反应区温度升高，在第四行的Z=0.1处达到最大值，这就是所谓的第二阶段点火。还观察到OH浓度在化学计量条件附近显著增加，高温区向Zst线方向移动，混合分数区更加稀薄，最终形成一种高温准稳态扩散火焰，其中CH2O主要出现在富燃区，OH集中在Zst线附近，保持了上升火焰的稳定。在这一阶段，许多分散的粒子靠近平衡线(图中未显示)，特别是在Zst线附近。

3.3 湍流-化学反应相互作用(TCI)对点火过程的影响

为了阐明Z和C的β-PDF的影响，本研究还进行了另外两种情况的分析，其中δ-PDF分别用于Z和C。这三种情况的点火延迟时间（IDT）在表 3中被列出，其中βz–βc是基准情况，这意味着β-PDF用于Z和C，而δz-βc表示δ-PDF用于Z，βz–δc表示将δ-PDF用于C。研究的点火延迟时间定义为温度最大梯度的时间。

应用β-PDF意味着应包括方差才能计算PDF，而在δ-PDF中不考虑方差。表3表明，在混合分数和反应进程变量存在变化的情况下，点火延迟发生了变化。与基线情况相比，当将δ-PDF用于Z时，IDT变短。相反，当δ-PDF用于C时，IDT会稍长一些。也就是说，考虑Z方差会延迟点火，而考虑到C方差将会促进点火。

在3D求解器中，从FGM表差值得到的最重要的变量是进度变量源项

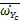
，它决定了反应进程和点火延迟时间。

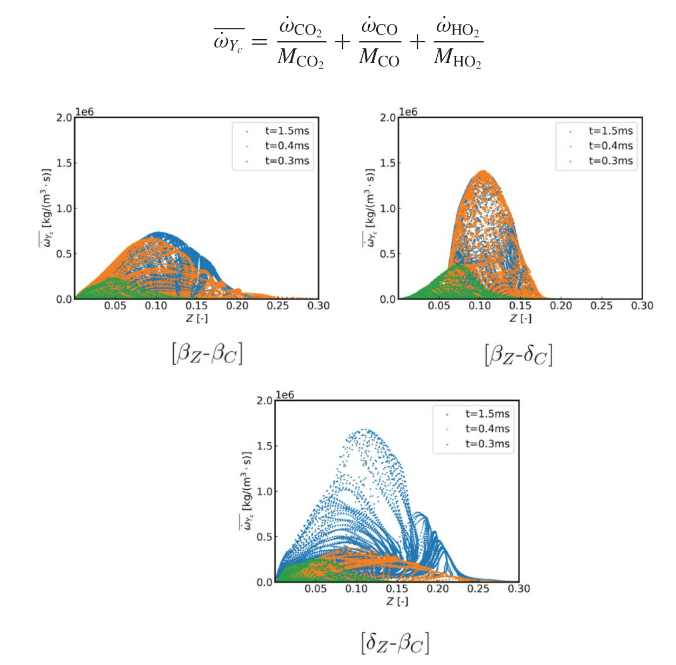
图 6  三个算例中进度变量源项变化与间的关系

尽管在βz–βc和βz–δc情况之间，整体点火特性（点火延迟时间）差异很小，但差异在反应进度变量源项的时间演变中更为明显（图 7（a））。图 7（b）中显示了提取进度变量源项峰值的单元格中的混合分数及其时间演变。图 8给出了三个阶段中进度变量源项与进度变量的关系。

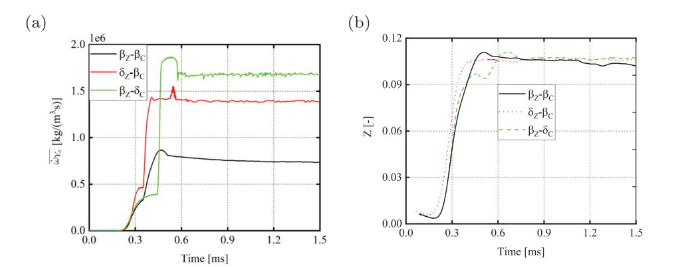
图 7 （a）反应进度变量源项最大值随时间演变过程；（b）提取进度变量源项峰值的单元格中的混合分数及时间演变

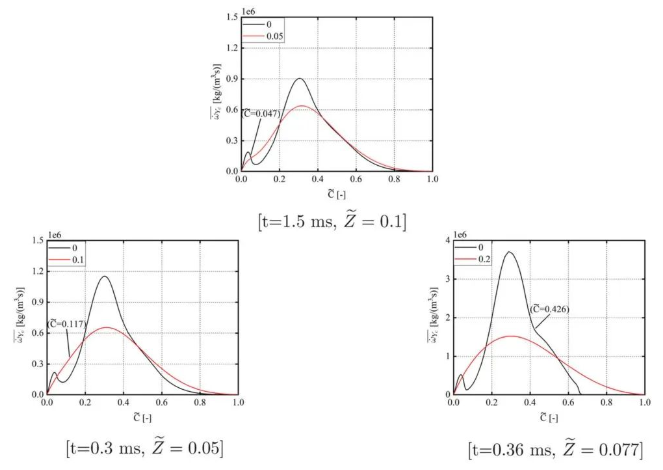
图 8  三个阶段中进度变量源项与进度变量的关系

3.4 TCI对火焰结构的影响

本研究发现，在稳态条件下，混合分数和进度变量的变化也会改变火焰的结构。图 11显示了从βz–βc，δz–βc和βz–δc情况获得的结果在1.5 ms ASI时计算出的OH质量分数分布。

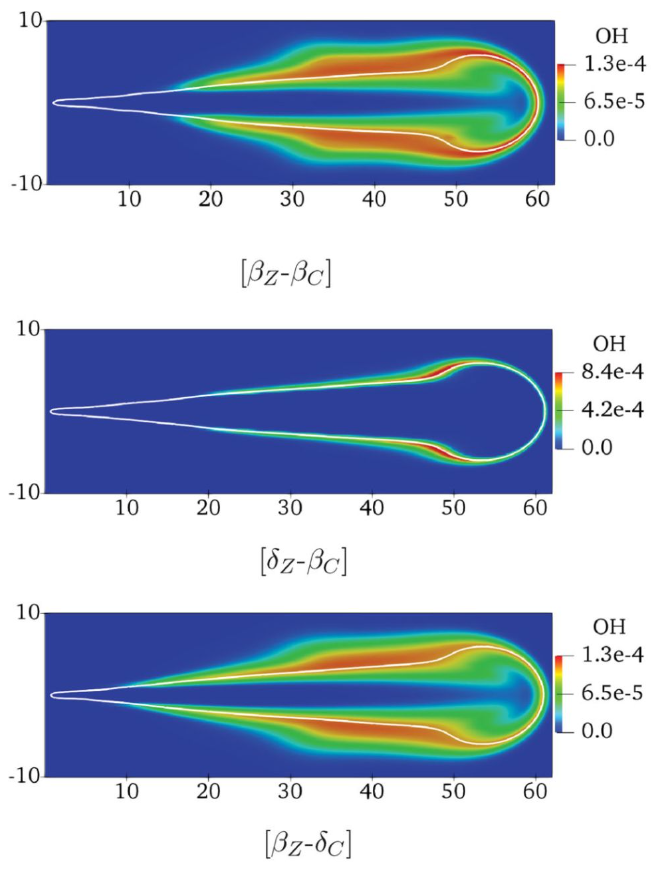
图 11  三个阶段中进度变量源项与进度变量的关系

如图 11所示，在βz–βc和δz–βc案例之间，OH质量分数分布存在显着差异。与δ-PDF相比，Z-的β-PDF的OH质量分数的峰值要低得多。另一方面，考虑到混合比例的变化，β-PDF预测了空间中更多的OH质量分数分布。而PDF的火焰相对较薄。在使用mRIF，FGM，TFM和TPDF模型的其他ECN喷雾（正庚烷或正十二烷）燃烧模型中也报告了相同的发现，这归因于这些研究中的湍流波动。至于进度变量方差的影响，图 11中的OH质量分数分布表明，在βz–βc情况和βz–δc情况下，火焰结构和OH质量分数最大值相似。也就是说，进度变量的方差对火焰结构的影响很小。然而，从图 11(c)中可以明显看出，它使火焰浮起长度变短。在采用非定常FPV模型的浮起的自燃火焰模拟中，也发现了进度变量方差的类似影响。

4、结论

ECN喷雾的RANS模型是使用最新开发的FGM燃烧模型进行的，该模型允许在喷雾燃烧模拟中应用详细的化学机理。对无反应的情况进行数学模型验证，以验证网格无关性和喷雾子模型。发现最小单元尺寸为0.25 mm的网格分辨率与液相和气相贯穿距和混合分数分布的实验结果一致。整体点火过程表明，早期反应发生在稀燃侧，并且第一阶段点火在接近化学计量条件下开始，并传播到更浓的混合物中，在此促进点火，这是冷火焰传播的特征。然后，第二阶段点火发生在富燃侧。最后，稳定的扩散火焰形成，稳定的火焰结构在文中也被进一步研究。

混合分数的方差已经被许多研究者所重视。在当前的研究中，我们发现忽略混合分数的变化会缩短点火延迟时间，并导致非常薄的火焰结构。此外，随着质量分数的变化，OH质量分数的峰值大大降低。正是β-PDF导致了OH质量分数的广泛分布。在不同的进度变量下，进度变量源项沿混合分数坐标的分布是单峰的，OH质量分数也是如此。在将β-PDF应用于混合分数之后，最大值将分布到其他区域，并且整个分布变得更宽。由于混合控制特征，在喷雾燃烧模型中经常忽略的进度变量方差也对自燃和火焰结构有影响。忽略进度变量的方差会延迟自动点火并缩短火焰浮起长度。