

半导体雷射导通延迟时间
描述
当半导体雷射从阈值条件以下要达到雷射的操作,其主动层中的载子必须要先达到阈值载子浓度才会有雷射光输出,这段载子累积的时间称为导通延迟(turn-on delay)时间,表示为Td。使用(4-1)式,假设雷射操作在阈值条件以下,我们可以假设np=0,以及假设载子生命期Tn为定值,因此主动层中的载子浓度速率方程式为:

假设电流密度的注入可以表示为:

其中Jb为电流密度的起始偏压值,Jp为电流密度增加的值,u(t)为步阶函数,当 t<0时,u(t)=0,当t≥0,u(t)=1。当 t=0时,电流密度的初始值为:

当t≥0,J(t)=Jb+Jp=J,解(4-78)式可得:
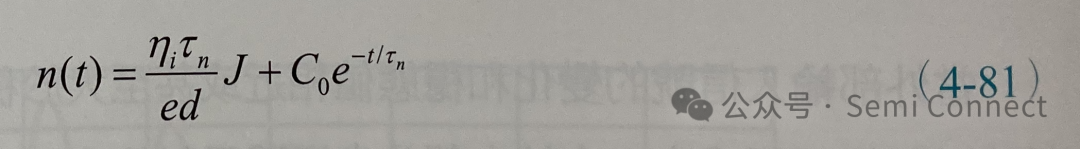
(4-80)式为边界条件带入上式可解得C0,
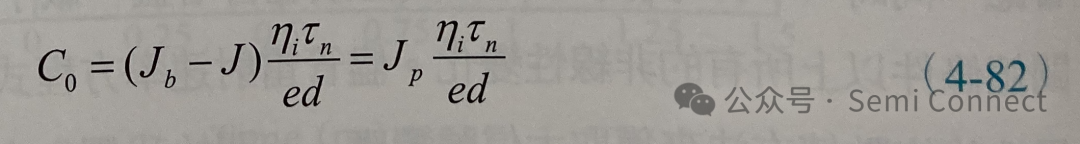
因此,载子浓度在t≥0的变化为:
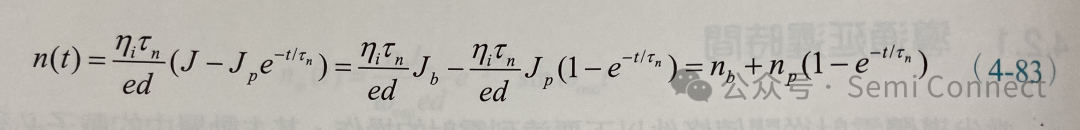
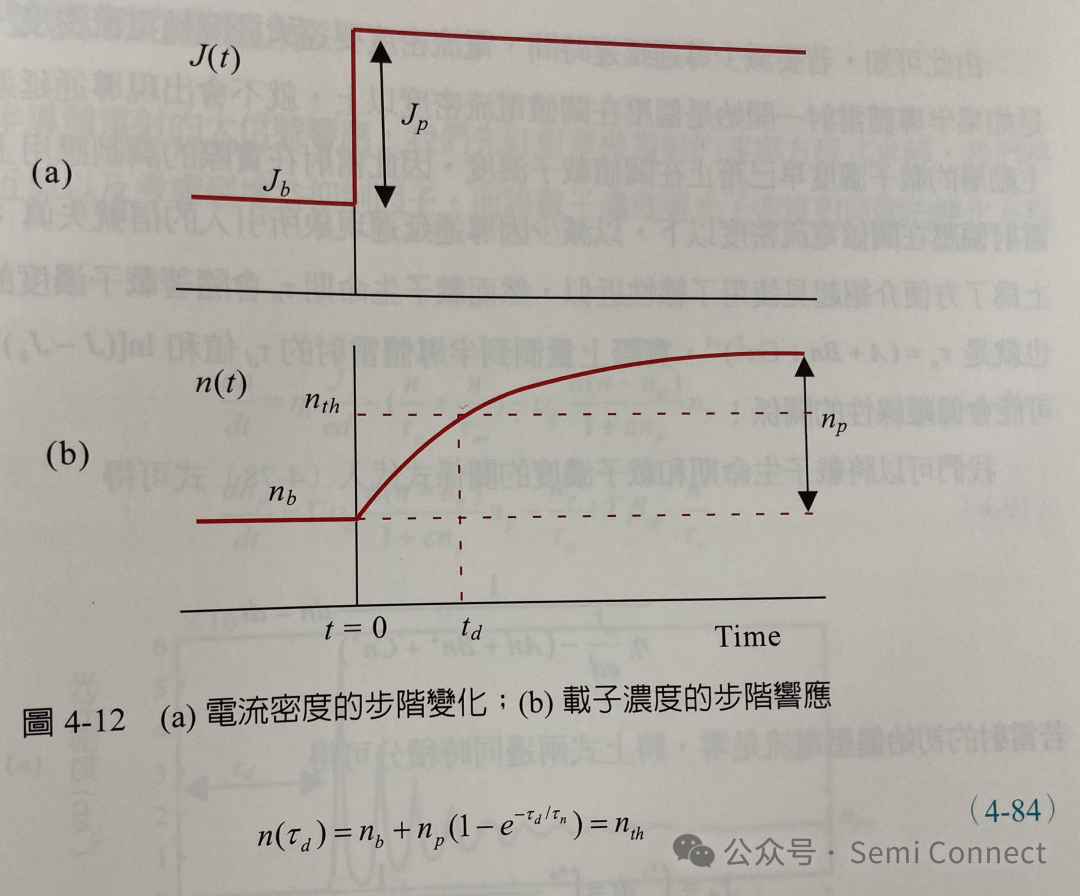
如图4-12所示,主动层中的载子浓度随着时间演进逐渐累积到 nb +np的值,载子浓度增加的速度和载子生命期Tn有关,若Tn愈小,则载子浓度增加的速度愈快。
若载子浓度在到达 nb +np的值之前就先到达了阈值载子浓度nth,雷射开始操作,大于阈值载子浓度nth的部分都会迅速遭遇受激复合放出光子,使得载子浓度不再随如图4-12(b)的趋势增加,而是钳止在nth的值,而到达阈值载子浓度 nth的时间即为雷射的导通延 时间Td,我们可以由(4-83)式求出 Td为:
用电流密度来表示为:

因此

我们可以借由量测在不同电流操作下的Td値,由(4-86)式将Td値和In[(J-Jb)/(J-Jth)]作图将可以得到载子生命期Tn;若Jb趋近于零,(4-86)式可以简化为:

由此可知,若要减少导通延迟时间,电流密度要远大于阈值电流密度。最后要注意的是如果半导体雷射一开始是偏压在阈值电流密度以上,就不会出现导通延迟的现象,因为主动层的载子浓度早已钳止在阈值载子浓度,因此雷射在实际的调制应用上,都会避免将雷射偏压在阈值电流密度以下,以减少因导通延迟现象所引入的信号失真;此外,我们以上为了方便介绍起见使用了线性近似,然而载子生命期Tn会随着载子浓度的变化而改变,可能会偏离线性的关系!
我们可以将载子生命期和载子浓度的关系式代入(4-78)式可得
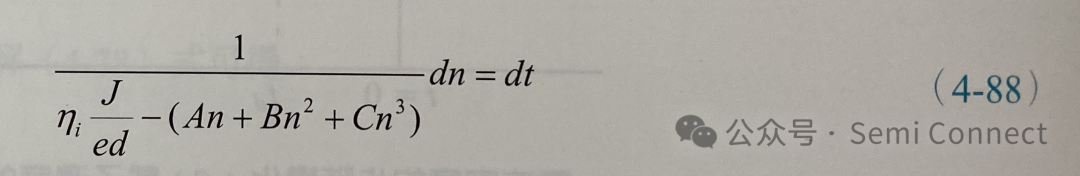
若雷射的初始偏压电流是零,将上式两边同时积分可得
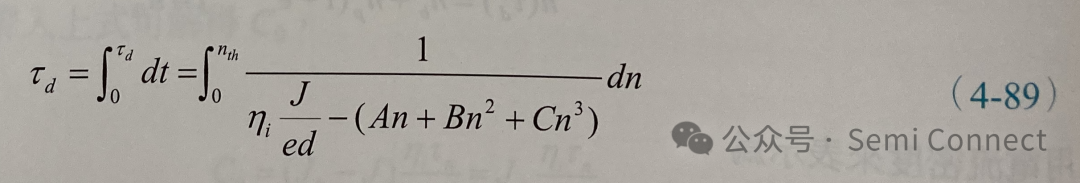
借由量测到不同输入电流下的导通延迟时间,使用上式可以拟合出影响载子生命期的参数。
-
半导体器件原理与仿真设计: 基区输运延迟时间常数#半导体学习电子 2022-11-10
-
请问如何生成准确的延迟时间?2020-12-02 0
-
怎么实现IGBT延迟导通时间测量系统的设计?2021-05-14 0
-
有没有办法减少LVDS输出的延迟时间?2023-05-25 0
-
由模拟信号控制脉冲延迟时间2009-03-29 957
-
梳妆滤波器延迟时间Td的演示2009-07-31 745
-
延迟时间的确定2009-07-31 1450
-
关于IGBT导通延迟时间的精确测量方法2009-11-23 2221
-
MT-007: 孔径时间、孔径抖动、孔径延迟时间——正本清源2021-03-21 877
-
怎么测试开关电源开机延迟时间?测试方法是什么?2023-11-16 1450
-
开机延迟时间测试步骤与测试标准介绍2023-11-17 1767
-
孔径时间、孔径抖动、孔径延迟时间介绍2023-11-27 303
-
半导体雷射震荡条件2024-12-19 186
-
半导体雷射之发光线宽2025-01-08 74
-
半导体雷射相对强度杂讯2025-01-09 82
全部0条评论

快来发表一下你的评论吧 !

