
资料下载

电机控制中矢量图的作用(可下载)
一、前言
在电机驱动开发过程中,我们有的时候需要知道相电压与线电压之间的关系,也可能会需要知道 相反电动势与线反电动势之间的关系等,那么为了能够直观的分析出这些矢量的关系(包括幅值关系、 相位关系),我们就可以借助矢量图这个工具了
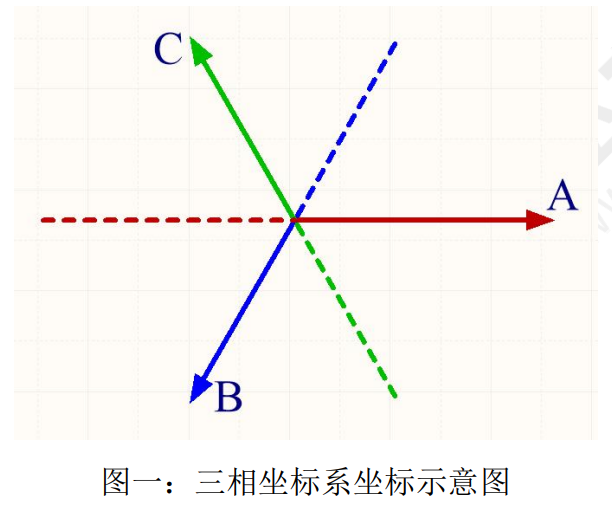
利用矢量图,我们可以很容易根据矢量合成及矢量分解的法则来得出要分析的矢量之间的关系, 就可以用几何加数学的方式找出合成矢量所处的位置或者合成矢量被分解之后的位置。我们甚至通过 矢量图的关系分析之后,再根据反电动势跟转子位置的关系可以得出转子的位置。因此我们了解矢量 图及其相关的法则就很有必要了。如下图一所示为三相坐标系的坐标图示意图:
二、矢量概念介绍
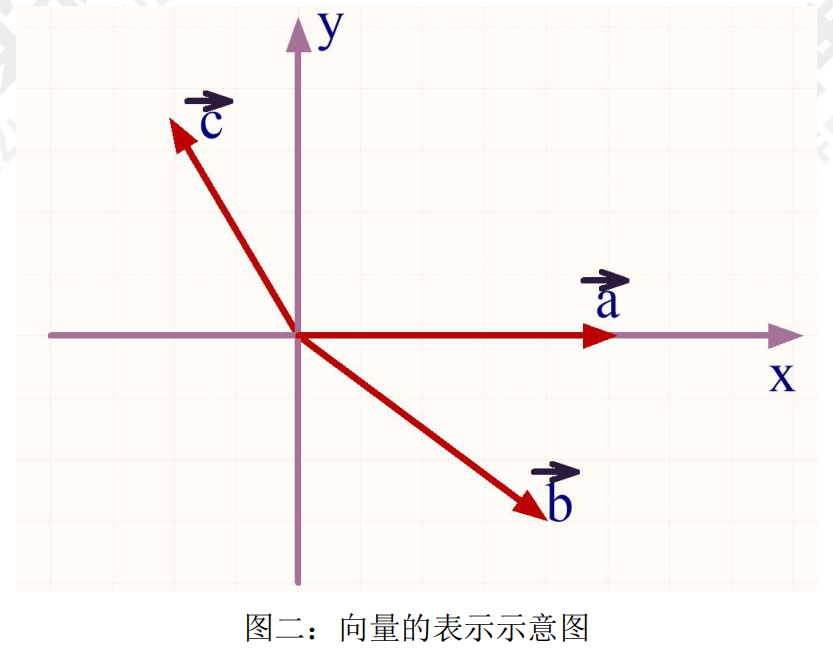
想要学会分析矢量图,我们需要有一些基础知识的铺垫,这里我们有必要简单介绍一下矢量的概 念。矢量这个概念其实最早可以追溯到我们中学课堂里学过的向量,我们都知道,向量是一个既有大 小又有方向的量,向量的运算不在遵循一般的四则运算法则,而是有专门的运算方式,下图二所示为 我们中学向量的表示方式:
而矢量这个概念其实到大学课本才接触到,它的定义是,有的物理量,既要有数值大小,又要有 方向才能确定完全确定。这些量不遵循一般的代数法则,而遵循特殊的运算法则。这样的量被称为物 理矢量。其实向量这个概念在数学课本用得比较多,在物理课程中就有了另一个名字“矢量”。只不过 在物理学中,会有很多物理量如力,它有大小和方向,电压,也有大小和方向,用来表示物理量的大 小和方向就被称为了矢量,而数学只是研究某个有方向和大小的量的运算及表示形式,因此就把它称 为了向量。所以,对于我们工程师来说,可以理解它们就是一个东西。
三、矢量的运算法则
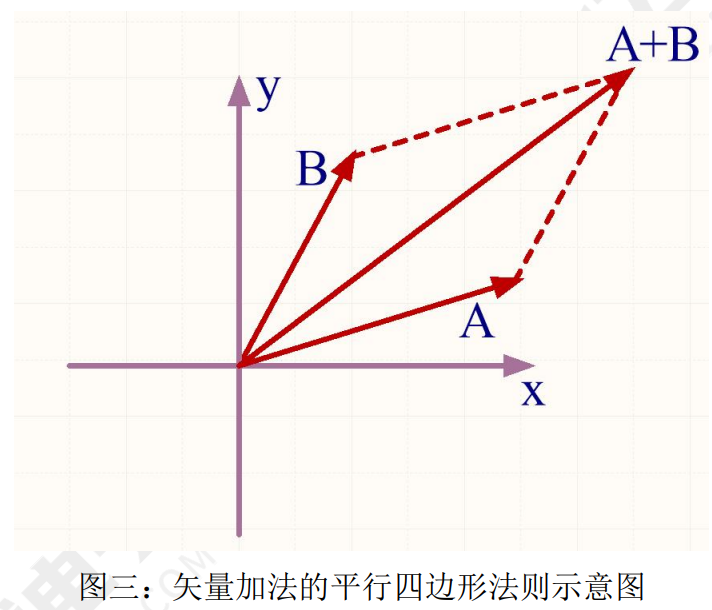
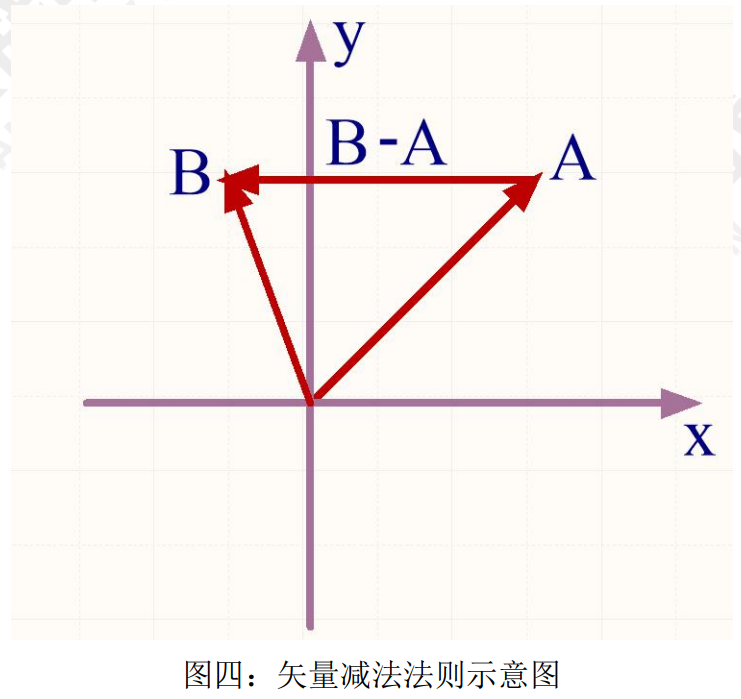
矢量之间的运算要遵循特殊的法则。矢量的加法可以一般可以使用平行四边形法则,当然也可以 推广到三角形法则或者正交分解法。矢量减法是矢量加法的逆运算,一个矢量减去另一个矢量,等于 加上那个矢量的负矢量。
矢量也可以进行乘法运算,矢量和标量的乘积仍为矢量,矢量和矢量相乘,可以得到一个新的标 量(只有大小,没有方向的量),这样得到的结果是标积;两个矢量相乘也可以得到一个新的矢量,把 这样的乘法称为矢积。其实就对应着中学课本中学习的向量的内积和外积。
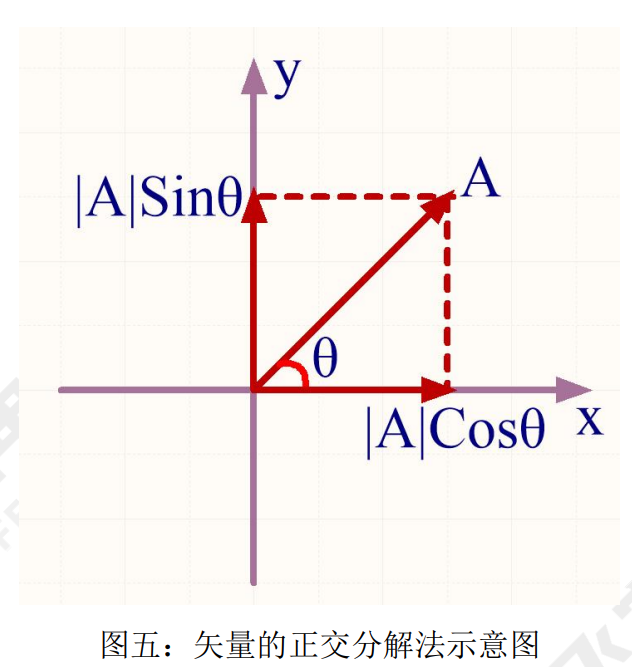
在电机控制中,基本上以上三种方式使用得比较多,其实在遇到减法得场合,都是转换为加法进 行合成
四、反电动势矢量合成
在电机控制系统中,我们可以基于定子三相绕组建立三相基本坐标系,在这个坐标系中可以进行 矢量合成与分解的分析,从而可以知道反电动势之间的关系
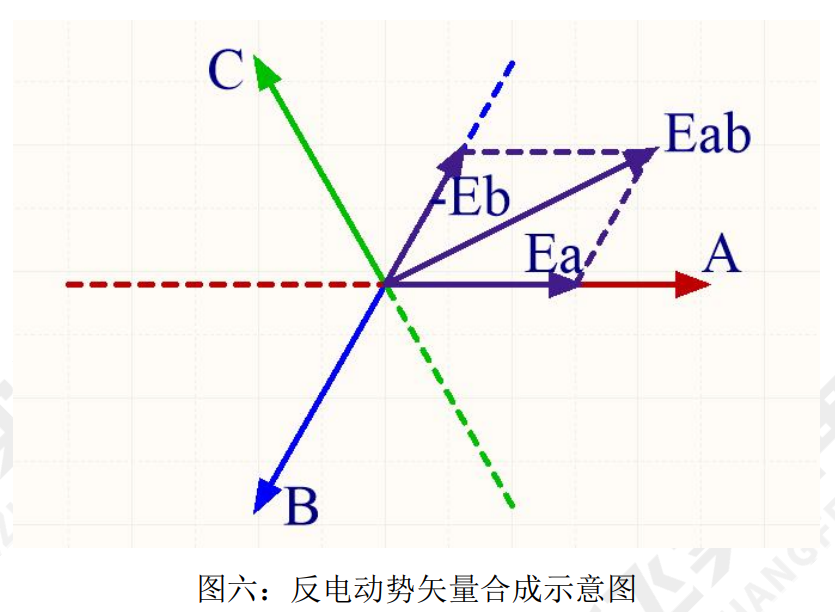
如上图六所示,我们知道了 Ea 及-Eb 相反电动势的大小及方向,利用平行四边形的法则可以得出 线反电动势的的大小及方向。在上图坐标系中,我们假设顺时针旋转为角度超前,从上图中可以得出 先线电动势 Eab 超前相反电动势-Eb 30 度,相反电动势 Ea 超前线反电动势 Eab 30 度。还可以根据三角 形的关系将合成得到的线反电动势跟相反电动势的幅值关系求出来
在 SPWM 及 SVPWM 算法中,我们就需要知道相电压跟线电压的关系,从而推导出两种算法的电 压利用率问题,所以我们了解矢量图的合成与分解原理,就可以很方便的知道矢量的关系,也可以很 好的分析出电压利用率的问题。下图七给大家展示了一幅完整的全坐标系内的反电动势合成矢量图:
完整版技术文档请点击文章开头普通下载
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






