

介绍利用贝叶斯统计的一个实践案例
电子说
描述
为了大家可以对贝叶斯算法有更多的了解,人工智能头条为大家整理过一篇关于贝叶斯算法的文章。今天将为大家介绍利用贝叶斯统计的一个实践案例。通项目实践达到学以致用的目的,相信大家对贝叶斯统计的理解和掌握都可以更深入,提炼出更精炼的内容。
▌前言
我来自越南,在新加坡上高中,目前在美国上大学。我经常听到身边的人取笑我看起来很“娇小”,我应该怎样做运动,去健身房增重,然后才能有“更好的体格”... ...然而我对这些评论却是怀疑的,对于身高1.69米(5’6)和体重58kg(127lb)的人来说,我有接近完美的 BMI 指数(20.3)。
后来我明白他们没有在谈论 BMI,他们强调的是体型。
想想看,他们的出发点是好的:资料显示越南男性的平均身高与体重是1米62和58kg,鉴于我身高高出了平均值,但体重与越南男性平均体重却相同,我可能会“看起来”更瘦一些。 “看起来”圈起来划重点。 如果体重相同,但是身高更高,那看起来更苗条更修长,这是一件逻辑很简单的事。而我在考虑这是一个值得进一步探究的科学问题。
那么问题来了,在身高1米69的越南男性中,我的体型有多瘦小?
我们需要一种方法论的方法来研究这个主题,一个好方法是尽可能多地找到越南男子身高和体重的数据,看看我的数据处于哪个位置。
▌越南人口概况
在网上搜索后,我找到了一份包含超过10,000名越南人的人口统计信息调查研究数据。 我将样本量范围缩小到18-29岁年龄段的男性。 这使我有383名年龄在18-29岁左右的越南男性的样本,对于接下来的分析来说已经是足够的了。
首先画出人口重量直方图,看看我在越南男性中哪个位置。
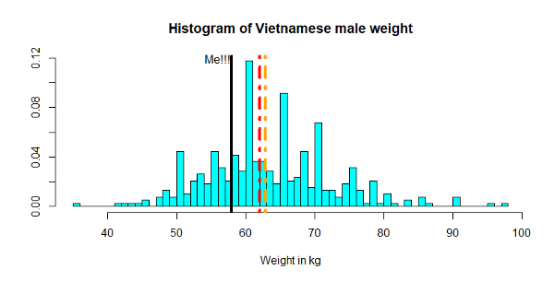
红线显示样本的中位数,橙色线显示均值
这个图表明,我略低于这383名越南青年体重的平均数和中位数。是好消息吗? 然而,问题的重点并不在于我的体重与样本相比如何。假设越南男性人口的健康状况良好,并且整个越南人口可以由这383个人代表,但考虑到1米68的身高因素,我们可以推断出我的体重与整个越南人口相比是什么情况。 为此,我们需要深入研究回归分析。
第一步绘制关于身高和体重的二维散点图。
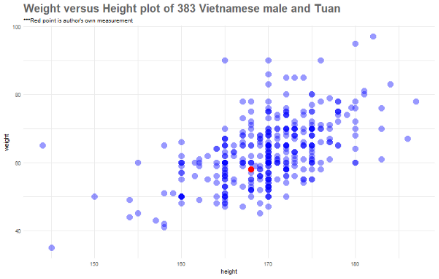
好吧,我的数据看起来处在很平均的位置上。实际上,如果我们只查看那些身高168cm的人的数据(想象一条在168cm处的垂直线,并穿过红点),那么我的体重比这些人稍轻一些。
另一个观察到的重要结果是,散点图的离散程度表明了越南男性的身高和体重之间存在着较强的线性关系。我们将进行定量分析以深入了解这种关系。
我们需要做的是快速添加“标准的最小二乘”线。稍后我会更多地介绍这条线,但现在先展示它。
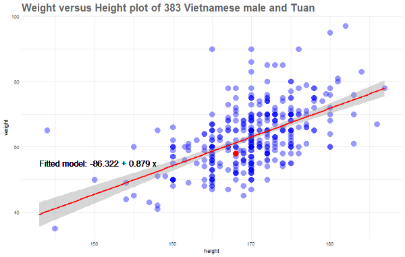
我们的最小二乘线是y = -86.32 + 0.889x,会发现在我这个年龄的越南男性的通常情况是,高1厘米体重就会增加0.88千克。
但是,这并不能回答我们的问题。在身高为1米68时,58公斤的体重会被认为是太重,太轻或只是平均? 为了更加定量地解释这个问题,如果我们有一个身高为1米68的人的分布,我的体重下降到25,50或75个百分点的几率是多少? 要做到这一点,需要我们深入挖掘并理解回归背后的理论。
▌线性回归的理论
在线性回归模型中,Y变量的预期值(在我们的例子中,人的体重)是X(高度)的线性函数。 我们称之为线性关系,其中 β0 和 β1 分别是截距和斜率; 也就是说,我们假设E(Y | X = x)= β0 + β1 * X。 但是我们不知道 β0 和 β1 的值,因此它就是未知参数。
在最标准的线性回归模型中,我们进一步假设给定 X = x下Y的条件分布是正态分布的。这意味着简单的线性回归模型:
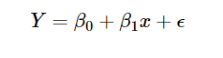
可以写成下面的形式,注意,在许多模型中,我们可以用精度参数 τ 替换方差参数 σ,其中 τ = 1 / σ。
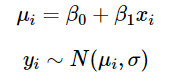
总结:因变量 Y 服从满足平均值 μi 和精度参数 τ 的正态分布。 μi 与由 β0 和 β1 参数化的 X 是线性关系
最后,我们还假设未知方差不依赖于 x ; 这个假设被称为同方差。
上述内容可能有点多,可以在下面这张图中看到刚讨论过的内容。
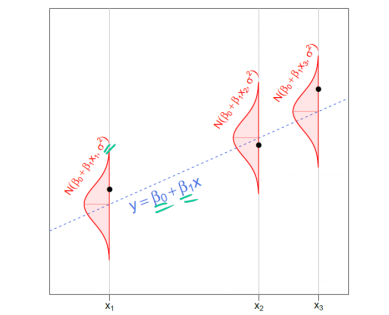
在实际的数据分析问题中,我们只给出黑点(数据)。我们的目标是使用这些数据,对我们不知道的事情做出推断,包括 β0,β1(阴影,蓝色虚线)和 σ(红色正常密度的宽度)。 注意每个点周围的正态分布看起来完全相同。 这是同方差性的性质。
▌参数估计
现在,你可以通过几种方法来估计 β0 和 β1。如果你使用最小二乘法来估计此类模型,则不必担心概率公式,因为你搜索 β0 和 β1 的最优值的方式是使拟合值与预测值的平方误差最小化。另一种,可以使用最大似然估计来估计这种模型,你可以通过最大化似然函数来寻找参数的最优值。
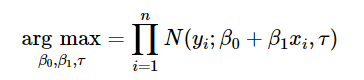
注意:一个有趣的结果是(这里没有数学证明),如果我们进一步假设误差也属于正态分布,则最小二乘估计量也是最大似然估计量。
▌使用贝叶斯观点的线性回归
贝叶斯方法不是单独最大化似然函数,而是假设了参数的先验分布并使用贝叶斯定理:
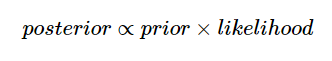
似然函数与上面的相同,但是不同之处在于对待估计参数β0,β1,τ假设了一些先验分布并且将它们包括到了等式中:
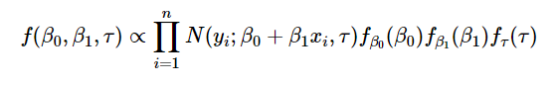
“ 什么是先验,为什么我们的方程看起来复杂了10倍?”
相信我,这个先验信息虽然看起来感觉有点奇怪,但它非常直观。事实是,有一个非常强烈的哲学推理,为什么我们可以使用一些看似任意的分布来确定一个未知参数(在我们的例子中是β0,β1,τ)。这些先验分布是为了在看到数据之前捕捉我们对数据分布特点的看法。在观察一些数据之后,我们应用贝叶斯规则来获得这些未知参数的后验分布,它考虑了先验信息和数据。从这个后验分布我们可以计算数据的预测分布。
这些先验分布是为了表达我们在看到数据之前,对数据分布特点的一种假设
最终的估计值将取决于(1)你的数据和(2)先验信息,但数据中包含的信息越多,先验信息的作用就越小。
“所以我可以选择先验分布吗?”
这是一个很好的问题,因为有无限的选择。 (理论上)只有一个正确的先验,即表示你的先验假设。然而,在实践中,先验分布的选择可能相当主观,有时甚至是任意的。 我们可以选择标准偏差较大的正态先验(小精度)。例如,我们可以假设 β0 和 β1 是来自均值为 0 和标准差为 10,000 的正态分布。这被称为无信息先验,因为基本上这种分布将是相当平坦的(即,它为特定范围内的任何值分配几乎相等的概率)。
接下来,如果这种先验分布是我们的选择,我们不必担心哪个分布可能会更好,因为它的形状几乎都是平坦的,并且后验分布并不关心先验分布的分布情况特点。
同样,对于精度 τ,我们知道这些必须是非负的,所以选择一个限制为非负值的分布是有意义的。例如,我们可以使用低形状和尺度参数的 Gamma 分布。
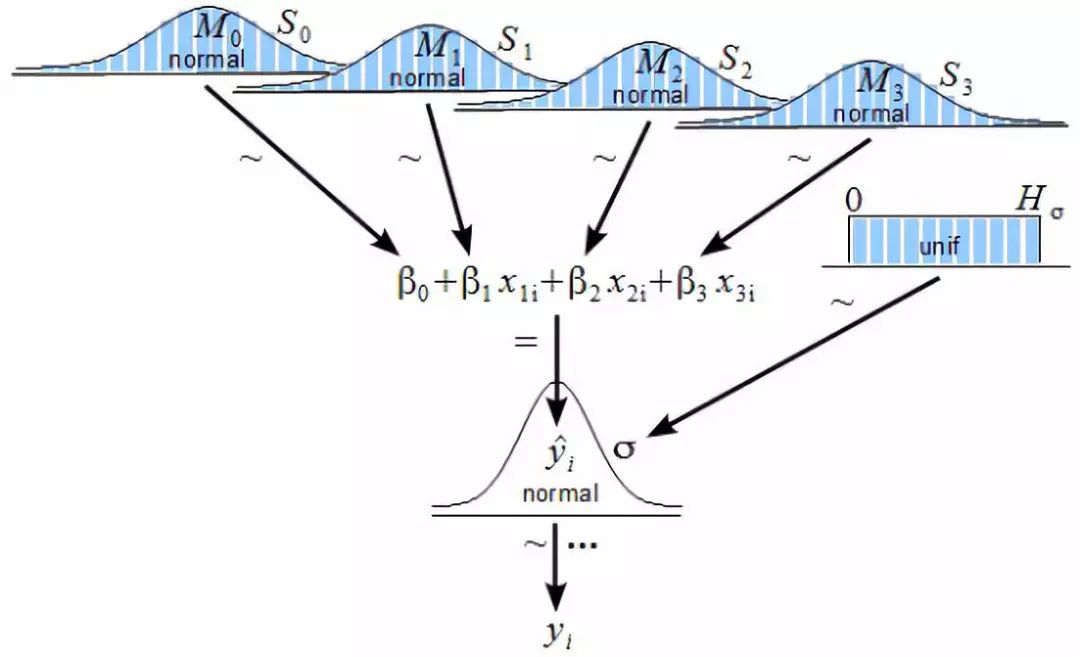
另一个有用的非信息选择是均匀分布。如果你选择σ或τ的均匀分布,你可能会得到John K. Kruschke所说的模型。
▌用R和JAGS进行仿真
迄今为止这个理论非常好。求解方程在数学上具有挑战性。 在绝大多数情况下,后验分布不会直接可用(正态分布和 Gamma 分布是多么的复杂,你必须将其中的一系列数据乘在一起)。
马尔可夫链蒙特卡罗方法通常用于估计模型的参数。JAGS工具包帮助我们做到了这一点。
JAGS工具是基于马尔可夫链蒙特卡罗(MCMC)的仿真过程,能产生参数空间 θ =(β0;β1;τ)的许多迭代结果。 在该参数空间中为每个参数生成的样本分布将接近该参数的总体分布。
为什么会这样? 解释非常复杂。简单的解释就是:MCMC通过构建具有目标后验分布的马尔可夫链,从而在后验分布中生成样本。
讲真它并不好玩。 与通常解析方程(2)的方式不同,我们可以做一些聪明的抽样,从数学角度证明我们样本的分布是 β0,β1,τ 的实际分布。
▌如何使用这个JAGS工具呢
我们在R中通过如下步骤运行JAGS
第一步,我们用文本格式编写我们的模型:
然后,我们使用JAGs进行模拟。在这里,我设定 JAGs 模拟参数空间θ 10000次的值。在这样的采样之后,我们可以得到如下所示θ=(β0;β1;τ)的采样数据。
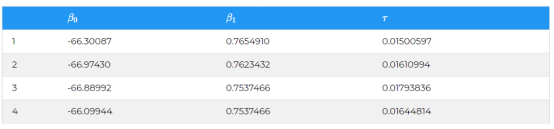
现在我们对参数空间θ进行10,000次迭代,记住通过公式:
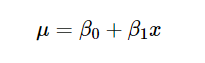
这意味着,如果我们用 x = 168 cm 代替每次迭代,我们将找到 10,000 个体重值,并且因此给出高度为 168 cm 的体重分布。
我们现在是在给定身高条件下,计算我体重的百分位。我们能做的就是根据我的身高找到我体重百分位数的分布。
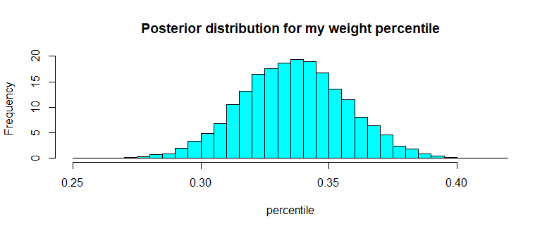
现在,这个图告诉我们的是,我的体重(给定168厘米的身高)最有可能位于越南人口模拟数据的0.3%左右。例如,我们可以找到我的体重在前40个百分点或更少的百分位数。
所以绝大多数证据表明身高168厘米,体重58公斤会使我处于越南人口分布中百分位数较低的位置。也许是时候去健身房并增加一些体重了。毕竟,如果你不能相信贝叶斯统计的结果,你还能相信什么呢?
全部0条评论

快来发表一下你的评论吧 !

