关于傅里叶变换变换？

关于傅里叶变换变换？

        答：fourier变换是将连续的时间域信号转变到频率域；它可以说是laplace变换的特例，laplace变换是fourier变换的推广，存在条件比fourier变换要宽，是将连续的时间域信号变换到复频率域（整个复平面，而fourier变换此时可看成仅在jΩ轴）；z变换则是连续信号经过理想采样之后的离散信号的laplace变换，再令z=e^sT时的变换结果（T为采样周期），所对应的域为数字复频率域，此时数字频率ω=ΩT。——参考郑君里的《信号与系统》。

2、什么是Laplace变换？答：

（1）求解方程得到简化。且初始条件自动包含在变换式里。

（2）拉氏变换将“微分”变换成“乘法”，“积分”变换成“除法”。即将微分方程变成代数方程。拉氏变换将时域中卷积运算变换成“乘法”运算。

（3）利用系统函数零点、极点分布分析系统的规律。

在经典控制理论中，对控制系统的分析和综合，都是建立在拉普拉斯变换的基础上的。引入拉普拉斯变换的一个主要优点，是可采用传递函数代替微分方程来描述系统的特性。这就为采用直观和简便的图解方法来确定控制系统的整个特性（见信号流程图、动态结构图）、分析控制系统的运动过程（见奈奎斯特稳定判据、根轨迹法），以及综合控制系统的校正装置（见控制系统校正方法）提供了可能性。

现在给你举个例子：我们学控制的时候，比如一个二阶威廉希尔官方网站 RLC系统微分方程是：LC*Uc''+RC*Uc'+Uc=U设想你借这个微分方程多费劲，那么你用laplace变换，微分方程变为LC*s^2*Uc+RCs*Uc+Uc=U然后Uc=U/(LCs^2+RCs+1)然后可以查表直接得出结果（就跟查积分表一样方便），这不比你解微分方程，强多了么！

（第2种说法）拉普拉斯变换提供了一种变换定义域的方法，把定义在时域上的信号（函数）映射到复频域上（要理解这句话，需要了解一下函数空间的概念--我们知道，函数定义了一种“从一个集合的元素到另一个集合的元素”的关系，而两个或以上的函数组合成的集合，就是函数空间，即函数空间也是一个集合；拉普拉斯变换的“定义域”，就是函数空间，可以说，拉普拉斯变换就是一种处理函数的函数。由于拉普拉斯变换定义得相当巧妙，所以它就具有一些奇特的特质），而且，这是一种一一对应的关系（只要给定复频域的收敛域），故只要给定一个时域函数（信号），它就能通过拉普拉斯变换变换到一个复频域信号（不管这个信号是实信号还是复信号），因而，只要我们对这个复频域信号进行处理，也就相当于对时域信号进行处理（例如设f(t)←→F(s),Re[s]>a，则若我们对F(s)进行时延处理，得到信号F(s-z)，Re[s]>a+Re[z],那么就相当于我们给时域函数乘以一个旋转因子e^zt，即f(t)e^zt←→F(s-z),Re[s]>a+Re[z]；只要对F(s-z)进行反变换，就可以得到f(t)e^zt）。

拉普拉斯变换被用于求解微分方程，主要是应用拉普拉斯变换的几个性质，使求解微分方程转变为求解代数方程（因为求解代数方程总比求解微分方程容易得多！而且，（可以很方便地）对求解结果进行拉普拉斯反变换从而得到原微分方程的解）。

我们总可以容易地画出实变函数的图像（绝大多数函数的确如此），但我们难以画出一个复变函数的图象，这也许是拉普拉斯变换比较抽象的原因之一；而另外一个原因，就是拉普拉斯变换中的复频率s没有明确的物理意义。关于特征根和复数，建议提问者再去看看书中的定义，应该不难理解。3、什么是z变换？

4、什么是FFT（快速fourier变换）？答：音频处理里面常用。就是把波形（时域信号）变换到频域，使得用户更好的分析。频域就是类似于“千千静听”的频谱。这个过程叫“离散傅立叶变换”（DFT）。而FFT是DFT的一种高效快速算法。快速傅立叶变换算法的原理是（来自百度百科）：快速傅氏变换（FFT）是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。设x(n)为N项的复数序列，由DFT变换，任一X（m）的计算都需要N次复数乘法和N-1次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，

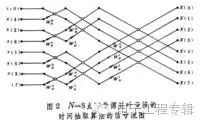
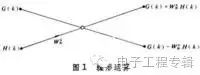
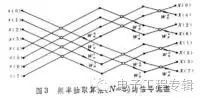
一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出N项复数序列的X（m）,即N点DFT变换大约就需要N2次运算。当N=1024点甚至更多的时候，需要N2=1048576次运算，在FFT中，利用WN的周期性和对称性，把一个N项序列（设N=2k,k为正整数），分为两个N/2项的子序列，每个N/2点DFT变换需要（N/2）2次运算，再用N次运算把两个N/2点的DFT变换组合成一个N点的DFT变换。这样变换以后，总的运算次数就变成N+2（N/2）2=N+N2/2。继续上面的例子，N=1024时，总的运算次数就变成了525312次，节省了大约50%的运算量。而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的DFT运算单元，那么N点的DFT变换就只需要Nlog2N次的运算，N在1024点时，运算量仅有10240次，是先前的直接算法的1%，点数越多，运算量的节约就越大，这就是FFT的优越性。