

V神发布新算法,区块链世界是否进入了新的篇章
区块链
描述
Vitalik近期在其博客上发布了一篇名为《一个99%容错共识的指南》让许多人以为诞生了一个“黑科技”般的新共识算法。然而正如Vitalik自己所说,这一共识算法仍是经典拜占庭将军问题的算法。通过解析,我们可以看到共识算法的研究与创新仍需要遵循CAP等已经被证明过的理论;在此基础上把各类经典分布式算法和加密算法改造应用于区块链领域内,将有可能获得不错的效果。
1、一个新的算法?
Vitalik在其博客上发布了一篇名为《一个99%容错共识的指南》。一时间各大媒体纷纷发布消息称“V神发布的新算法仅需1%节点不作恶”。区块链世界是否一夜之间进入了一个新的篇章?答案可能令人有些沮丧:这并不是一个新研究出来的算法。
事实上,Vitalik在博客中已明确说明“Leslie Lamport在他1982年《拜占庭将军问题》的著名论文里已包含了(增加容错率)的算法,下面我尝试来描述并用一个简化形式来实现它”。他之后也在twitter上强调说明,“我并没有发明出一个可以99%容错的共识协议,而是Leslie Lamport发明的。我只是做了一个解释并把这个算法适应在区块链领域内”。
这究竟是怎么一回事?为弄清楚来龙去脉,我们需要先来讨论共识问题与分布式系统等理论问题。
2、分布式系统理论
实际上在区块链诞生以前,计算机科学就对一致性问题已经有了较多的研究,形成了经过严格证明的分布式系统理论。其中较为经典的理论包括FLP和CAP等。
FLP不可能性原理为:“在网络可靠,存在节点失效(即便只有一个)的最小化异步模型系统中,不存在一个可以解决一致性问题的确定性算法。“即一致性问题的理论下限是无解的。异步分布式系统中不存在一个任意场景下都能实现的共识算法。
CAP原理称为CAP不可能三角,即一致性(Consistency)、可用性(Availablity)和分区容忍性(Partition)三者无法同时满足,需要弱化某个特性来设计分布式系统。所以在FLP不可能性原理前提下,CAP原理为工程实践提供了理论指导。
比CAP更一般的,分布式系统理论中还有对于网络环境特性的定义:包括安全性(Safety)、活性(Liveness)、通讯不可靠性(Unreliable)。通过这些特性我们可以对CAP进行更为一般和直观的定义:

由此可见,一般来说网络分区容忍性P并不是一个可选项,而是必须要在算法中去考虑的因素。这也是为什么分布式系统一般都会在安全性(Safety)和可用性(Liveness)之间进行权衡。
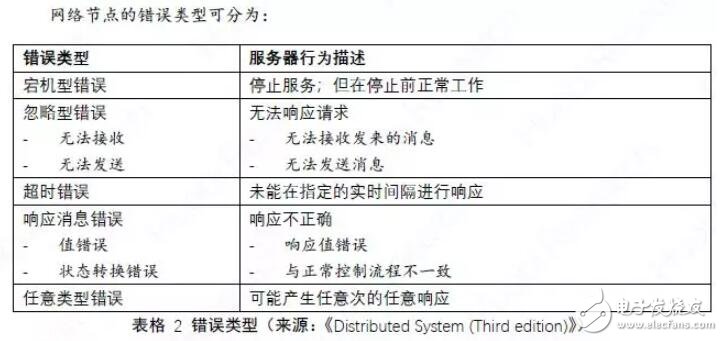
其中,最后一个任意类型的错误是最为严重和棘手的。在这种任意类型错误都可能发生的场景中,服务器有可能产生原本不应该输出的内容,系统要做好最坏情况的准备。例如,当一个服务器向不同的服务器发送截然相反的消息时。这种类型错误,就是拜占庭错误,最早由Pease和Lamport等在上世纪80年代初通过拜占庭将军问题进行描述和分析。
因此相较于分布式数据库,区块链的对于一致性问题的设计和实现要更为复杂,这也是为什么区块链不只是一个简单的分布式数据库的原因之一。
3、 拜占庭将军问题的经典解法
关于BFT问题本身的描述,本文不再赘述。而Lamport等人在其经典论文中除了提出拜占庭将军问题外,也提供了两种解决办法。
第一种为“口头消息”的OM(m)协议,即除了链路上可使用加密安全保障外,不允许使用任何的加密算法。该协议需要两两之间递归的传递大量消息,因此消息复杂度很高,为指数级,不太具有可实际操作性。但这一算法仍有其很高的价值,首先是为“实用拜占庭容错”(Practical Byzantine Fault Tolerance)这一多项式级别复杂度协议的诞生做了一个铺垫;另外,其1/3容错节点数量也被证明为是该类算法的理论上限。
而第二种为“加密消息”的SM(m)协议。该算法与第一种不同之处在于使用签名算法。每个节点都能产生一个不可伪造的签名,并可由其他节点进行验证。当收到消息后,节点会通过签名来判断及验证该消息是否已收到过。最终不再收到消息后,消息共识结束。
该论文已证明该第二种算法可对任意多个节点实现容错(当然网络中至少还应包括2个正常节点,否则无意义)。具体过程可参考论文原文。
然而这一算法也存在其局限性:与许多拜占庭算法在一个异步或者半同步网络环境的假设不同,它假设是在一个“同步”网络内进行,忽略网络节点间通讯延迟;另外,签名身份体系信息需要在网络运行前确定,较难实现扩展。因此,根据CAP理论可以说,这种方式是在不考虑对网络分区(P)等情况容忍的情况下,实现一个很高的一致性(C)与可用性(A)。
4、“99%容错共识算法”及对比分析
作为对比,我们再继续来看一下Vitalik所说的“由Lamport发明而自己进行了描述与简化实现”的共识算法(以下简称“实现版本”;Lamport论文中的版本成为“原版本”)。
该实现版本仍然保留了原有的数字签名体系,即每个节点都能产生一个不可伪造的签名,并可由其他节点进行验证。
与原版本不同的是,为了实现节点间的消息传递,实现版本的算法指定了消息的超时时间,即节点接收到一个消息后,对于消息的检查除了查看签名是否已收到过并且在集合当中以外,还要检查收到消息的时间不应晚于签名对应的时间节点。
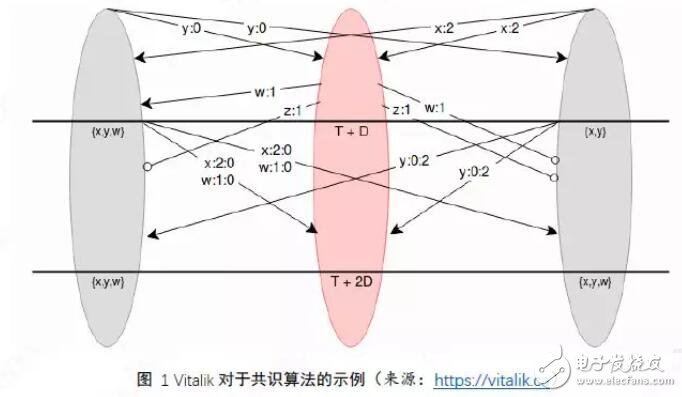
在经过确定好的时间(根据轮次计算得出)后,节点将停止监听,并按照某种确定好的规则来从检查合法的消息中选择一个值来作为共识的结果。
我们对比即可发现,两种算法并没有太本质上的不同,其算法本质都是需要基于签名体系进行。而Vitalik实现版本的共识算法增加的延迟时间要求。这一设计实现在共识协议的具体编写实现时会经常遇到,可确定消息的传播轮次、确保消息传播可在一个指定的时间内结束。
另外,实现版本还讨论了观察者(Observer)作为一个独立角色在网络中传递消息。观察者作为网络中一个被动查看的角色,可接收、检查消息并直接转发(不签名)给其他节点。这需要对观察者引入一个不一样的延迟时间,以解决恶意节点故意给观察者晚发消息使得正常消息超时的问题。
5、应用及启发
正如上述讨论的那样,该类共识方法的主要问题在于对于网络的同步要求较高、可扩展性较差。另外一个实现版本的缺点在于消息量也较大(需要进行N-1轮的N个节点向其他N-1个节点发消息的过程,即消息复杂度为),所以在实际场景中,该类共识方法较难直接应用。
为了更能适用于区块链领域,Vitalik在其文章中也提到该方法可以与目前的其他共识算法(例如PBFT、PoS等)进行结合,例如可间隔一些特定时间运行该算法采用上述讨论的观察者模式随机选择出一些节点运行上述共识进行检查。但如果在两种共识算法相关前提假设都不能满足的情况下,那么共识算法也将失效,即这种改进优化并不能违背原有理论体系。
不过,我们仍可获得不少启发:充分挖掘分布式系统领域的经典理论,并将其改造为适用于区块链领域的共识算法可获得出人意料的效果。例如,PBFT与中本聪类共识结合、Vitalik提出的BFT论文中的SM(m)算法与现有区块链共识结合等等。
此外,尝试应用安全领域内的各种加密算法也可能会获得不错的效果。例如,ByzCoin等也在尝试使用聚合签名等加密算法来对共识机制进行优化改造,可大幅度降低通讯复杂度。
6. 总结
共识算法的研究与创新仍需要遵循CAP等已经被证明过的理论。
在这些理论基础上,可将计算机分布式理论中各类经典算法、安全领域内的各种加密算法加以适应性改造,以应用于区块链领域内,将有可能获得不错的效果。
- 相关推荐
- 区块链
-
什么是区块链 区块链有什么用2018-03-26 0
-
SHA在区块链中的应用2018-03-30 0
-
区块链不是泡沫 马云或将创造新的神话2018-05-18 0
-
区块链行业发展,金融领域应用方向?2018-08-06 0
-
2018区块链技术应用大会:FEC夯实区块链技术,赋能数字经济2018-08-20 0
-
看好区块链的原因2018-08-31 0
-
GeekWallet SDK助力区块链技术在行业中实际应用2018-11-16 0
-
区块链软件:区块链可以对金融机构的商业模式带来什么改变呢?2018-11-19 0
-
区块链软件开发公司谈区块链在供应链金融场景中的应用2018-11-21 0
-
区块链软件开发公司谈未来区块链的主要应用方向2018-11-22 0
-
区块链+教育,是改革的良性循环?2018-12-20 0
-
区块链应用涉及到哪些算法?2019-03-27 0
-
区块链对我们的生活有什么影响2019-07-10 0
-
《区块链+从全球50个案例看区块链的应用与未来》高清pdf2020-03-13 0
-
什么是区块链?区块链都有哪些应用?2021-06-28 0
全部0条评论

快来发表一下你的评论吧 !

