为何基于决策树的模型经久不衰?何时使用基于决策树的模型?

编者按：保险业数据科学家Alan Marazzi用R语言展示了基于决策树的模型的强大和简洁之处。

这是一篇基于决策树的模型的简明介绍，尽量使用非技术术语，同时也给出了模型的R语言实现。由于这篇文章已经够长了，因此我们省略了一些代码。不过别担心，你可以在配套的GitHub仓库中找到完整代码：https://github.com/alanmarazzi/trees-forest

为何基于决策树的模型经久不衰

决策树是一组通常用于分类的机器学习算法。因为它们简单有效，所以也是初学者首先学习的算法之一。你大概很难在最新的机器学习论文和研究上看到它们，但在真实世界项目中，基于决策树的模型仍被广泛使用。

之所以得到如此广泛的使用，主要原因之一是它们的简单性和可解释性。下面是一棵预测天气是否多云的简单决策树。

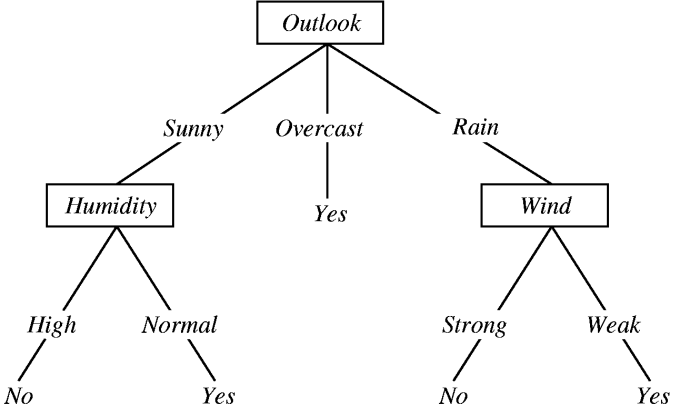
这一方法让我们可以通过传入数据预测某个变量，不过，大概更重要的是我们可以推断预测因子之间的关系。这意味着我们可以从底部开始，看看哪些因素导致了多云。

比如，如果风很小，看起来要下雨了，那说明是多云。对简单模型而言，这些规则可以被人类所学习和应用，或者我们可以生成一份清单以辅助决策过程。通过可视化决策树，我们可以理解机器是如何工作的，为何将某些日子分类为多云，将另一些日子分类为非多云。

尽管这看起来挺微不足道的，但在许多情形下，我们需要知道模型为何做出某些预测。考虑一个预测是否接受胸痛患者的模型。在测试了许多高级模型之后，医生想要搞清楚算法为什么让某些处以危险之中的患者回家。所以他们在数据上运行了一个基于决策树的模型，结果发现算法认为患有哮喘的胸痛病人风险很小。

这是一个巨大的错误。医生非常清楚哮喘和胸痛必须立刻治疗，这意味着哮喘和胸痛的病人会马上得到收治。你发现问题所在了吧？用于建模的数据认为这类病人风险很小，是因为所有这类病人都得到了治疗，所以极少有人在此之后死亡。

何时使用基于决策树的模型

如前所述，当可解释性很重要时，决策树非常好，即使它可能仅用于理解预测哪里出错了。实际上，基于决策树的模型可以变得非常复杂，在损失可解释性的同时，增加准确性。这里存在着一个权衡。

另一个使用决策树的理由是它们非常容易理解和解释。在有一些强预测因子的情形下，决策树可以用来创建可以同时为机器和人类使用的模型。我刚想到的一个例子是预测顾客是否最终会购买某物的决策树模型。

评测也是这些方法大放异彩之处：你很快会发现，用于分类时，即使是相当简单的基于决策树的模型，也很难被大幅超过。我个人经常在要处理的数据集上运行随机森林（后文会介绍这一算法），接着尝试战胜它。

R语言配置

在开始之前，你可能需要先配置一下R环境。

安装如下包：

trees_packages <- c("FFTrees",    "evtree",    "party",    "randomForest",    "intubate",    "dplyr")install.packages(trees_packages)

这些是在R语言中使用基于决策树的模型和数据处理的主要包，但它们不是唯一的。任何你打算使用的基于决策树的模型，几乎都有几十个包可以用，不信的话可以上Crantastic搜索一番。

现在是植树时刻！我决定使用Titanic数据集，机器学习社区最著名的数据集之一。你可以从Kaggle（c/titanic）或GitHub（alanmarazzi/trees-forest）获取这一数据集。我将直接从清洗数据和建模开始讲起，如果你在数据下载、加载上需要帮助，或者缺乏头绪，可以参考我之前的文章Data Science in Minutes或者GitHub仓库中的完整代码。

预备数据

首先，我们看下要处理的数据是什么样子的：

我真心不喜欢有大写字母姓名的数据集，很幸运，我们可以用tolower()函数，一行代码转换为小写字母：

names(titanic) <- tolower(names(titanic))

接着，将sex和embarked变量转换为因子（类别变量）：

titanic$sex <- as.factor(titanic$sex)titanic$embarked <- as.factor(titanic$embarked)

建模时最重要的步骤之一是处理缺失值（NA）。许多R模型可以自动处理缺失值，但大多数只不过是直接移除包含缺失值的观测。这意味着可供模型学习的训练数据变少了，这几乎一定会导致准确率下降。

有各种填充NA的技术：填充均值、中位数、众数，或使用一个模型预测它们的值。我们的例子将使用线性回归替换数据集中年龄变量的缺失值。

乍看起来这个想法有点吓人，有点怪异，你可能会想：“你说的是，为了改进我的模型，我应该使用另一个模型？！”但其实并没有看起来这么难，特别是如果我们使用线性回归的话。

首先让我们看下年龄变量中有多少NA：

mean(is.na(titanic$age))[1] 0.1986532

将近20%的乘客没有年龄记录，这意味着如果我们不替换缺失值，直接在数据集上运行模型的话，我们的训练数据只有714项，而不是891项。

是时候在数据上跑下线性回归了：

age_prediction <- lm(age ~ survived + pclass + fare, data = titanic)summary(age_prediction)

我们干了什么？我们告诉R求解如下线性等式，找出恰当的α、βn的值。

age = α + β1∗survived + β2∗pclass + β3∗fare

然后我们在创建的模型上调用summary()函数，查看线性回归的结果。R会给出一些统计数据，我们需要查看这些数据以了解数据的情况：

Call:lm(formula = age ~ survived + pclass + fare, data = titanic)Residuals:    Min      1Q  Median      3Q     Max -37.457  -8.523  -1.128   8.060  47.505 Coefficients:            Estimate Std. Error t value Pr(>|t|)    (Intercept) 54.14124    2.04430  26.484  < 2e-16 ***survived    -6.81709    1.06801  -6.383 3.14e-10 ***pclass      -9.12040    0.72469 -12.585  < 2e-16 ***fare        -0.03671    0.01112  -3.302  0.00101 ** ---Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 13.03 on 710 degrees of freedom  (177 observations deleted due to missingness)Multiple R-squared:  0.1993,    Adjusted R-squared:  0.1959 F-statistic:  58.9 on 3 and 710 DF,  p-value: < 2.2e-16

上面第一行（Call）提示我们是哪个模型产生了这一结果，第二行显示了残差，之后是系数。这里我们可以查看系数的估计值，它们的标准差，t值和p值。之后是一些其他统计数据。我们看到R实际上移除了含NA的数据（177 observations deleted due to missingness）。

现在我们可以使用这个模型来填充NA了。我们使用predict()函数：

titanic$age[is.na(titanic$age)] <- predict(age_prediction,    newdata = titanic[is.na(titanic$age),])

逻辑回归基准

是否幸存这样的二元分类问题，逻辑回归很难战胜。我们将使用逻辑回归预测泰坦尼克幸存者，并将这一结果作为基准。

别担心，在R中进行逻辑回归非常直截了当。我们引入dplyr和intubate库，然后调用glm()函数运行逻辑回归。glm()接受三个参数，predictors为预测因子，例如年龄、舱等，response为结果变量，这里我们传入survived，family指定返回结果的类别，这里我们传入binomial。

library(dplyr) # 数据处理library(intubate) # 建模工作流# btbt_glb是 %>% 版本的glm函数logi <- titanic %>%    select(survived, pclass, sex, age, sibsp) %>%    ntbt_glm(survived ~ ., family = binomial)summary(logi)

下面让我们查看下逻辑回归模型做出的预测：

# 收集训练数据上的预测logi_pred <- predict(logi, type = "response")# 预测值在0和1之间，我们将其转换为`survived`或`not`survivors_logi <- rep(0, nrow(titanic))survivors_logi[logi_pred > .5] <- 1# 这将成为我们的基准table(model = survivors_logi, real = titanic$survived)

上面的混淆矩阵给出了模型在训练数据上的结果：预测572人死亡（0），319人幸存（1）。矩阵的对角线表明，480项和250项预测正确，而预测死亡的92人实际上幸存了，预测幸存的69人实际上未能幸存。

对这样开箱即用的模型而言，82%的预测精确度已经相当不错了。但是我们想在未见数据上测试一下，所以让我们载入测试集，试下模型在测试集上的效果。

test <- read.csv(paste0("https://raw.githubusercontent.com/",    "alanmarazzi/trees-forest/master/data/test.csv"),    stringsAsFactors = FALSE,    na.strings = "")# 和训练集一样，清洗下数据names(test) <- tolower(names(test))test$sex <- as.factor(test$sex)

下面在测试数据上预测幸存率：

test_logi_pred <- predict(logi, test, type = "response")surv_test_logi <- data.frame(PassengerId = test$passengerid,    Survived = rep(0, nrow(test)))surv_test_logi$Survived[test_logi_pred > .5] <- 1write.csv(surv_test_logi, "results/logi.csv", row.names = FALSE)

我们将结果保存为csv，因为测试数据没有标签，我们并不知道预测是否正确。我们需要将结果上传到Kaggle以查看结果。最终模型做出了77.5%的正确预测。

快速和低成本决策树

终于可以开始植树了！我们将尝试的第一个模型是快速和低成本决策树。这基本上是最简单的模型。我们将使用R的FFTrees包。

# 临时复制下数据集，因为FFTrees包里也包含titanic变量titanicc <- titaniclibrary(FFTrees)titanic <- titaniccrm(titanicc)

载入包，我们只需在选中的变量上应用FFTrees。

fftitanic <- titanic %>%    select(age, pclass, sex, sibsp, fare, survived) %>%    ntbt(FFTrees, survived ~ .)

模型需要跑一会儿，因为要训练和测试不止一棵FFTree。最终得到的结果是一个FFTree对象，包含了所有测试过的FFTree：

fftitanic[1] "An FFTrees object containing 8 trees using 4 predictors {sex,pclass,fare,age}"[1] "FFTrees AUC: (Train = 0.84, Test = --)"[1] "My favorite training tree is #5, here is how it performed:"                        trainn                      891.00p(Correct)               0.79Hit Rate (HR)            0.70False Alarm Rate (FAR)   0.16d-prime                  1.52

我们看到，算法使用最多4个预测因子测试了8棵树，表现最佳的是5号树。接着我们看到了这棵树的一些统计数据。这些输出很有帮助，但可视化方法能够更好地帮助我们理解发生了什么：

plot(fftitanic,     main = "Titanic", decision.names = c("Not Survived", "Survived"))

这一张图中有大量信息，从上往下依次为：观测数目、分类数目、决策树、诊断数据。让我们重点关注决策树。

决策树的第一个节点考虑sex变量：如果是女性（sex != male），我们将直接退出决策树，预测幸存。粗暴，但相当有效。如果是男性，将通过第二个节点pclass。这里，如果是三等舱，我们将退出决策树，预测死亡。接着，如果船费超过£ 26.96（fare），预测幸存。最后一个节点考虑的是age（年龄）：如果年龄大于21.35岁，预测死亡。

在图表的Performance（表现）区域，我们最关心左侧的混淆矩阵，我们可以对比之前逻辑回归得到的混淆矩阵。

此外，我们也可以查看下右侧的ROC曲线。FFTrees包在数据上自动运行逻辑回归和CART（另一种基于决策树的模型），以供比较。仔细看图，我们看到，代表逻辑回归的圆圈基本上完全被5号树的圆圈盖住了，意味着这两个模型表现相当。

现在我们分类测试数据，并提交结果至Kaggle。如同我之前说过的那样，这些决策树极为简单。我上面解释决策树如何工作时，解释每一个节点的句子中都有“如果”，这意味着我们可以依照同样的结构创建一个基于清单的分类器，或者，我们甚至可以记住这些规则，然后手工分类。

ffpred <- ifelse(test$sex != "male", 1,                 ifelse(test$pclass > 2, 0,                        ifelse(test$fare < 26.96, 0,                               ifelse(test$age >= 21.36, 0, 1))))ffpred[is.na(ffpred)] <- 0

只需4个嵌套的ifelse语句，我们就可以分类整个数据集。我们只有2个NA，所以我决定将它们分类为“未幸存”。接着我们只需将csv格式的结果上传到Kaggle，看看模型表现如何。

我们的4个if-else语句表现只比基准差了1%. 考虑到模型的简单性，这是非常出色的成绩。

聚会时分

party包使用条件推理树，比FFTrees更复杂的决策树。简单来说，条件推理树在决定分割节点时，不仅考虑重要性，还考虑数据分布。虽然条件推理树更复杂，但使用起来很简单，加载包后只需使用ctree函数即可创建决策树。

library(party)partyTitanic <- titanic %>%    select(age, pclass, sex, sibsp, fare, survived) %>%    ntbt(ctree, as.factor(survived) ~ .)

运行模型后，我们可以调用这个包的绘图函数可视化得到的决策树，plot(ctree_relust)。这里我们不在乎其他花里胡哨的东西，只在意最终得到的决策树。所以会使用一些可选参数让输出整洁一点。

plot(partyTitanic, main = "Titanic prediction", type = "simple",     inner_panel = node_inner(partyTitanic,                              pval = FALSE),     terminal_panel = node_terminal(partyTitanic,                                    abbreviate = TRUE,                                    digits = 1,                                    fill = "white"))

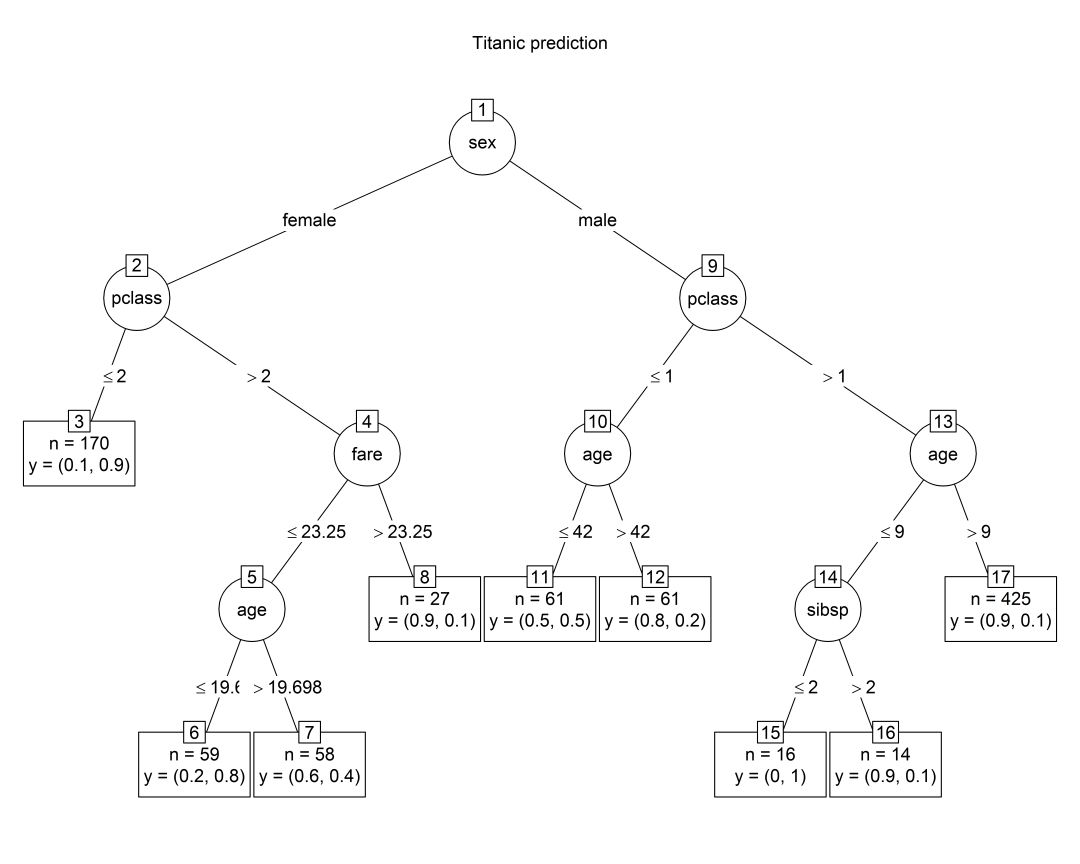
不幸的是较大的树占用更多空间，如果再加上一些节点，图就基本上看不清了。将这棵树和上面那棵FFTree比较一下，我们看到现在这棵树更复杂：之前我们直接预测每个男性死亡，现在这个模型尝试将男性分为多种情况。

增加的复杂性降低了15%的训练误差。和上面的FFTree相比，这是一项改进。

train_party <- Predict(partyTitanic)table(tree = train_party, real = titanic$survived)

不过，很遗憾，我们下面将学到机器学习最重要的一课。事实上，在测试集上的分类正确率只有73.7%！

你也许会问，这怎么可能？我们刚看到的是过拟合现象。模型考虑的一些变量最终看来其实是噪声。结果在训练集上改善了，但在未见数据上的表现变差了。有多种应对这一问题的方式，比如剪枝。剪枝的意思是削减分支，比如通过降低树的最大深度达成。剪枝搭配交叉验证，很可能改善测试数据上的结果。

集成模型

目前为止，我们开发的都是单个学习者，意味着我们通过一个模型找到解决方案。另一系列的机器学习算法是集成，通过许多所谓的弱小学习者创建的模型。背后的理论是通过使用许多学习者（在我们的例子中是决策树），结合他们的选择，我们能得到良好的结果。

集成模型因模型创建方法、组合结果方式的不同而不同。可能看起来有点杂乱，但部分集成方法通常是开箱即用的，是一个很好的优化结果的选择。

集成的目的是为了减少方差。比如，我们上面在训练集上得到了良好的结果，但在测试集上的误差率却很大。如果我们有不同的训练集，不同的模型，那么各自会有不同的偏差，集成之后就能得到更好的结果。

我们将查看三种不同的集成算法：Bagging、随机森林、Boosting。

Bagging

bagging的主要思路相当简单：如果我们在不同的训练集上训练许多较大的决策树，我们将得到许多高方差、低偏差的模型。平均每棵树的预测，我们就能得到方差和偏差相对较低的分类。

你可能已经发现一个问题，我们并没有许多训练集。为了应对这一问题，我们通过bootstrap方法创建这些训练集。bootstrap不过是一种有放回的重复取样方法。

x <- rnorm(100) # 生成随机向量# 定义固定取样函数boot_x <- function(x, size) {    sample(x, size, replace = TRUE)}# 循环取样，直到取满需要的样本bootstrapping <- function(x, reps, size) {    y <- list()    for (i in seq_len(reps)) {        y[[i]] <- boot_x(x, size)    }    y}# 结果是一个列表z <- bootstrapping(x, 500, 20)

为了在泰坦尼克数据上运行bagging，我们可以使用randomForest包。这是因为bagging和随机森林差不多，唯一的区别是在创建决策树时考虑多少预测因子。bagging中，我们考虑数据集中的每个预测因子，我们可以通过设置mtry参数做到这一点。

library(randomForest)# 如果你希望重现结果，别忘了设置一样的随机数种子set.seed(123)# 创建bagging模型titanic_bag <- titanic %>%    select(survived, age, pclass, sex, sibsp, fare, parch) %>%    ntbt_randomForest(as.factor(survived) ~ ., mtry = 6)

注意，这里我们将survived作为因子（as.factor）传入，这样就可以使函数创建分类树，而不是回归树（是的，决策树同样可以用于回归）。

bagging默认创建500棵树，如果你想要增加更多树，可以传入ntree参数，设定一个更高的数值。

上面的代码有一个问题，直接跳过NA，不作预测。为了在避免进一步特征工程的前提下，生成符合Kaggle要求的结果，我决定将测试集中的NA用中位数替换。不幸的是，这个问题限制了预测能力，结果是66.5%的正确预测率。

随机森林

随机森林是最著名的机器学习算法之一，原因是它开箱即用的效果好到没道理。随机森林几乎和bagging一样，只不过使用较弱的学习者，创建决策树时只考虑有限数量的预测因子。

你可能会问使用全部预测因子和仅使用部分预测因子有什么区别。答案是使用所有预测因子时，在不同的bootstrap取样的数据集上创建决策树时，前两个分割很可能是一样的，因为创建决策树时考虑的是预测因子的重要性。所以使用bagging创建的500棵树会很相似，相应地，做出的预测也会很相似。

为了限制这一行为，我们使用随机森林，通过mtry参数限制预测因子。我们使用交叉验证决定“最好”的参数值，或者尝试一些经验法则，比如ncol(data)/3和sqrt(ncol(data))，不过在这个例子中我将mtry参数值定为3.

我建议你试验不同的值，然后查看发生了什么，以更好地理解随机森林算法。

set.seed(456)titanic_rf <- titanic %>%    select(survived, age, pclass, sex, sibsp, fare, parch) %>%    ntbt_randomForest(as.factor(survived) ~ ., mtry = 3, n.trees = 5000)

结果是74.6%，比bagging要好不少（译者注：这里的比较不是很公平，因为之前bagging只用了500棵树，而这里随机森林用了5000棵树，感兴趣的读者可以试下统一数量后再做比较），但还是比逻辑回归差一点。

随机森然有很多实现，也许我们可以尝试下party包，用下条件推断树构成的随机森林。

set.seed(415)titanic_rf_party <- titanic %>%    select(survived, age, pclass, sex, sibsp, fare, parch) %>%    ntbt(cforest, as.factor(survived) ~ .,            controls = cforest_unbiased(ntree = 5000, mtry = 3))

如你所见，代码和之前差不多，但是结果是不是差不多呢？

这个结果差不多可以算是和逻辑回归打了个平手。

Boosting

和之前“奋发”学习的算法不同，boosting缓慢学习。实际上，为了避免过拟合，bagging和随机森林需要创建几千棵决策树，然后平均所有预测。boosting的方式与此不同：创建一棵树，结果基于第一棵树的结果创建另一棵树，以此类推。

boosting比其他基于决策树的算法学得慢，这有助于防止过拟合，但也要求我们小心地调整学习速度。从下面的代码中，我们能看到，boosting的参数和随机森林比较相似。

library(gbm)set.seed(999)titanic_boost <- titanic %>%    select(survived, age, pclass, sex, sibsp, fare, parch) %>%    ntbt(gbm, survived ~ .,         distribution = "bernoulli",         n.trees = 5000,         interaction.depth = 3)

我们使用gbm包中的同名函数（ntbt），并指定distribution参数为bernoulli（伯努利分布），告诉函数这是一个分类问题。n.trees参数指定创建决策树的数目，interaction.depth指定树的最大深度。

76%，和逻辑回归、随机森林、FFTrees的结果差不多。

我们学到了

复杂模型 > 简单模型 == 假。 逻辑回归和FFTrees很难战胜，而且我们只需一点特征工程就可以进一步提升简单模型的表现。

特征工程 > 复杂模型 == 真。 特征工程是一项艺术。它是数据科学家最强大的武器之一，我们可以使用特征工程改进预测。

创建模型 == 乐！ 数据科学家很有意思。尽管R有时会让人有点沮丧，但总体而言学习R回报丰厚。如果你希望进一步了解细节，或者想要一个逐步的指南，你可以访问文章开头提到的GitHub仓库，里面有完整的代码。

如果你喜欢这篇文章，请留言、转发。你也可以订阅我的博客rdisorder.eu