

帮你们破除RL的神秘感,理清各算法发展的脉络
电子说
描述
前言
之前通过线上课程学习David Silver的《强化学习》,留下深刻印象的是其中一堆堆的公式。公式虽然严谨,但是对于我来说,遇到实际问题时,我需要在脑海中浮现出一幅图或一条曲线,帮我快速定位问题。正所谓“一图胜千言”嘛。
最近终于找到了这样一幅图。国外有大神用漫画的形式讲解了强化学习中经典的Advantage-Actor-Critic(A2C)算法。尽管标题中只提及了A2C,实际上是将整个RL的算法思想凝结在区区几幅漫画中。
我很佩服漫画的作者,能够从复杂的公式中提炼出算法的精髓,然后用通俗易懂、深入浅出的方式展示出来。能够将厚书读薄,才能显现出一个人的功力。
有这样NB的神作,不敢独吞,调节一下顺序,补充一些背景知识,加上我自己的批注,分享出来,以飨读者。 原漫画的地址见:Intuitive RL: Intro to Advantage-Actor-Critic (A2C),英语好的同学可以科学上网看原版的。
基本概念
强化学习中最基础的四个概念:Agent, State, Action, Reward

Agent:不用多说,就是你的程序,在这里就是这只狐狸。
Action: agent需要做的动作。在漫画中,就是狐狸在岔路口时,需要决定走其中的哪一条路。
State: 就是agent在决策时所能够掌握的所有信息。对于这只狐狸来说,既包括了决策当时的所见所闻,也包括了它一路走来的记忆。
Reward:选择不同的路,可能遇到鸟蛋(正向收益),也有可能遇到豺狼(负向收益)。
为什么Actor? 为什么Critic?
正如我之前所说的,Actor-Critic是一个混合算法,结合了Policy Gradient(Actor)与Value Function Approximation (Critic)两大类算法的优点。原漫画没有交待,一个agent为什么需要actor与critic两种决策机制。所以,在让狐狸继续探险之前,有必要先简单介绍一下Policy Gradient (策略梯度,简称PG)算法,后面的内容才好理解。
Policy Gradient看起来很高大上,但是如果类比有监督学习中的多分类算法,就很好理解了。两类算法的类比(简化版本)如下表所示,可见两者很相似

“分类有监督学习”与“策略梯度强化学习”的对比
还是以狐狸在三岔路口的选择为例
N就是样本个数
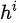 就是每次决策前的信息,即特征
就是每次决策前的信息,即特征
如果选择哪条岔道是有唯一正确答案的,并且被标注了,即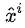 ,则我们可以用“多分类算法”来学习它。
,则我们可以用“多分类算法”来学习它。
但是,在强化学习中,每次选择没有唯一正确的答案,而且每次选择的收益也是延后的。既然我们不知道所谓“唯一正确答案”,我们就做一次选择  (未必是最优的),再将这个选择对最终loss或gradient的贡献乘以一个系数,即上式中的
(未必是最优的),再将这个选择对最终loss或gradient的贡献乘以一个系数,即上式中的 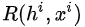 ,有个学术的名字叫“Likelihood Ratio”
,有个学术的名字叫“Likelihood Ratio”
怎么理解Likelihood Ratio这个乘子?这个乘子必须满足什么样的要求?最简单的形式, 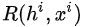 可以是一次实验(如AlphaGo的一次对弈,狐狸一天的探险)下来的总收益。从而PG可以写成如下形式:
可以是一次实验(如AlphaGo的一次对弈,狐狸一天的探险)下来的总收益。从而PG可以写成如下形式:

Policy Gradient公式
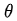 是优化变量
是优化变量
公式左边是平均收益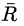
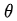
公式右边中,N是总实验的次数,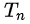
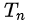
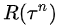 是第n次实验
是第n次实验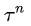
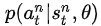 是第n次实验中,第t步时,在当前state是
是第n次实验中,第t步时,在当前state是
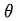 的概率的情况下,选择了动作
的概率的情况下,选择了动作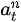
以上公式表明:
如果第n次实验的总收益 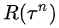 是正的,则
是正的,则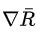

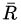 假定第n次实验中的每步决策都是正确的,应该调节
假定第n次实验中的每步决策都是正确的,应该调节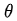
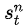

如果第n次实验的总收益 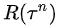 是负的,则
是负的,则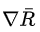
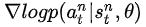
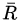 假定第n次实验中的每步决策都是错误的,应该调节
假定第n次实验中的每步决策都是错误的,应该调节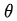
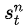
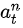
基于“真实有效的决策,在成功实验出现的次数,比在失败实验出现的次数,要多”这样的假设,以上方法还是能够学到东西的。
但是,以上算法中统一用 做乘子,还是太简单粗暴,有些“一荣倶荣,一损俱损”搞“连坐”的味道。因此,在实际算法中,围绕着policy gradient前的那个乘子,衍生出多种变体,
做乘子,还是太简单粗暴,有些“一荣倶荣,一损俱损”搞“连坐”的味道。因此,在实际算法中,围绕着policy gradient前的那个乘子,衍生出多种变体,
比如考虑每步决策的直接收益的时间衰减,就是REINFORCE算法。
如果用V(S),即“状态值”state-value,来表示PG前的系数,并用一个模型来专门学习它,则这个拟合真实(不是最优)V(s)的模型就叫做Critic,而整个算法就是Actor-Critic算法。
因为篇幅所限,简单介绍一下V(s)与Q(s,a)。它们是Value Function Approximation算法中两个重要概念,著名的Deep Q-Network中的Q就来源于Q(s,a)。V(s)表示从状态s走下去能够得到的平均收益。它类似于咱们常说的“势”,如果一个人处于“优势”,无论他接下去怎么走(无论接下去执行怎样的action),哪怕走一两个昏招,也有可能获胜。具体精确的理解,还请感兴趣的同学移步David Silver的课吧。
重新回顾一下算法的脉络,所谓Actor-Critic算法
Actor负责学习在给定state下给各候选action打分。在action空间离散的情况下,就类似于多分类学习。
因为与多分类监督学习不同,每步决策时,不存在唯一正确的action,所以PG前面应该乘以一个系数,即likelihood ratio。如果用V(S),即state-value,来表示PG前的乘子,并用一个模型来专门学习它,则这个拟合V(s)的模型就叫做Critic,类似一个回归模型 。
如果用Critic预测值与真实值之间的误差,作为likelihood ratio,则PG前的乘子就有一个专门的名称,Advantage。这时的算法,就叫做Advantage-Actor-Critic,即A2C。
如果在学习过程中,引入异步、分布式学习,此时的算法叫做Asynchronous-Advantage-Actor-Critic,即著名的A3C。
狐狸的探险
上一节已经说明了狐狸(Agent)为什么需要actor-critic两个决策系统。则狐狸的决策系统可以由下图表示
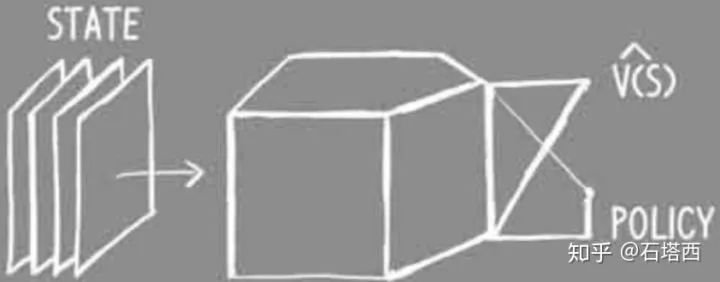
state是狐狸做决策时所拥有的一切信息,包括它的所见所闻,还有它的记忆。
critic负责学习到准确的V(s),负责评估当前状态的“态势”,类似一个回归任务。
actor负责学习某状态下各候选action的概率,类似一个多分类任务。
在第一个路口
狐狸的critic觉得当前态势不错,预计从此走下去,今天能得20分,即V(s)=20
狐狸的actor给三条路A/B/C都打了分
狐狸按照A=0.8, B=C=0.1的概率掷了色子,从而决定走道路A(没有简单地选择概率最大的道路,是为了有更多机会explore)
沿A路走,采到一枚蘑菇,得1分
把自己对state value的估计值,采取的动作,得到的收益都记录下来
在接下来的两个路口,也重复以上过程:
狐狸的反思:更新Critic
毕竟这只狐狸还太年轻,critic对当前状态的估计可能存在误差,actor对岔道的打分也未必准确,因此当有了三次经历后,狐狸停下来做一次反思,更新一下自己的critic和actor。狐狸决定先更新自己的critic。
之前说过了,critic更像是一个“回归”任务,目标是使critic预测出的state value与真实state value越接近越好。以上三次经历的state value的预测值,狐狸已经记在自己的小本上了,那么问题来了,那三个state的真实state value是多少?
在如何获取真实state value的问题上,又分成了两个流派:Monte Carlo(MC)法与Temporal-Difference(TD)法。
MC法,简单来说,就是将一次实验进行到底,实验结束时的V(s)自然为0,然后根据Bellman方程回推实验中每个中间步骤的V(s),如下图所示(图中简化了Bellman方程,忽略了时间衰减)。MC法的缺点,一是更新慢,必须等一次实验结束,才能对critic/actor进行更新;二是因为V(s)是状态s之后能够获得的平均收益,实验越长,在每个步骤之后采取不同action导致的分叉越多,但是MC法仅仅依靠上一次实验所覆盖的单一路径就进行更新,显然导致high variance。
Monte Carlo法
另一种方法,TD法,就是依靠现有的不准确的critic进行bootstrapping,逐步迭代,获得精确的critic
现在狐狸要反思前三个状态的state value,狐狸假定当前critic(老的,尚未更新的)在当前状态(第4个状态)预测出state value是准确的,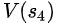 =18
=18
根据V(s)的定义,V(s)代表自s之后能够获得的平均收益,既然 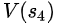
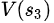 =18+2=20
=18+2=20
同理, 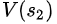 =
=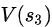 +
+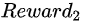 =20+20=40
=20+20=40
同理,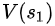 =
= 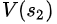 +
+ ==40+1=41
==40+1=41
Temporal-Difference法
如上图中狐狸的记事本所示,对于以上三步,狐狸既有了自己对当时state value的预测值,也有了那三个state value的“真实值”,上面的红字就是二者的差,可以用类似“回归”的方法最小化求解。
狐狸的反思:更新Actor
正如前文所述,critic的作用是为了准确预测Policy Gradient前的那个系数,即Likelihood Ratio。
likelihood ratio>0,应该调节actor的参数,提升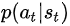 的概率,即鼓励当时采取的动作
的概率,即鼓励当时采取的动作
likelihood ratio<0,应该调节actor的参数,降低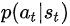 抑制当时采取的动作
抑制当时采取的动作
那么critic应该为PG贡献一个什么样的likelihood ratio呢?考虑以下的例子
在一个三岔路品,狐狸感受到的状态是前路有狼、陷阱和破桥,哪条道都不好走,因此狐狸预测当前“状态值”极差, =-100
=-100
狐狸还是硬着头皮选择了一条稍微好走的路,中间丢失了许多食物,收益=-20
恰好过了桥之后,一天也就结束了,最终状态的 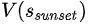 =0。根据critic bootstrapping进行回推,当初过桥前
=0。根据critic bootstrapping进行回推,当初过桥前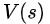 “真实状态值”=-20
“真实状态值”=-20
那么actor中,policy gradient之前的likelihood ratio应该是多少?能不能选择采取动作之后的直接收益,-20? 如果是的话,因为选择过桥,导致狐狸丢了20分,以后狐狸在相同状态下(看见前路有狼、陷阱和破桥)选择“过破桥”的概率应该降低!!!
以上结论显然是不合适的,下次不选桥,难道要选狼与陷阱?!哪里出错了?
换个思路:
当初在岔路口时,狐狸对当时state value的预测是-100,
选择了破桥之后,根据critic bootstrapping推导回去,发现之前在岔路口时的状态还不至于那么差,“真实state value”=-20。
回头来看,选择“破桥”还改善了当时的处境,有80分的提升。
因此,之后在相同状态下(看见前路有狼、陷阱和破桥)选择“破桥”的概率,不仅不应该降低,反而还要提高,以鼓励这种明智的选择,显然更合情合理。
这里,某个状态s下的state value的“真实值”与预测值之间的差异,就叫做Advantage,拿advantage作为Policy Gradient之前的乘子,整个算法就叫做Advantage-Actor-Critic (A2C)。
Advantage
注意state value的“真实值”与预测值之间的差异在Actor与Critic上发挥的不同作用
在Actor中,这个差值就叫做Advantage,用来指导Actor应该鼓励还是抑制已经采取的动作。动作带来的Advantage越大,惊喜越大,下次在相同状态下选择这个动作的概率就应该越大,即得到鼓励。反之亦然。
在Critic中,这个差值就叫做Error,是要优化降低的目标,以使Agent对状态值的估计越来越准确。间接使Actor选择动作时也越来越准确。
其他
A2C的主要思路就这样介绍完毕了。在原漫画中,还简单介绍了A3C、Entropy Loss的思想,就属于旁枝末节,请各位看官们移步原漫画。其实A3C的思路也很简单(实现就是另一回事了),无非是让好几只狐狸并发地做实验,期间它们共享经验教训,以加速学习。
A3C
小结
本篇算是一个半原创吧,在翻译的同时,也增加了我对Actor-Critic的理解。
对于初学RL的同学,希望本文能够帮你们破除RL的神秘感,理清各算法发展的脉络,以后在David Silver课上看到那些公式时,能够有“似曾相识”的感觉。
对于掌握了RL基本算法的同学,也希望你们能够像我一样,当遇到实际问题时,先想到漫画中的小狐狸,定位问题,再去有的放矢地去翻书找公式。
很佩服原漫画的作者,能将复杂的公式、原理用如此通俗易懂、深入浅出的方式讲明白。再次向原作者致敬,Excellent Job !!!
-
集合william hill官网 上的很多msp430压缩为一个压缩包,帮你们省时省力2012-08-11 0
-
洗衣机无感算法疑问?2022-11-10 0
-
魅族X计划神秘开启,重磅新品即将登场2016-10-25 1150
-
vivo高端黑色光影风vivoXplay6照片神秘浮现,质感爆棚!2017-03-18 991
-
改进的RL模糊星图复原算法_杨阳2017-03-19 529
-
人工智能迈入第三波发展 未来将可自动建立脉络2018-01-02 726
-
SpaceX2018年首次发射成功 发射富有神秘感2018-01-08 1754
-
探索神秘而又圈粉无数的商显利器LED透明屏2022-11-17 887
-
紫光展锐分析5G广播技术的发展脉络2024-08-26 582
全部0条评论

快来发表一下你的评论吧 !

