

啥是佩奇排名算法?通过动画来理解进行计算的具体流程
电子说
描述
佩奇排名介绍
佩奇排名是根据页面之间的链接结构计算页面的值的一种算法。下面我们通过动画来理解进行计算的具体流程。
假设一个正方形表示一个 WEB 页面,一个箭头表示一个页面之间的链接。
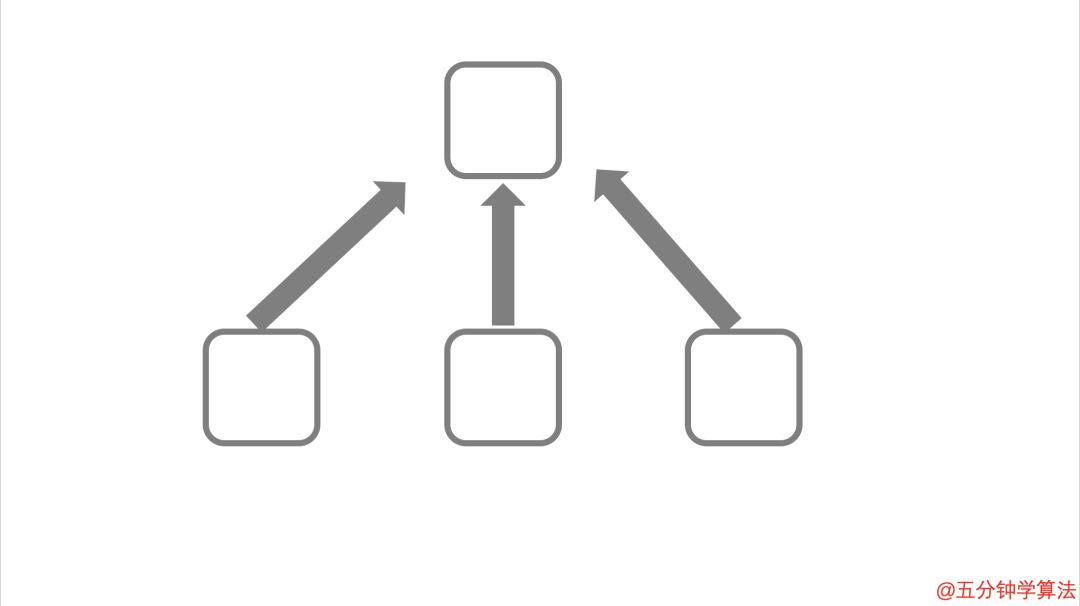
此图表明下面 3 页包含指向上面 1 页的链接
在佩奇排名算法中,网页指向的链接越多,页面被确定为越重要。
因此,在这里,确定英国威廉希尔公司网站 最重要。
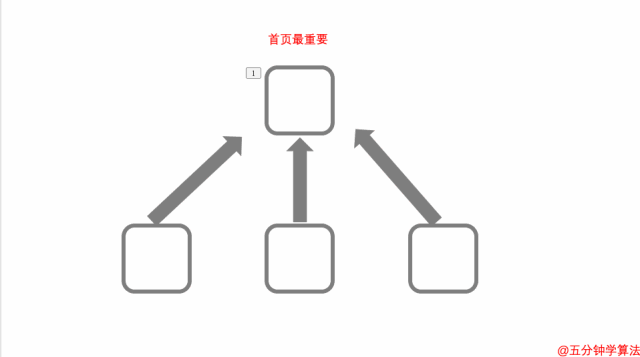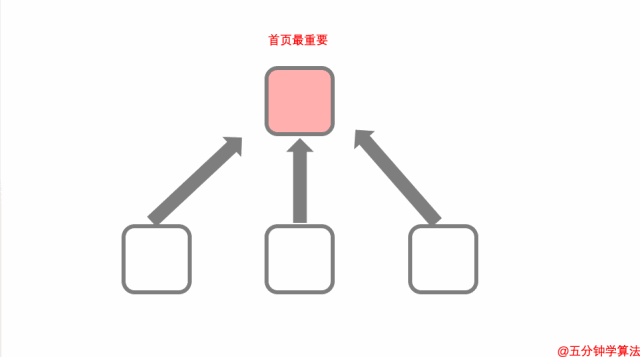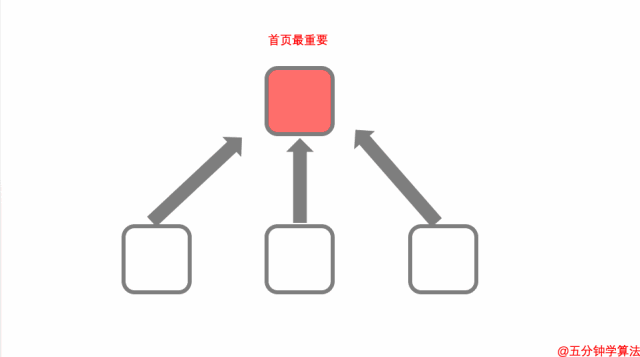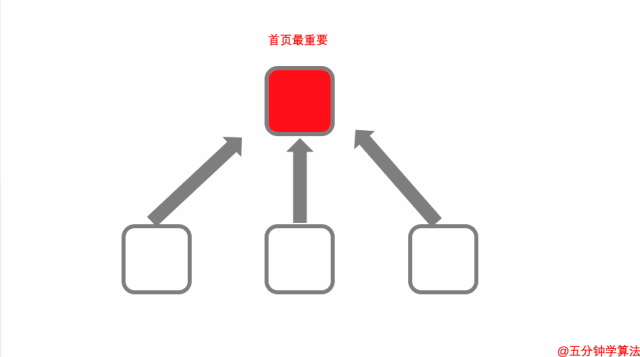
确定英国威廉希尔公司网站 最重要
实际上,每个页面的重要性都是通过计算来量化的。
基本的计算方法思想
1.未链接的页面分数为 1
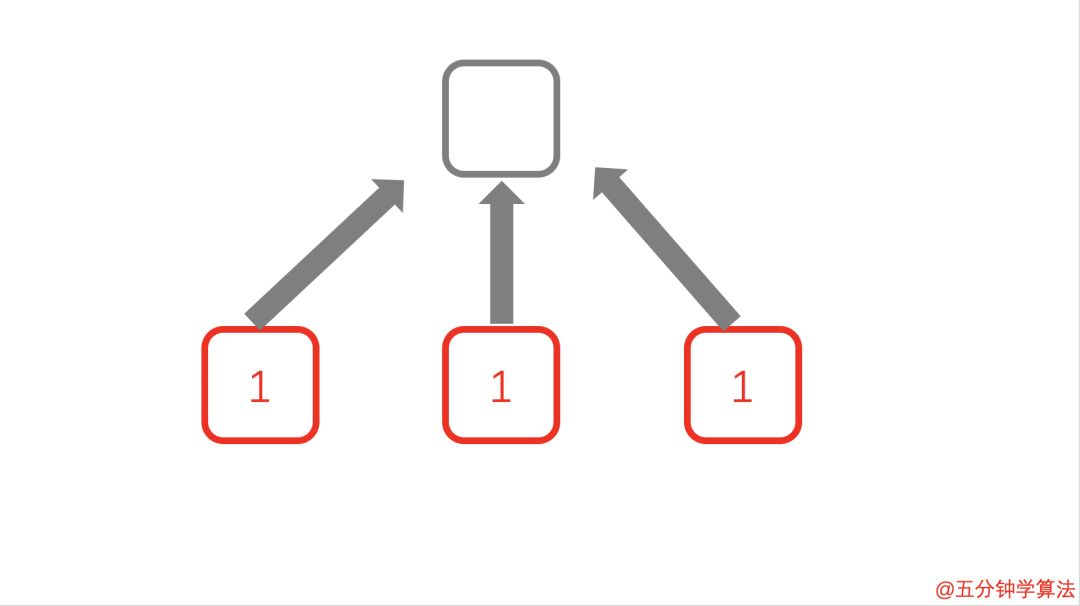
未链接的页面分数为 1
2.有链接的页面得分为正在链接的页面的总得分

有链接的页面得分为正在链接的页面的总得分
3.当有多个网页的链接时,链接分数均匀分布

链接分数均匀分布
4.来自高度链接网页的链接具有很高的价值
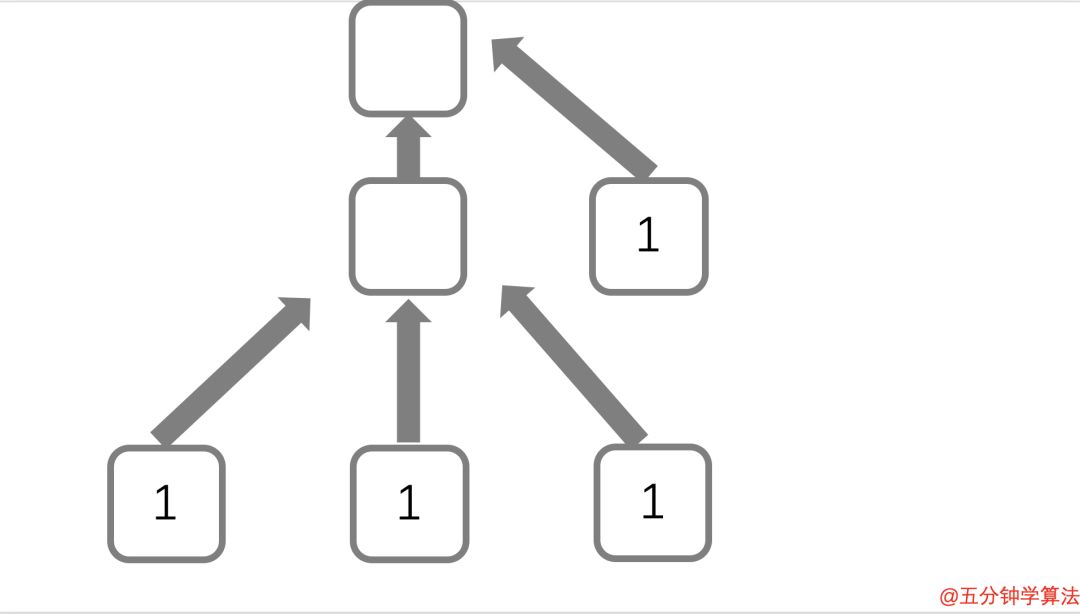
该图中心页面有三个独立页面指向它的链接,所以它的分数是 3 。
英国威廉希尔公司网站 有一个很大的分数,因为链接是从分数为 3 的页面指向它的。
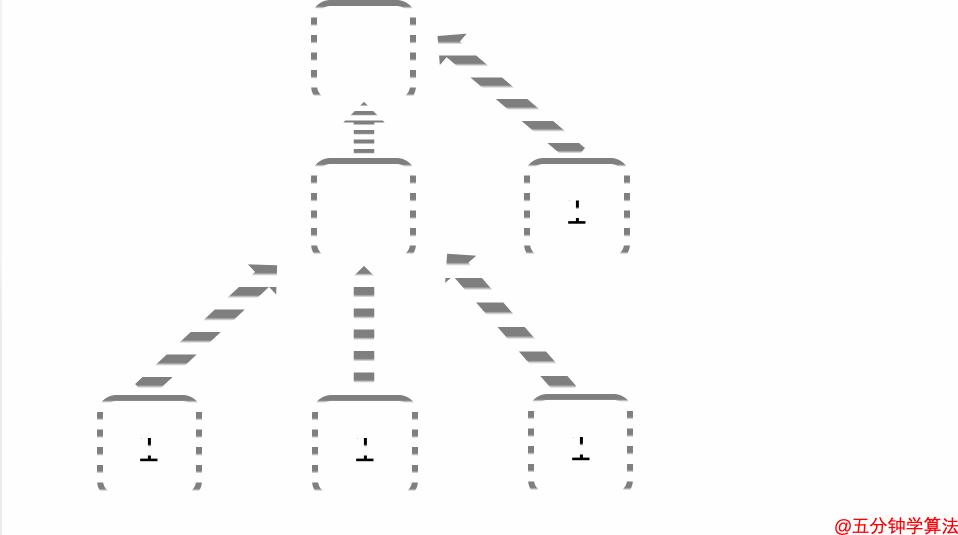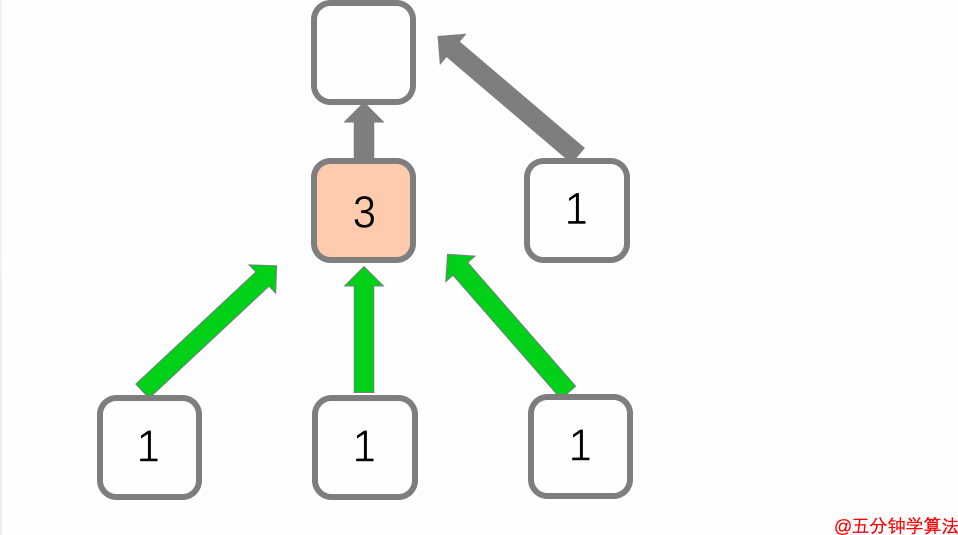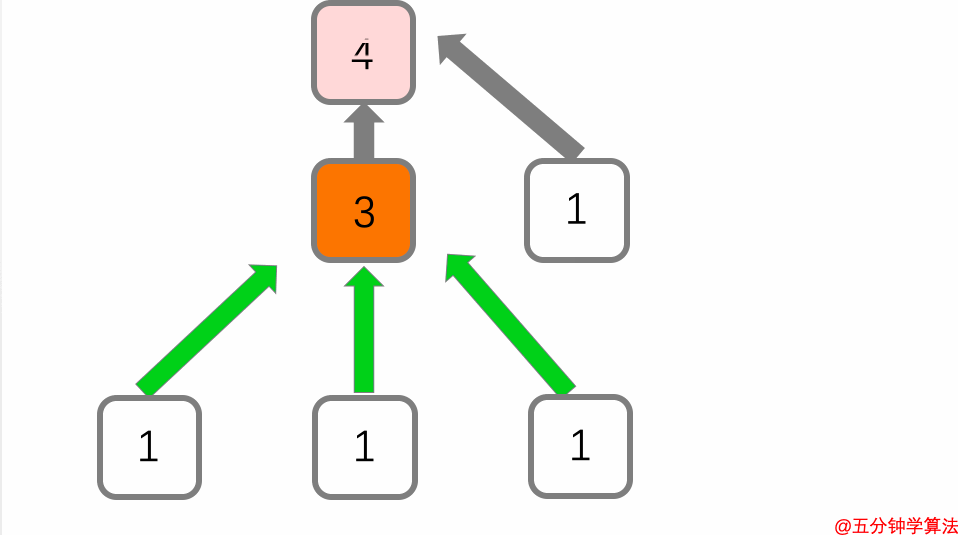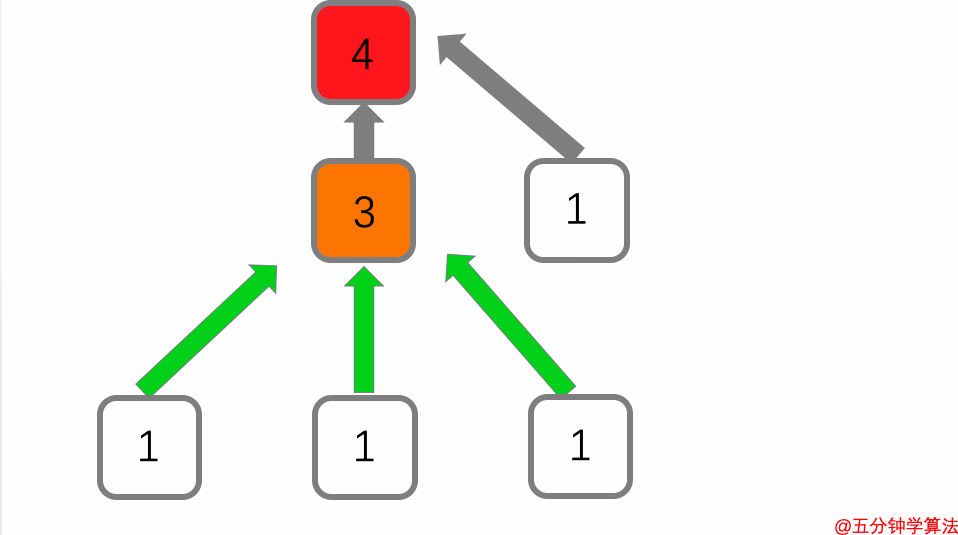
在动画中的六个页面中,判断最上面的页面是最重要的页面----这是佩奇排名的基本思想。
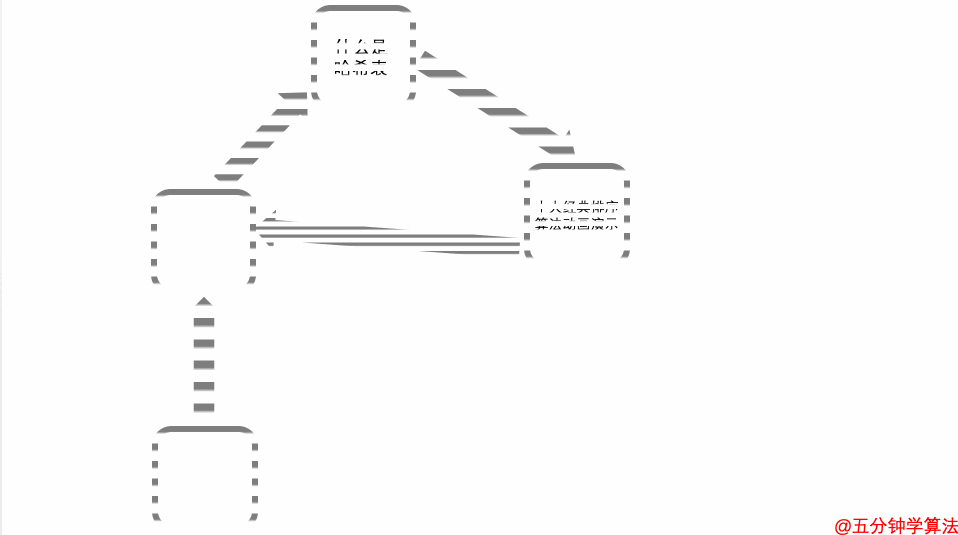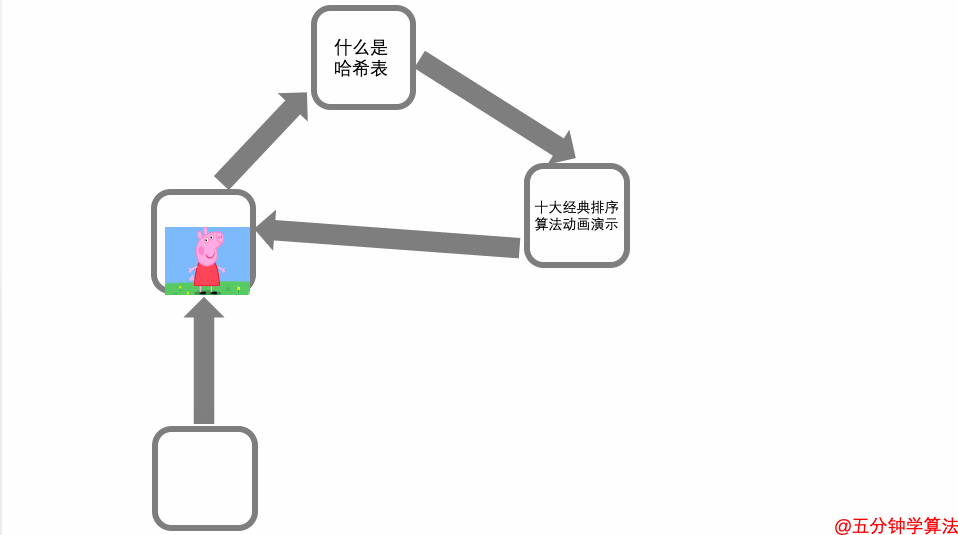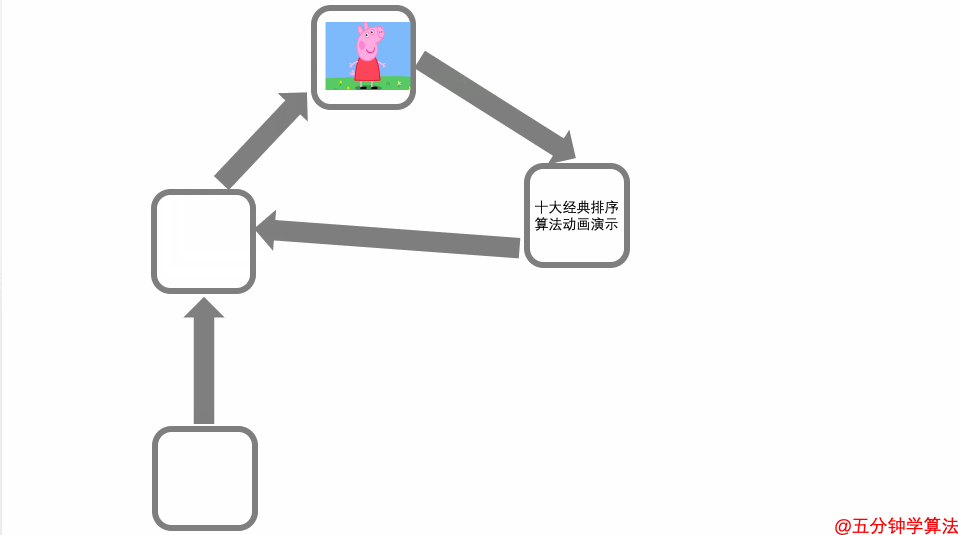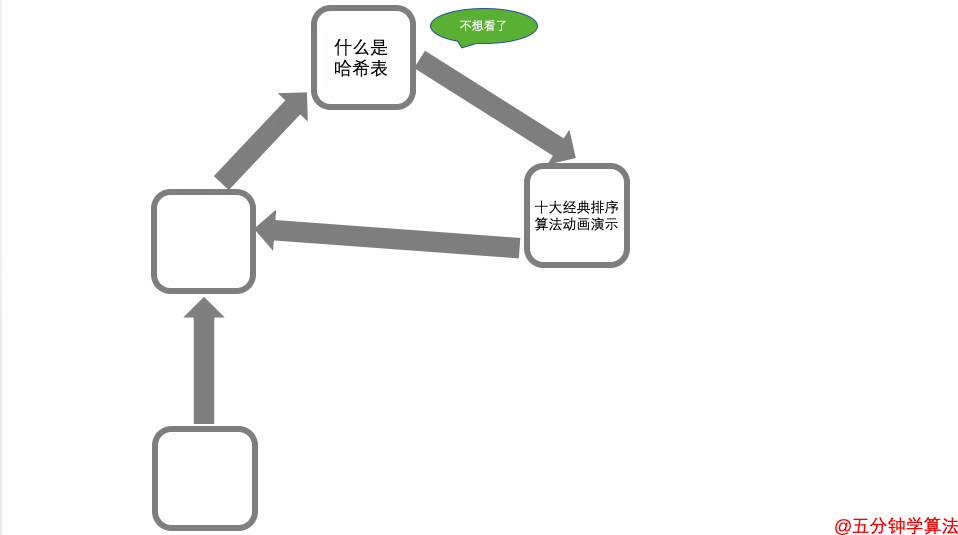
基本的计算方法思想的循环问题

如果按照顺序来计算每个页面的分数时,那么就会出现问题:以这种方式计算,它将无限循环,并且在循环中的页面得分在任何地方都会很高。
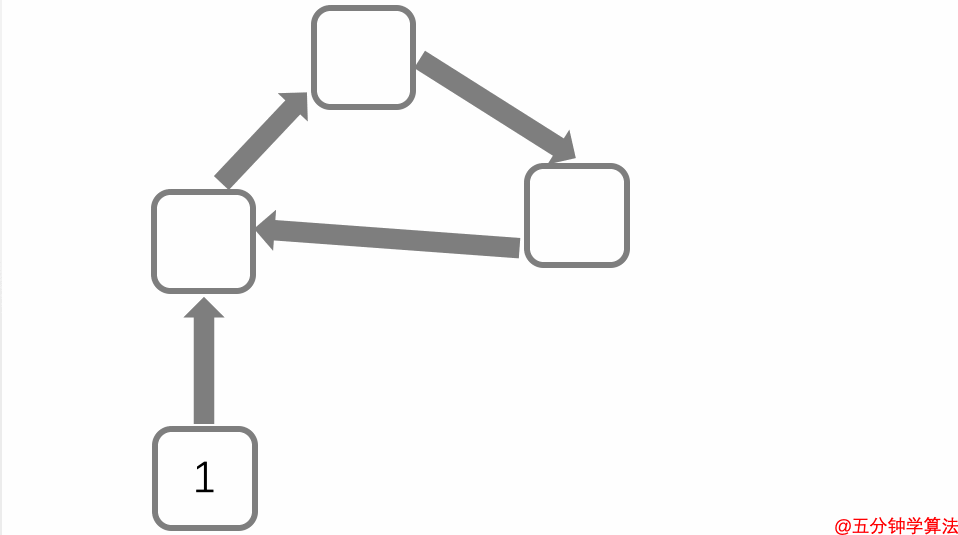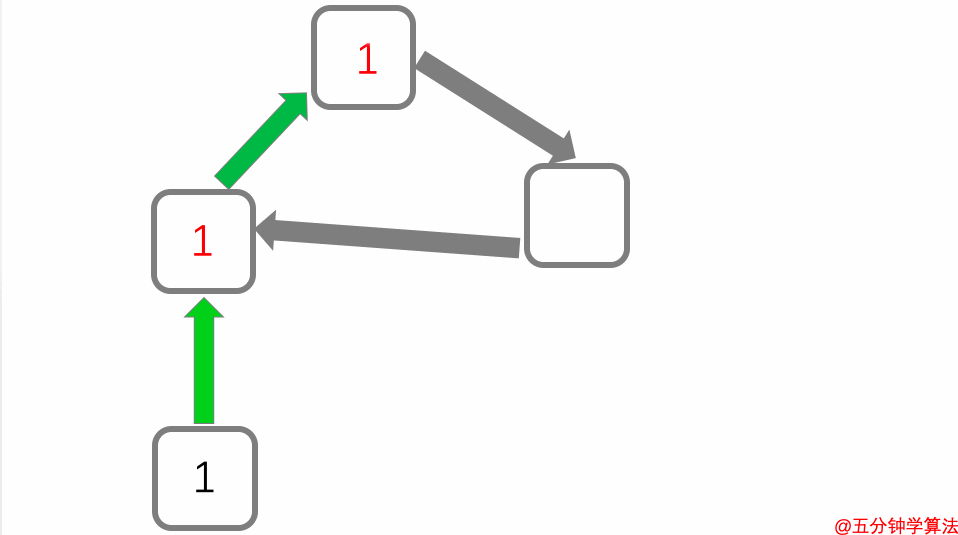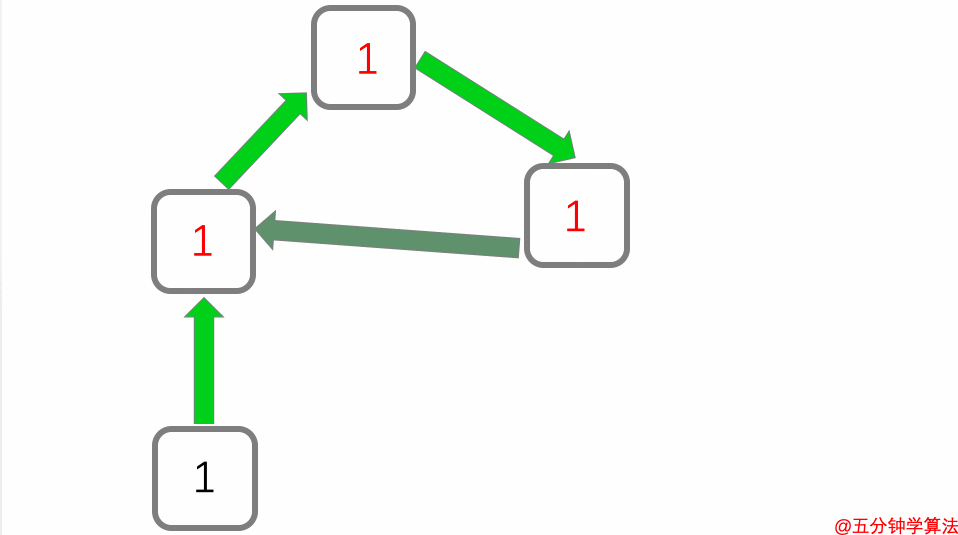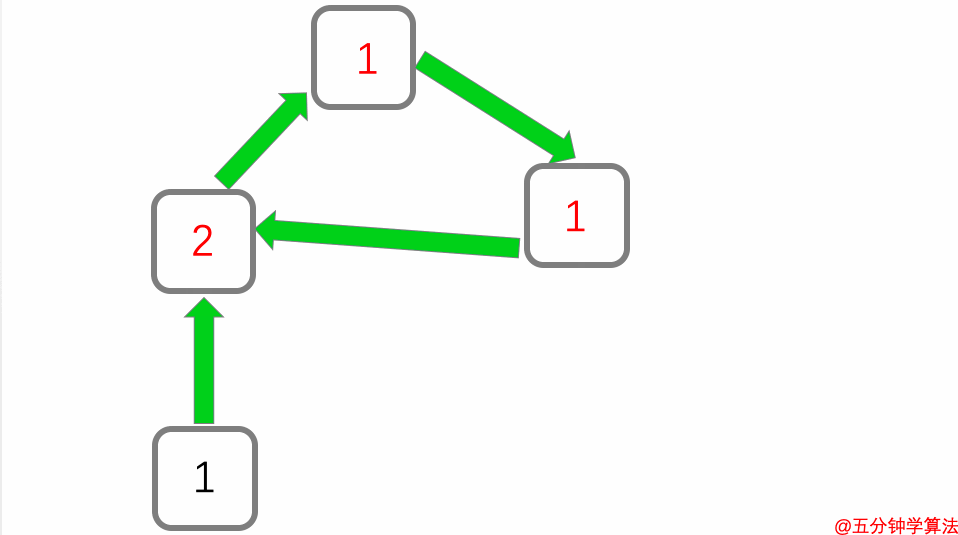
循环的问题可以通过“随机游走模型”的计算方法来解决。
随机游走模型
以小猪佩奇浏览网页为例。
小猪佩奇开始访问「五分钟学算法」中有趣的页面,那么从这个左下角页面开始。
它们跟随一个链接并移动到另外的一个页面,看了一些之后,发现不敢兴趣了,这样就停止了浏览。
然后,又一天,它在小吴的推荐下,在完全不同的页面进行浏览,跟随一个链接并移动到另外的一个页面,一旦失去兴趣就停止浏览。

像这样,重复从某个页面开始浏览,移动几页后便停止的操作,如果从互联网空间一侧进行观察,就像网页浏览的人:重复移动页面几次后传送到一个完全不同的页面。
量化随机游走模型
假设 1 - α 代表选择当前页面中的一个链接的概率。
α代表该人将传送到其他页面的概率。
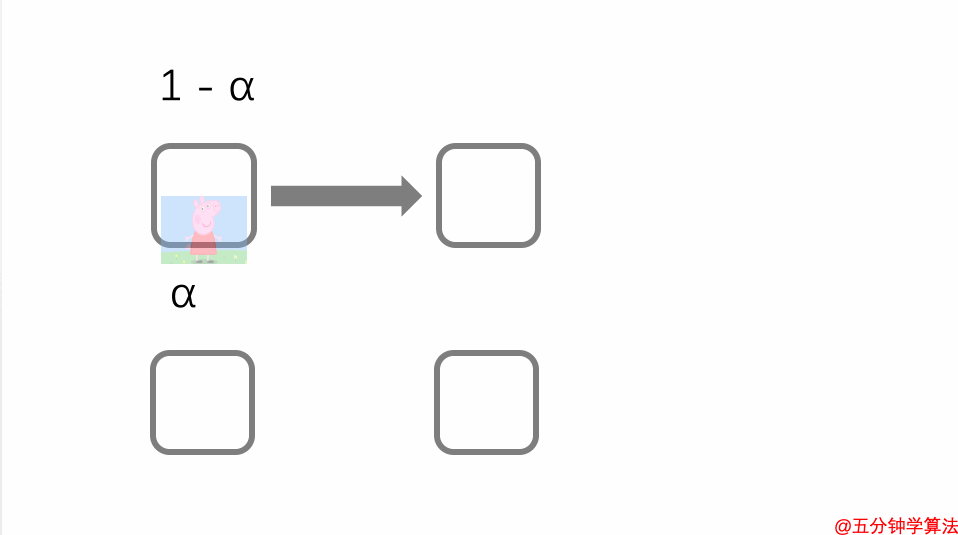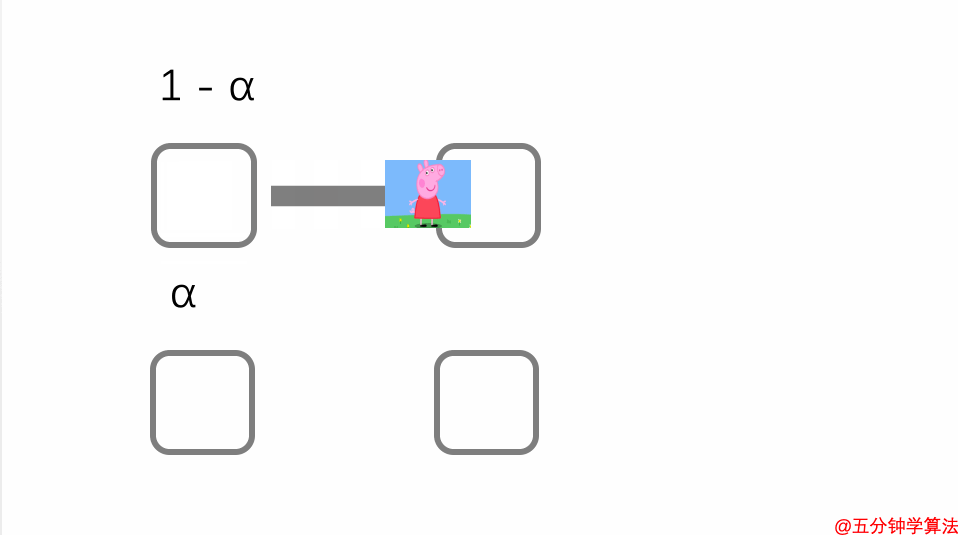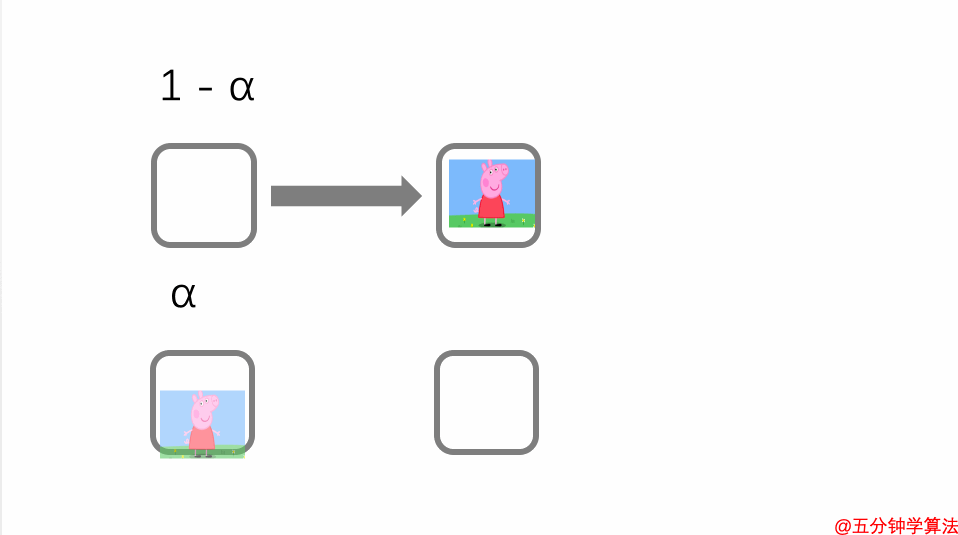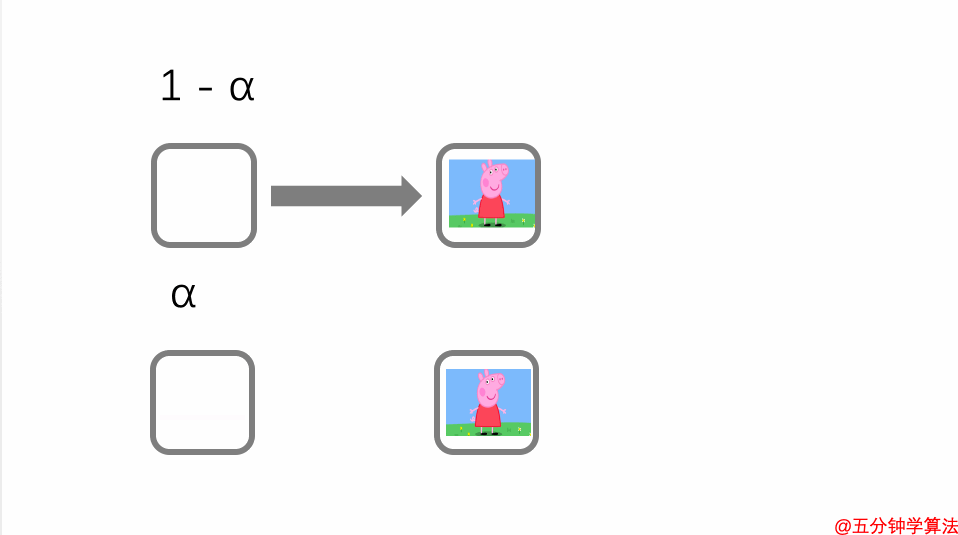
现在用随机游走模型 处理上述的循环问题。

如果总页面访问次数达到1000次之后,使用百分比进行表示:那么这个值就表示“在某个时间点查看页面的概率”。

更实用的计算方法
如图所示,现在来尝试计算复杂的链接网络中每个页面的分数。
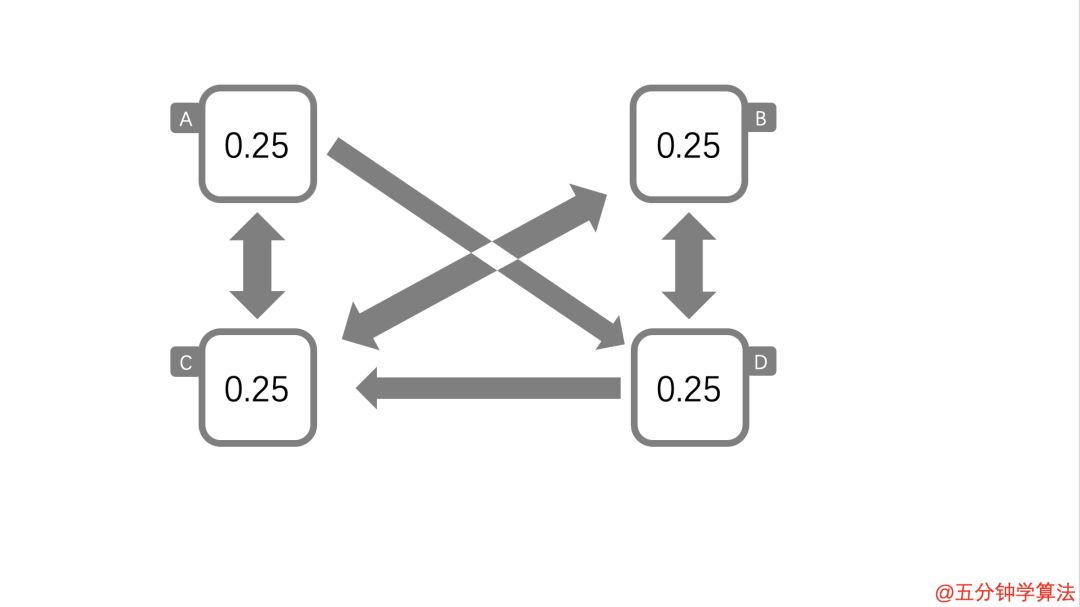
现在均匀设置分数,使总分加起来为 1 。而后根据网页浏览者的移动,来计算每个页面的概率。
移动 n次时出现在 A 中的概率表示未 PAn,移动 n 次时出现在 B 中的概率表示未 PBn。
举一个例子,在移动 1 次之后求在 A 的概率 PA 1。
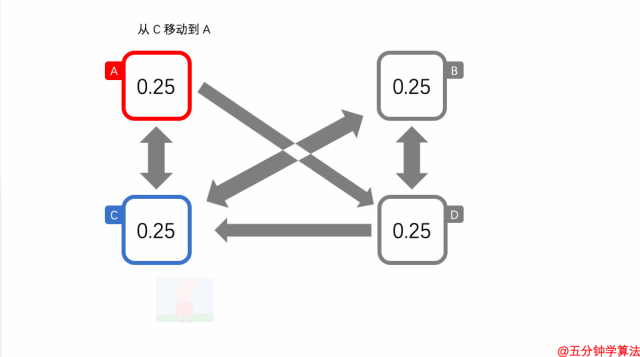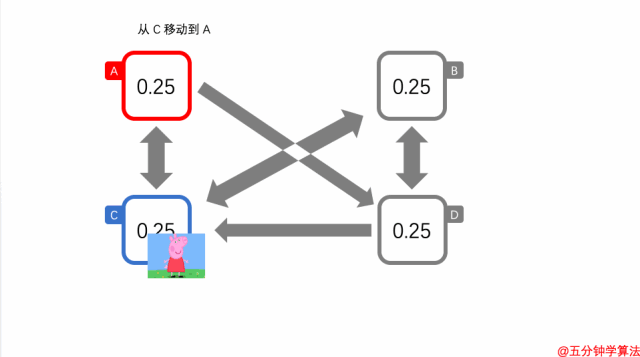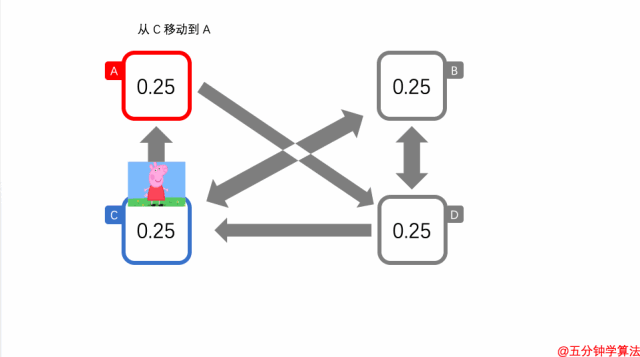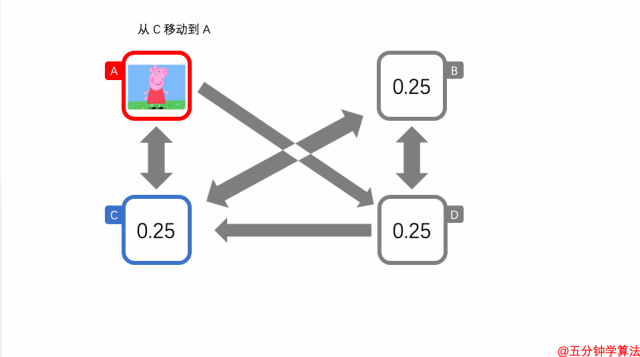
在 C 选择移动的概率是 1-α。
其中,移动到 A 的一种场景是,C 中的佩奇选择了移动而不是传送。另外,这里选择了 A 而不是 B 作为目的地。
并且,根据上面的当有多个网页的链接时,链接分数均匀分布这条规则,从 A 或 B 选择 A 的概率是 0.5 。

因此,从 C 移动到 A 的概率是 PC0 ✖️ (1-α) ✖️ 0.5。

A 被选为传送目标的概率是 0.25
A 被选为传送目标的概率是 0.25 ,根据前面的理论:在 A、B、C、D 中小佩奇选择传送的概率为 α。因此,通过传送移动到 A 的概率为 α ✖️ 0.25。 所以,移动一次后在 A 的概率为 PA1 = PC0 ✖️ ( 1 - α ) ✖️ 0.5 + α ✖️ 0.25
其中 PC0 = 0.25 , α = 0.15,代入计算后 PA1 = 0.14375。
这样,通过计算后 B 、 C 、D 页的概率也更新了。

B 、 C 、D 页的概率也更新了
上面在移动 1 次之后这四个页面的概率更新情况,根据上述相同的方法计算 2 次后小佩奇浏览在每个页面的概率。

移动 2 次后
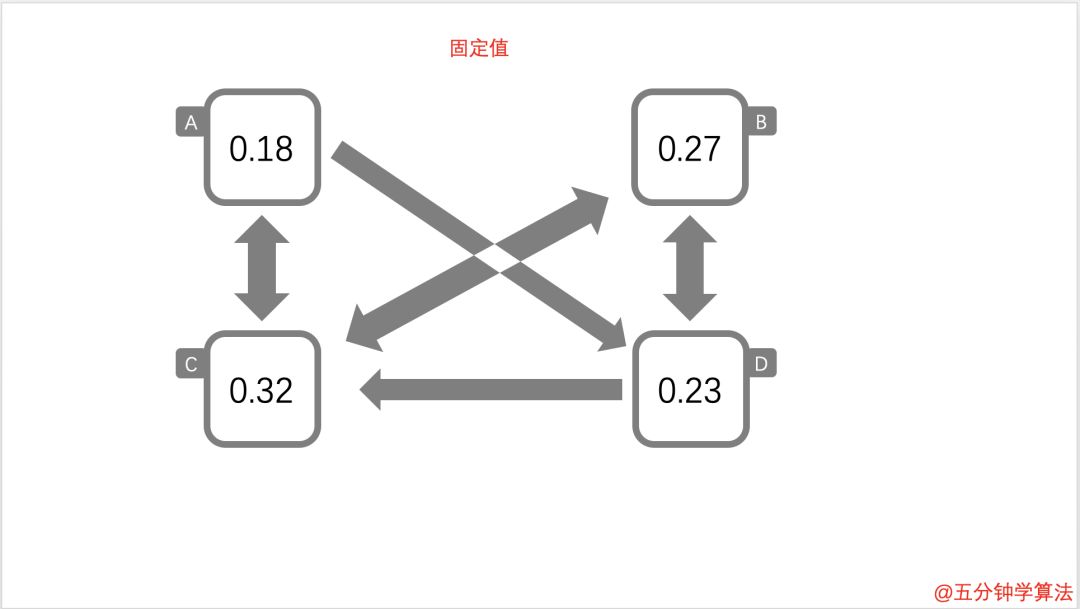
同样的,经过大量的移动,在每个页面上的概率逐渐趋于固定值。当数值固定是,计算也就完成了。
全部0条评论

快来发表一下你的评论吧 !

