

什么是Solidity正规验证
区块链
描述
Solidity作为一个程序语言,写出来的Smart Contract就跟所有程序一样,有时候会有Bug。然而Smart Contract上的Bug很可能比一般程序中的Bug还要严重,因为一旦放到链上就再也无法被修改了,最知名的莫过于DAO attack。于是有人将脑筋动到另一个依然还未被广泛应用的领域上— —正规验证(Formal Verificatinon,也有人称为形式化验证)。
本篇文章介绍的内容则是正规验证前必须的工作,即定义一个语言的语意(semantics)。在一个语言中,一个语句的语义指的是这段指令所代表的「意思」。看到这大家可能会有个疑惑,为什么一个指令的意思需要另外定义?不是全部都写在规格书跟编译器里了吗?原因是,就算是写在规格中的语法,其真正的意思也时常是没被精确定义的,如果仅是写在规格书中,那一个指令结束后,整个电脑的状态(在EVM可以指整个Ethereum的Global State)常是无法被确定的,必须了解编译行为、以及编译后的bytecode才能了解会发生什么事。然而一个好的程式语言,应该让程式设计师只看高阶的程式码就能判断会及不会发生什么行为。
什么是正规语意?以虚拟码与Hoare Logic 为例
一个典型用Hoare Logic进行分析的程式会具有三元的结构{ P } C { Q },不严谨的解释是对于一个程式C,其执行前的状态P(前件)会在执行后变成状态Q(后件)。状态P , Q都是由命题构成集合。
我们先看一句简单的指令:x := x+1
这个指令做的事很简单,「将x加上1后赋值给自己」。但在撰写程式时我们其实是对这个指令执行前与执行后会发生的事已经在脑内有许多的预设了,才会写下这样的程式。而Hoare Logic正是将这些脑内的预设写下来。例如,若我在写下这行程式时,我确信执行前的x的值为42,那在一个语法没有其他作用的程式语言中,这行程式执行完x的值会变为43。在Hoare Logic中可以写成{ x =42} x := x +1{ x =43}。
我们再看另一行程式
y := x
若在写这行程式时我们已经想好x的值会是43,那执行完y应当要是43。写成Hoare Logic便是{ x =43} y := x { y =43}。
当我们发现第一个程式的后件与第二个程式的前件相同,便能将上面两行程式连接起来,而变成{ x =42} x := x +1; y := x { y =43}。
从而在写一个程式时,我们若总是在每个小程式前后加上前件与后件(P与Q),最后在将所有程式组合起来时,就能确切知道这个程式在给定一个执行前的状态下,执行后必然会发生什么事。
在设计一个语言时,若我们所有最基本的单元操作的前后件都写出来,那就可以想像我们能设计一套工具去判断整个程式执行前后一定会发生的事,而不会有如C 语言中的undefined behavior 或需要看bytecode 才能确定的行为。
Matching Logic 与K-framework
K Framework是一个用来定义程式语言的工具,其运用的是Hoare Logic的延伸— — Matching Logic。在K Framework中,定义一个语言需要三个基本的元件:语法(syntax)、配置(configuration)与规则(rule)。
定义程式语法用的(K的)语法是BNF,若写过functional语言或读过计算理论的人可能会很熟悉,简单来说就是将一个语言中的所有可能出现的语法以递回的方式定义清楚,以这篇论文中定义Solidity的语法方式为例子:
K := uintm | address | K[ n ]
T := uintm | address | T[ n ] | T[] | mapping KT| ⟨ T ⋅⋅⋅ T ⟩ | contract | ref T
这部分只列出所有Solidity 可能出现的型别,若要完整定义语言还需列出如contract、pragma 等关键字。
而Solidity 写成K Framework 的语法实在太长了,这里就先以一个官网范例中简单的语言IMP 为例子(简写自imperative,相对于declarative 语言。其实定义纯functional 的declarative 语言相对简单,也是官方提供的第一个范例,但读者应该更熟悉如Solidity 或C 等imperative 语言因此也用此举例)
IMP 以K Framework 定义的Syntax 如下
module IMP-SYNTAX
syntax AExp ::= Int | Id
| AExp “/” AExp
》 AExp “+” AExp
| “(” AExp “)”
syntax BExp ::= Bool
| AExp “《=” AExp
| “!” BExp
》 BExp “&&” BExp
| “(” BExp “)”
syntax Block ::= “{” “}”
| “{” Stmt “}”
syntax Stmt ::= Block
| Id “=” AExp “;”
| “if” “(” BExp “)” Block “else” Block
| “while” “(” BExp “)” Block
》 Stmt Stmt
syntax Pgm ::= “int” Ids “;” Stmt
syntax Ids ::= List{Id,“,”}
endmodule
由此可以看出,对于任何一个指令Stmt,他都必需是Stmt所定义的形式中其中一种。如while(1){x=1+1;}是合法的Stmt,因为他符合“while” “(” BExp “)” Block的形式,而这是因为while中的1符合BExp的形式,而且x=1+1符合Stmt中Id “=” AExp “;”的形式,因为1+1符合AExp …依此类推。
而配置(configuration)则是将语言执行中会用到或改变的状态(state)写下来,这些配置可以是记忆体、计数器等。如果是完全没有副作用的语言那可能不需要定义这种状态(完全不需要输入输出的declarative 语言可能就用不到,如K Framework 在tutorial 中定义的小语言LAMBDA)。然而一般实务上使用的语言一定用到外部的状态,状态也能称为环境(enviroment),可以理解为从语言中看不出来,但在执行时会用到与造成影响的对象。如在C 中直接修改记忆体的操作,虽然语法上只是一个指令(指令执行的结果在后续程式中拿来使用),但实际上对「记忆体」这个状态造成了影响。以Solidity 来说实体的state 就是Storage 与Memory。真正需要定义的state 其实细分非常多,如Type Space(从变数名称到Type 的对应关系)、Name Space(变数名称到记忆体位置的对应关系)、Storage 与Memory(从记忆体位置对应到其上的值)等。
配置可以是巢状的,也就是说一个配置中可以包含其他配置。例如一个thread 中有一个stack,一支程式可以有好几个thread,就用得到这样的配置。
IMP 中的configuration 长这样:
configuration 《T》
《k》 $PGM:Pgm 《/k》
《state》 .Map 《/state》
《/T》
与庞大的语言比起来这是非常简单的configuration。语法是XML,一个configuration的空间称为一个cell,这里有两个cell,k与state。k里面放的是程式码本身,而state则储存了如变数等需要记录的状态。T可以暂时不理会。$PGM是K Framework的变数,意思是程式码要放在这个cell中(程式码也是环境的一部分!如在C中程式码也是data的一部分,甚至能写出能读写自己的程式码区块的程式),:Pgm说明这个程式码同时必须是符合Syntax中定义好的Pgm的形式才行。
configurations 也定义好后,就要写规则。规则就是最重要的「程式如何执行」的原则。在K Framework 定义的语言中,一行指令会做出什么操作,一定要是明确写出的一条规则才行,否则就会无法执行。一条规则的形式是「可被执行的程式」加上其「被执行成的结果」,另外能加上附加条件以及其会对环境(配置)造成的影响。如现在有条简单的规则:
rule while (B) S =》 if (B) {S while (B) S} else {}
这条规则是在说明,任何符合while (B) S形式的语法都能执行为if (B) {S while (B) S} else {}。=》这个动作可以称为重写(Rewrite),因为这规则的意思其实就是「将左边的程式重写成右边的程式」,再将重写后的程式继续依照其他规则执行(重写)下去。
再看另一条规则:
rule 《k》 X = I:Int; =》 。 .。.《/k》 《state》。.. X |-》 (_ =》 I) 。..《/state》
这条规则是在说,在k这个configuration中,当出现X=I形式时(I必须为Int),其会被重写为什么都没有(。在K Framework中是nothing的意思)。在《k》 《/k》中开头没有 。..,结尾却有,意思是若要使用这条规则,X=I的形式必须出现在程式的开头。而state中X所对应到的值会被取代为I。(|-》是变数名称与值的对应关系,_是本来所对应到的值,但因为不需要用到本来的值所以用_)
到这边为止应该可以看出,规则跟上面讲的Hoare Logic其实非常像!只是我们将前件后件写成了Rewrite的规则,{ P } S { Q }被转换成了S ∧ P ⇒ T ∧ Q这样的形式(T是Rewrite后的程式码)。
K-framework 中被正规化的 Solidity
写了这么多,这篇跟本还没讲和Solidity 有关的内容。的确,光是介绍K Framework 就花了很多功夫,在开头提及的论文中,南洋理工与新加坡科技设计大学的人将Solidity 的基本语意实作在K Framework 中,写了50 个configuration 以及200 多条rule(2000+ 行),目前已经可以在K Framework 中执行。在执行过程中,我们就能做动态的测试,判断cell 中会不会出现预期以外的值。
我们就看其中一条简单的rule。
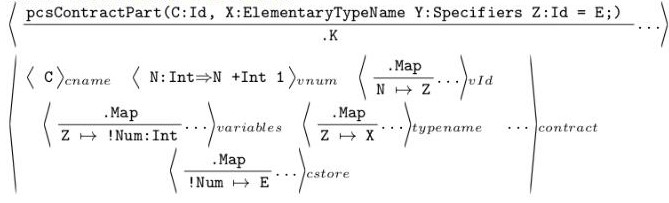
(注意这里的水平分隔上下就是⇒ 的左右)
Elementary-TypeName这条规则中,pcsContractPart是一个定义在K Framework的函数,会被展开为一个可以被重写的形式。(在《k》中的)程式码若是符合一个变数宣告的形式,contract cell中的许许多多配置就能够方式如上的操作。以uint public data = 10;为例,uint可以代入X(ElementaryTypeName)、public代入Y(Specifiers)、data代入Z(Id),10代入E。当出现符合这样规则的程式后,这行指令的下一步可以被「重写」为什么都不剩(.K,「。」开头为nothing的意思)。同时,在这个程式执行时的状态,也就是configuration中:
· cname(合约名称)必须有符号 C
· vname (记录变数数量)中的数字N 会增加 1
· vId (记录第N 个变数的变数名称)会多出一条N 到Z 的对应
· variables (从变数名称到变数地址的对应)会多一个Z 到 !Num 的对应,!Num 是告诉K 产生一个新的数字作为地址
· typename (记录从变数名称到Type 的对应)多一条Z 到X 的对应
· cstore (记录从地址到值的对应)多一条 !Num 到E 的对应。
需要注意的是,每个cell 中的前件都要成立,这个规则才适用。如果前件为nothing(「。」开头),那就代表这个cell 没有前件。例如,若contract cell 中没有C 这个合约名称,这条规则就不能被使用。如果一行指令没有任何规则能被套用,程式就会执行不下去。
结语
语意正规化后,离正规验证其实还有段距离。若我们想要验证一个程式的正确性,我们得先将我们所认为的「正确」的条件(specification)给列出来。例如,在一个扣款的合约中,钱包被扣除的数字必须只能有一次,我们就能另外写程式检查在存有钱包金额的那个cell中,是不是一定只会减少某个数字。但这样的程式要怎么写又是另一个大工程,其中牵扯到将Matching Logic转换成可以被验证的逻辑模型等问题。已经有人将EVM实作在K Framework中(注意不是Solidity,在计算理论中,要描述一个完整的程式语言与描述一台电脑是等价的,EVM同理也能以K Framework描述),并配合Z3证明器写了用来证明Smart Contract的工具,里面附有一些已经证明好的Smart Contract与他们的specification,有兴趣的人可以了解一下。
-
[原创]国家正规刊物征稿2009-06-04 0
-
[原创]国家正规期刊联合征稿2009-08-26 0
-
国内那几家是正规Nordic代理商?2015-12-22 0
-
ETH之Solidity:Solidity的简介、安装、使用方法之详细攻略2018-12-21 0
-
3种正规电线接头的方法2018-01-17 21337
-
简单介绍Solidity的语法2018-05-03 5468
-
hanlp源码解读之字符正规化CharTable2018-10-18 254
-
以太坊的Solidity是什么2019-01-17 3028
-
以太坊的编程语言Solidity在TRON中异步调用的应用2019-06-27 1090
-
如何使用Solidity编写智能合约的异步交易模式2019-07-05 840
-
家用配电箱正规接线图及安装说明2019-08-07 221896
-
如何写一个Solidity智能合约2019-09-05 2508
-
基于solidity的智能合约在tron网络异步调用怎样来实现2019-10-15 1257
-
什么型号的扬尘监测设备才是正规的?2021-12-15 506
-
怎么选择正规LED透明屏厂家?2023-06-30 1118
全部0条评论

快来发表一下你的评论吧 !

