

基于距离徙动校正的弹速补偿FPGA实现方法
可编程逻辑
描述
针对高速运动平台弹速补偿的实时性要求,在基于距离徙动校正(Range Cell Migration Compensation,RCMC) 的思想上提出了一种弹速补偿的FPGA实现方法。将距离徙动校正的思想用于弹速补偿,提高了相参积累后的信噪比,并在FPGA中完成硬件实现,仿真实验表明使用FPGA实现弹速补偿方法具有实时性高、处理速度快、精度高等有优点。
高速飞行器具有重要的战略意义和极高的应用价值,其具有全球攻击、机动作战等特点,特别是在远程打击、快速突防、电子压制、对地侦察和预警等方面极具发展潜力[1]。目标检测性能优劣是实现高速运动飞行器对目标精确打击的关键。对于高速运动飞行器而言,雷达导引头接收到的各脉冲回波间,由于平台速度引入了不可忽略的距离走动,严重降低相干积累后的检测前信噪比,从而直接影响整个雷达导引头的探测性能,因此必须对弹速产生的距离徙动进行补偿。
近年来,现场可编程逻辑门阵列(Field Programmable Gate Array,FPGA)技术飞速发展,集成度越来越高,功耗、成本不断降低,特别是在并行处理、流水线设计、可重构等方面具有独一无二的优势,使其逐渐在雷达信号处理领域中占据重要地位。本文使用FPGA对距离徙动校正算法进行了硬件实现,具有实时性高,处理速度快,精度高等特点[2-3]。
1 RCMC算法
弹载雷达弹速补偿方法采用了RCMC的思想,本节将从信号模型的角度对RCMC原理简要地阐述[4]。
假设一弹载雷达发射一串载频为f0,带宽为B,脉冲持续时间为Tp的线性调频信号,发射的脉冲串信号可表示为:


距离徙动校正(RCMC)是通过补偿各次脉冲的时间延迟Δti,使得第i(i=2,3,…,N)个脉压输出时域信号峰值位置按第一个脉冲对齐。第i次脉冲的RCMC补偿因子的频域形式可表示为:

综上,只需对距离压缩后的回波信号在频域乘以一个距离徙动校正因子Hi(f),就可以去掉距离走动效应。所以弹速补偿的实现方法的核心问题就是让硬件来运算式(11)。
2 算法的FPGA实现
由于FPGA在并行处理、流水线设计、可重构等方面的优势,使其相对于DSP等处理器更适合来运算式(11)。具体的实现方法按流程上可分为三步来做,第一步是将时域信号变为频域信号;第二步在频域下乘以Hi(f);第三步将运算结果逆变为时域信号。显然,第一步和第三步使用FFT和IFFT即可实现,并且FFT和IFFT算法的FPGA实现已很成熟,所以实现方法的核心问题就是实现第二步。
在做RCMC之前首先要在FPGA内做数字下变频和脉冲压缩,由于距离徙动校正和脉压有紧密的互联结构,在硬件设计中,特别是同步设计上,往往要将这两者综合考虑,所以本设计中将脉压和距离徙动校正封装在一个模块内。
接下来按照功能来介绍,先对脉冲压缩进行简要介绍,再对距离徙动校正作详细介绍。图1为距离徙动校正模块的系统框图。RCMC模块的顶层的输入输出很简洁,输入输出端口与式(11)、式(16)中的参数的映射关系如表1所示。
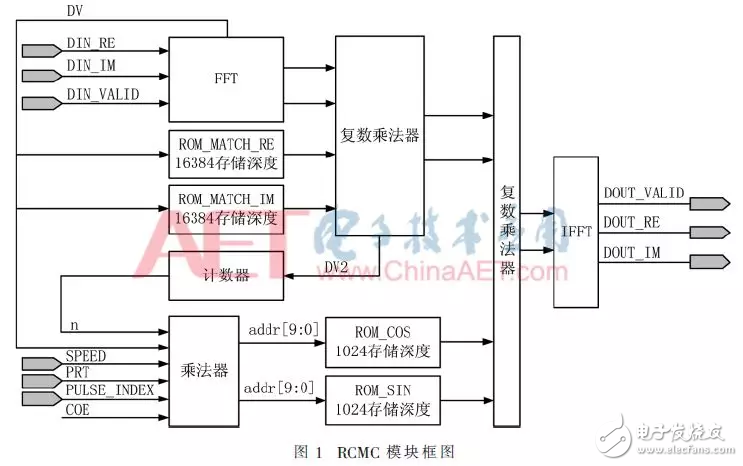
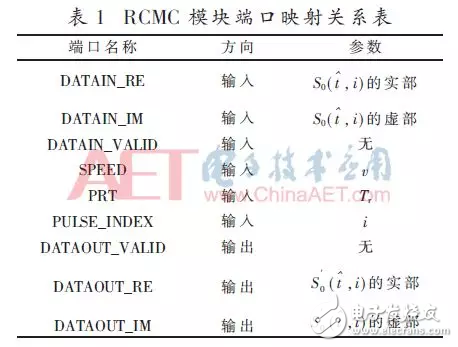
2.1 脉冲压缩的FPGA实现
脉冲压缩在时域下是回波信号与匹配滤波器的冲击响应的卷积,而在频域下为乘积运算,便于硬件实现。所以本设计中采用频域下相乘的方法来实现时序脉冲压缩。
将输入的两路正交回波信号DIN_RE和DIN_IM进行FFT运算,XILINX提供了免费的FFT IP核,所以这里直接在FPGA工程中调用一个FFT IP。将DVIN与FFT的start引脚连接,将输入数据DIN_RE、DIN_IM与FFT的xn_re,xn_im连接。然后将经过FFT运算后的两路频域数据与量化后的匹配滤波系数复乘。匹配滤波系数由MATLAB生成导入FPGA的ROM内。如图1所示,ROM的使能引脚与FFT的输出有效引脚dv连接,ROM使能之后地址累加1开始输出系数,与FFT输出的数据作同步处理之后输入给复数乘法器,若不作距离徙动校正将复数乘法器的结果进行逆FFT运算之后便完成了脉冲压缩。
2.2 距离徙动校正的FPGA实现
由式(10),可令:
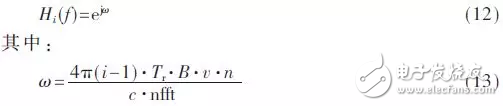
其中,i为脉冲序列数,初始值为1;Tr为慢时间域下的脉冲重复周期(单位:s);v为导弹速度(单位:m/s);c为光速(单位:m/s);f为单一频点的频率(单位:Hz);B为脉冲宽度(单位:Hz),这里取40 MHz;nfft为FFT的字长,这里取16 384;n为量化后的序列数,初始值为0。
对于FPGA来说,它无法直接计算ejω,而根据欧拉公式可得:

所以为便于FPGA实现可以通过正余弦函数来计算ejω。正余弦函数本文采用查表法的方式来实现,首先由MATLAB生成两组数据,数据值为round(G·cos(k))和round(G·sin(k)),G=8 192,k的取值范围为1:1:1024。G与k的取值与精度要求有关。将生成的这两组数据分别存在两个coe文件中。在FPGA工程中调用两个ROM,将存储深度定为1 024,位宽定为15,将MATLAB生成的两个coe文件导入ROM。如图1所示,再将ROM的使能与FFT IP核的dv引脚连接,通过计算ROM的地址即可计算得出的ejω的数值。具体计算方法如下。

式中,addr为ROM的地址,ROM的存储深度为1 024,所以sin与cos函数每1 024个数据为一个周期,所以要计算得出cosω与sinω,只要通过乘法器计算出addr,再将addr对1 024取余,即截取addr的低10位,然后接入两个ROM的地址总线引脚,接着把两个ROM输出的数据除以8 192,即截掉低15位,得到cosω与sinω的计算结果。
对式(15)的参数进行整理,将B、c、nfft等常数合并为系数coe,并取整得:

如图1所示,将两个正余弦ROM的输出与脉压之后频域下的数据作复乘(数据同步之后输入复数乘法器)即可完成ejω的运算,最后再对复乘结果进行逆FFT运算(IFFT IP核的设置与上文的FFT IP核的设置相同),即可得到脉压和距离徙动校正之后的数据。
3 仿真结果
本节将通过测试和仿真等手段来验证本方法的正确性和硬件系统的性能。
3.1 测试数据
为验证本方法的正确性和可行性,将一组(10个脉冲)下变频之后的回波数据输入FPGA进行运算,在复数乘法器1的输出口和整个系统的输出口设了两个测试点,将这两个测试点的数据保存至txt文件,导入MATLAB,与直接用MATLAB作距离徙动校正后的数据进行对比。
输入的初始回波数据如图2所示。
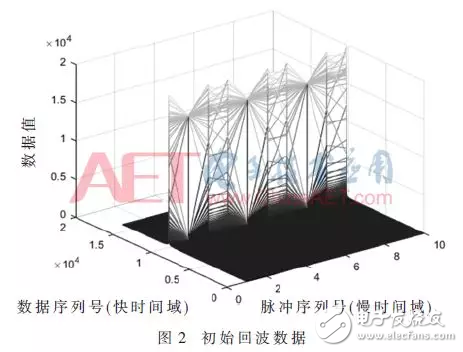
第一个测试点数据作折线图,如图3所示。MATLAB的仿真结果如图4所示。
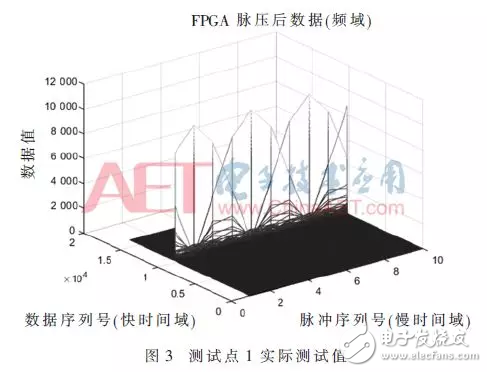
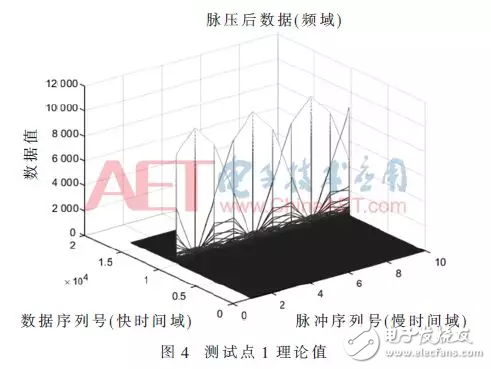
第二个测试点数据作折线图,如图5所示。MATLAB的仿真结果如图6所示。
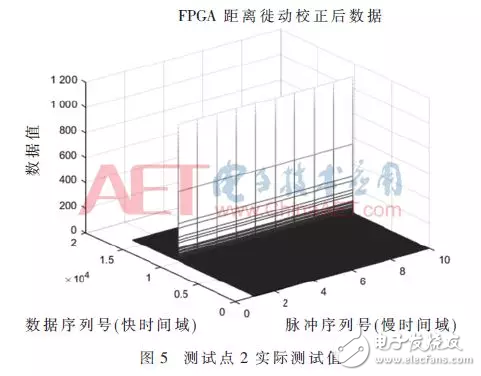
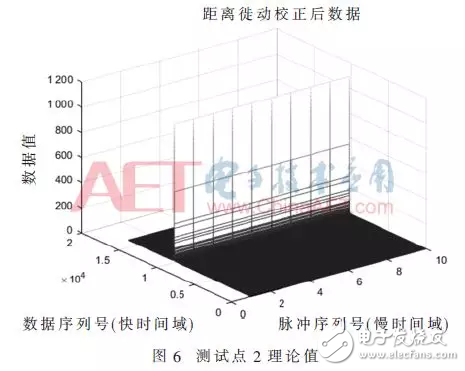
由上面两图可以看出FPGA运行结果与MATLAB仿真结果非常一致,将测试点2的两个数据做差可以看出误差,如图7所示,可以估算出最大误差为1.5/1 100=0.14%。
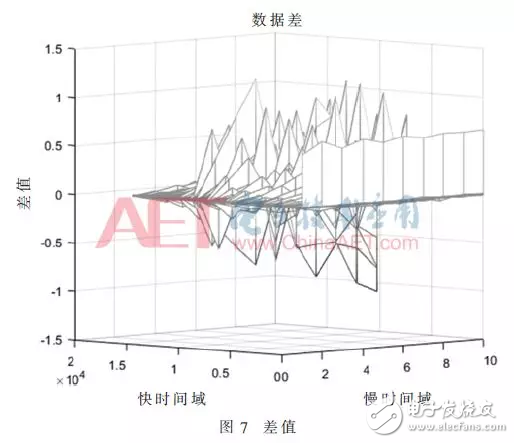
3.2 仿真波形
图8是MODELSIM仿真波形,以一个脉冲数据为例,可以看出,从第一个回波数据输入到系统处理结束后最后一个数据输出,整个系统的处理时间为493.355 μs,扣除数据传输时间16 384×5 ns=81.92 μs,系统处理时间为411.435 μs。

在FFT处理出第一个数据的瞬间,使能信号就会传递给ROM_MATCH和乘法器模块,这些模块便开始进行运算,并且FFT每输出一个数据,这些模块便计算一次,当16 384个数据全部FFT运算结束,其他模块也几乎同时运算结束,数据从FFT输出到复数乘法器输出结果延时时间小于20个时钟周期,本系统的主时钟频率为200 MHz,所以延时时间小于100 ns,很好地体现了FPGA并行处理和流水线运算的优势,总延时493 ?滋s绝大部分都消耗在了FFT和IFFT运算以及数据传输时间上。
4 结论
将距离徙动校正的思想用于弹速补偿,提高了相参积累后的信噪比,使用FPGA实现距离徙动校正算法具有实时性高、处理速度快、精度高等特点,为雷达导引头提供了很好的软硬件支持,提高了雷达导引头的探测性能。
-
一种基于FPGA的DSU硬件实现方法2019-06-28 0
-
传感器线性校正方法的原理是什么?2019-10-30 0
-
基于FPGA的两点非均匀校正模块的设计与实现2009-08-15 598
-
基于GPS信号的双基SAR数值距离徙动成像算法2009-11-09 743
-
距离徙动校正和斜地变换的实时算法研究2009-11-18 3349
-
基于FPGA的正码速调整的设计与实现2010-01-13 595
-
低脉冲重复频率下成像方法研究2011-05-19 689
-
PI校正补偿威廉希尔官方网站2012-04-28 9314
-
基于FPGA的数字稳定校正单元的实现2012-06-26 799
-
三目立体视觉外极线校正及其FPGA实现方法2016-09-17 672
-
一种弹速补偿的FPGA实现方案解析2020-12-14 1975
-
在距离多普勒处理中使用Keystone变换进行距离徙动校正2023-12-04 2167
全部0条评论

快来发表一下你的评论吧 !

