

离散信号的频域分析——离散傅里叶变换DFT
描述
文字简明扼要,语音更加详细生动哦。
继续上一篇,本文对离散信号的频域分析(共5节)中的第3节——离散傅里叶变换DFT(Discrete- Fourier Transform)中的第4个问题:3.4 DFT性质中的后两个进行讲解。

3.4 DFT的性质
以下四个性质,上一篇中已经学习了前两个,本文对前后个性质——圆周共轭对称性、Parseval定理进行讲解。

3、圆周共轭对称性
这里不讲证明(教材上都有),重点讲怎么理解教材上让人眼花缭乱的公式。我们把“公式”翻译成“人话”。
首先说明一下,本文中所说的N点长序列,都指的是自变量取值范围为0~N-1,除此之外的区间,序列值为0。
先看第一个。
(1)共轭序列的DFT
时频域有这样一个基本对应关系——时域取共轭,对应频域自变量取负然后函数取共轭。具体到DFT呢?“自变量取负”也就是“反转”,而“DFT隐含着周期性”,所以这里的“反转”要加上“周期延拓,再取主值区间”,所以,公式及证明过程如下:

图1
时域取共轭,对应DFT是:先周期延拓,再反转,再取主值区间,最后取共轭。当然,第一步与第二步可以交换次序,取共轭可以放在任意步骤上。关键是理解这个操作用公式的三种描述方式(上图中画红线处)
第一种:X*((-k))NRN(k),是最直观地展现上述过程的;
第二种:X*((N-k))NRN(k),可以认为是利用其周期性(周期延拓得到的当然是以N为周期的啦),把-k换成了N-k;
第三种:去掉了双括号,也去掉了RN(k),好像看不出“周期延拓”和“取主值区间”的操作了。大家会心存疑虑,这个等号成立吗?
我们用下图的例子来说明一下这个等号成立,为了画图的方便,我们用函数值为实数的情况,图中是以n为自变量,换作k当然也是一样的。

图2
x(N-n)可以看作简写形式,优点在于形式简洁明了,缺点在于掩盖了周期延拓再取主值的过程。用这种简写形式,要注意一点,N点长序列x(n),n的取值范围为0≤n≤N-1,也就是说,本来应该x(N)=0。但是,此处,当n=0时,x(N-n)=x(N),不能认为x(N)=0,而要认为x(N)=x(0)。也就是说,要把x(n)的这N个点,认为是周期序列的主值区间,那么x(N)就是下一个周期的第一个点,所以x(N)=x(0)。
用这种简写形式来描述这个性质,就是:时域取共轭,对应的DFT,相当于把序号k与序号N-k做一个互换,然后取共轭。
下面,看这个性质的两个推论。
(2)第一个推论:实序列的DFT是圆周共轭对称序列。

图4
(此处省略若干公式)
”圆周共轭对称“是个什么鬼?
我们按照以下几步来解释一下:
第一步:从“偶对称、奇对称”到“共轭对称/共轭反对称”
偶对称/奇对称地球人都知道吧。共轭对称/反对称就不是地球人都知道了,大学生才知道。
对于实函数x(n),如果x(-n)=x(n),称之为偶对称,x(-n)=-x(n)称之为奇对称。
扩展到复函数x(n),如果x*(-n)=x(n),称之为共轭对称,x*(-n)=-x(n)称之为共轭反对称。
第二步:从“共轭对称”到“圆周共轭对称”
圆周共轭对称的定义:对于N点长序列x(n),如果x(n)=x((N-n))NRN(n),或者用简写形式:x(n)=x(N-n),那么称之为“圆周共轭对称”。
可以理解为:把x(n)放在一个圆周的N个等分点上,或者说把横轴掰弯,弯成一个圆(n=N-1与原点重合),则这N个序列值关于原点对称,或者说关于N/2也对称。如下图所示。
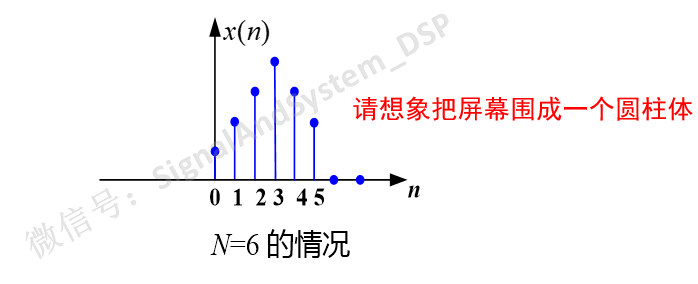
图5
我们前面求解过的例题:5点矩形脉冲的DFT,如下图,也体现出圆周偶对称的特点。
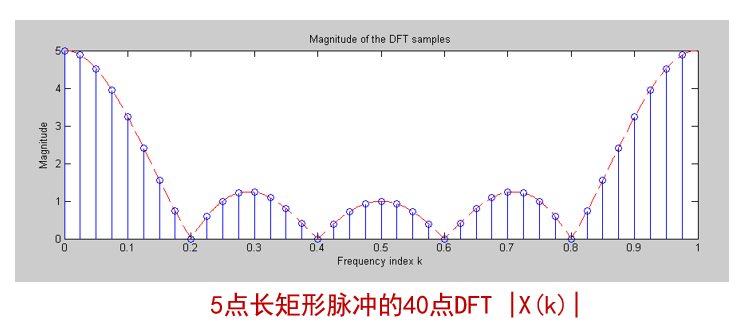
图6
(3)第二个推论:实部/虚部与圆周共轭对称/反对称分量的关系
首先解释一下什么叫圆周共轭对称分量和圆周共轭反对称分量。需要经过以下几步循序渐进的理解。
第一步:函数可以分解为偶分量+奇分量

图7
第二步:从“偶分量/奇分量”到“共轭对称分量/共轭反对称分量”
把(1)式中的x(-n)改为x*(-n)即可

图8
以上两式,无论是对无限长序列,还是有限长序列,都是适用的。如果x(n)为N点长,并且0≤n≤N-1,那么xe(n)和xo(n)是2N-1点长,并且-(N-1)≤n≤N-1。
第三步:改造成适合DFT的
凡是涉及到自变量取负(也就是反转)的,都加上“周期延拓,再取主值区间”的操作。也就是把(2)式中的x(-n)改为x((N-n))NRN(n),用简写形式表示就是x(N-n)
因此,得到圆周共轭对称分量和圆周共轭反对称分量的定义:

图9
注意,前提是x(n)为N点长序列,并且n的范围是0≤n≤N-1,圆周共轭对称/反对称分量的长度仍是N,n的范围也不变。而且如前所述,n=0时,x(N-0)=x(N)=x(0)。
上面,是以x(n)为例,同样,对于DFT X(k),也可以定义圆周共轭对称/反对称分量,不再赘述。
解释完这些,我们的核心公式就出来啦(证明过程省略,直接看结论)。
序列 x(n)及其DFT的实部/虚部与圆周共轭对称/反对称分量之间的关系 ,见下图:

图10
(此处省略若干公式)
翻译成人话(绕口令)就是:
序列实部的DFT是序列DFT的共轭对称分量
序列虚部×j的DFT是序列DFT的共轭反对称分量
序列共轭对称分量的DFT是序列DFT的实部
序列共轭反对称分量的DFT是序列DFT的虚部×j
是不是像绕口令,但总比公式强多了。
这一切,意义何在?
第一,从图形上可以淋漓尽致地体现DFT隐含的周期性。
第二,为DFT的简化运算提供了思路。
4、Parseval定理
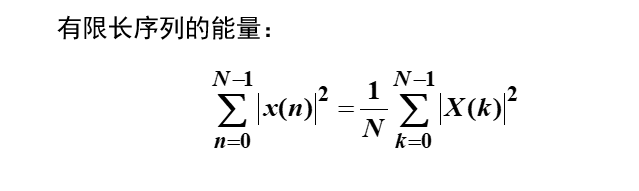
图11
-
图像频率域分析之傅里叶变换2019-05-22 0
-
离散傅里叶变换DFT在电阻网络分析中到底起到什么作用2022-08-19 0
-
离散时间信号分析和处理2008-10-02 2246
-
离散傅里叶变换及其快速算法2008-10-30 849
-
离散傅里叶变换,(DFT)Direct Fouriet Tr2009-07-25 2052
-
有限长离散变换-离散傅里叶变换2011-02-23 1096
-
离散傅里叶变换(DFT)2016-12-28 904
-
离散傅里叶变换(DFT)及其快速算法(FFT)2016-12-28 935
-
数字信号处理第3章-离散傅里叶变换(DFT)2016-12-28 954
-
数字信号处理(第三章-离散傅里叶变换DFT)2016-12-28 993
-
数字信号处理[第三章-离散傅里叶变换(DFT)]2016-12-28 989
-
数字信号处理--第3章--离散傅里叶变换(DFT)2016-12-28 992
-
使用DFT分析离散信号频谱的实验资料免费下载2019-08-06 1439
-
傅里叶变换和离散傅里叶变换的关系2023-09-07 2611
-
DFT与离散时间傅里叶变换的关系 DFT在无线通信中的应用2024-12-20 684
全部0条评论

快来发表一下你的评论吧 !

