组合29个简单Python代码块，自动发现新算法

英特尔的研究人员提出一种新的自动算法生成器（AAD），利用演化算法框架，以Python语言的基本子集作为语法架构，能够对29个数组/向量问题的代码块进行组合，通过学习，自动生成更复杂问题的解决方案。

本文介绍一种自动算法发现器（AAD），这是一种用于合成高复杂度计算程序的演化算法框架。此前的演化算法依赖于客观的适应函数，这在给算法设计上增加了难度。

本文提出的AAD采用问题式引导演化过程（PGE），这需要将一组问题一起引入，针对更简单问题发现解决方案，用于解决同一组问题中的更复杂的问题。 PGE还支持几种新的进化策略，并自然地应用于高性能计算（HPC）技术。

AAD可以为29个数组/向量问题生成Python代码，范围从min，max，reverse到更具挑战性的问题，如排序和矩阵向量乘法。此外，AAD显示出对受限环境/受限输入的强适应性，以及针对“开箱即用”的问题的解决能力。

AAD是将相对简单的问题解决组件自动组合程序，可以实现搜索由这些组件的所有可能排列所组成的整个空间，然后寻找满足给定要求的解决方案。目前已经提出了许多这样的搜索策略（例如枚举，基于演绎，约束求解，随机）来应对这类挑战。

使用AAD的分类算法代码块示例

本文提出了一种基于演化算法的搜索策略，将其AAD中实现。AAD可以基于Python的子集作为语法结构，组合成复杂度相对较高的程序（循环，嵌套块，嵌套函数调用等），并生成可执行的Python代码。在本文中使用AAD来发现数组/向量问题的算法解决方案。

总的来说，AAD实现了以下目标：

使用问题导向型的演化策略来消除算法中的目标函数。

使用多样化的演化策略（多环境解决方案，异花授粉和联合演化），并通过广泛的实验评估其有效性。

利用AAD解决通用Python语言中的29个数组/向量问题，表明演化算法能够解决复杂的新问题。

支持循环模块，可以发现任何（非零）输入的算法。

AAD结构设计方案和原理

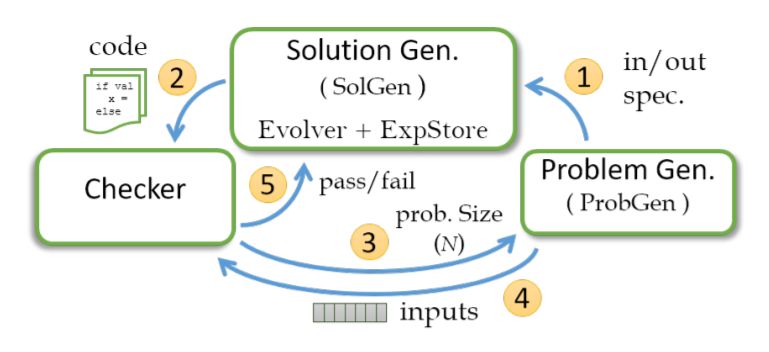
AAD主要架构示意图，主要由问题生成器、解决方案生成器和检测器组成

问题生成器（ProbGen）

我们想要解决的每个问题都从问题生成器开始。 这部分负责：（1）指定输入和输出的数量和类型。（2）为给定的问题生成输入。例如，对于最大查找（Max），问题生成器指定Max将一个数组作为输入，并生成一个数字作为输出。另外，当请求为大小为N的问题生成输入时，会产生一个由N个数字组成的输入数组。

检测器（Checker）

检测器负责接受/拒绝为给定问题生成解决方案。 检测器使用问题生成器生成的输入执行生成的程序，并生成输出。检测器中包含接受/拒绝输出的逻辑。因此，检测器与给定的问题生成器对应，两者齐头并进。

检测器不一定真正需要实现其想要发现的算法。比如，针对“排序问题”的检测器不必对真的对输入数组进行排序，而是可以比较输出数组中的每两个相邻元素，并查看这两个元素是否按预期顺序排列。一旦检测到未排序数据对，检测器会做出“失败”的声明。如果每对相邻元素都是有序的，并且输出数组中包含的元素与输入数组完全相同，则检测器宣布可接受该解决方案。

解决方案生成器（SolGen）

SolGen主要由两部分组成：（1）表达式/短语存储，以及（2）演化器。

表达式/短语存储器（ExpStore）

解决方案生成器使用语法构造源程序。 AAD使用的Python语法子集存储在ExpStore中，如表1所示。在AAD中，语法规则使用类型信息进行扩充。

AAD支持四种数据类型：数字（NUM），布尔数（BOOL），数组（ARR）和数组的数组（AoA），它们可以对矩阵进行建模。此外，表达式的每个操作数都标记为Consumer（只读），Producer（只写）或ProdCon（读-修改-写）。

演化器（Evolver）

演化器负责对表达式和短语进行组合，以生成程序（或函数），以解决问题生成器提出的问题。演化器分三个阶段构建解决函数（SolFunc）。

阶段1：构建解决函数

阶段2：在“生产者”（只写数据）和“消费者”（只读数据）间建立联系

阶段3：操作和函数调用突变

检查输出

一旦解决函数构建出来，就会执行这个函数，使用Python的exec（）函数生成输出结果。检测器负责检查输出，判定接受或拒绝输出。如果第一个输出被接受，则使用问题生成器生成的更多不同大小的、与输入测试相同的解决函数。如果检测器接受了所有测试，则该解决函数即被声明为该问题的解决方案。上述三个阶段构成了一个循序渐进的步骤。

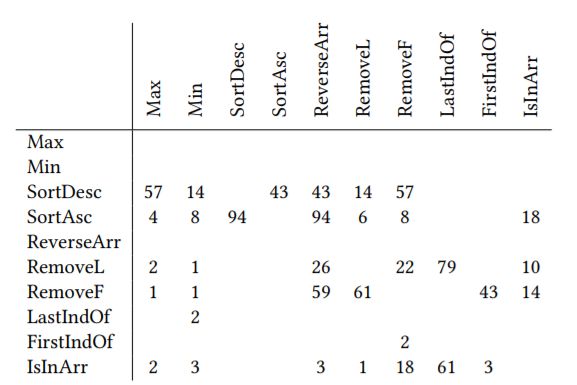
上表所示为在问题集A中的调用者-被调用者的关系。比如SortDesc函数所在的行显示，SortAsc在57％的解决方案中调用了Max函数，在14％的解决方案中调用了Min函数，以此类推。Min，Max和ReverseArr函数没有调用任何其他函数。所有其他函数都依赖于一个或多个函数来得到解决方案，显示出函数组合的重要性。

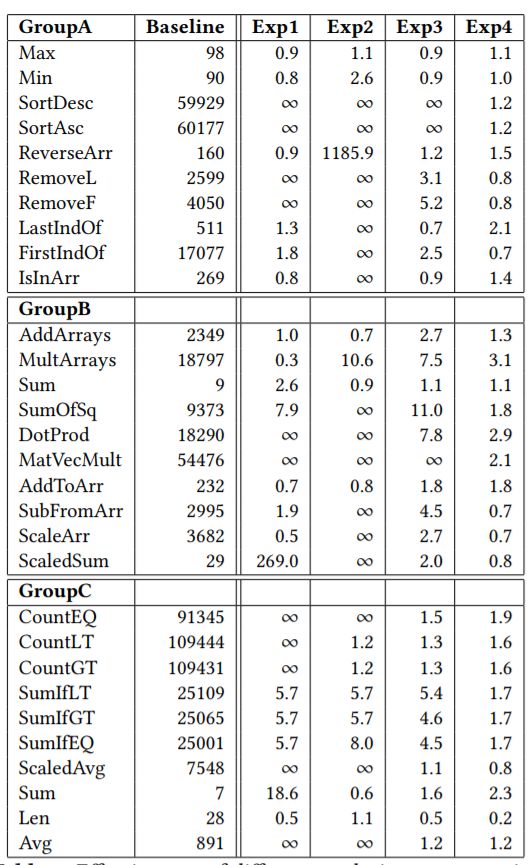
上表中列出了3组问题以及在基线方法下的步数表现，并将其与四种演化策略下的表现进行了对比。

未来前景与应用方向

从概念上讲，AAD也可用于程序翻译。对于用C语言，汇编语言甚至二进制语言编写的程序，可以执行该实例作为AAD的检测器来生成Python（或类似语言）代码。这种方式与仅通过观察另一个对象行为，来构建自身行为方式的机器学习算法类似。很明显，本文中使用的Python代码可以被视为“Python到Python”的翻译，因为不同的检测器对应了不同的Python实现。

AAD可能不仅仅是一个程序合成器。它还可以用来获取机器的内在知识。通过调用-被调用关系图和父子图捕捉不同问题之间的内在关系。这些关系是由AAD本身发现的，并且可以被认为是不同操作之间的联想记忆的一种表示，其形式与人类大脑构造和机制类似。

由于AAD可以通过引入越来越多的问题来增加知识储备的扩展，通过适当的指导机制，就可以引导系统获取大量技能（算法），并自己构建知识表示。就像我们在自己孩子还小时，向TA们提出许多问题和挑战，目的是为了引导孩子们获得大量技能和知识。

AAD是用于综合高复杂度程序的演化框架，它以Python语言的基本子集作为语法架构。使用AAD能够对29个数组/向量问题的代码块进行组合，其中既有最大值、最小值，矩阵翻转这类简单问题，也有更具挑战性的问题，如排序和矩阵向量乘法等，对于输入没有大小限制。

我们评估了解决这些问题策略的有效性，并证明了AAD具备解决“开箱即用”问题的能力。为了应对复杂需求带来的各种挑战，AAD工具还能实现与高性能计算（HPC）技术的结合。总的来说，与现有技术相比，采用PGE的演化算法能够解决类似或更高复杂性的问题。