激励相容的经济激励机制在区块链中的运用

区块链为非中心的、自组织的社区化经济形态提供了实验基础，良好的社区化运作除了需要共识机制来保障其安全和性能之外，还需要巧妙设计的经济激励机制来协调多个参与方的行为。

漠水云，Annchain核心成员，上海交通大学物理学博士，负责区块链社区的机制设计、区块链政策与市场趋势方向的研究。

晔不，Annchain核心成员，康涅狄格大学金融风险管理硕士。负责区块链项目和应用研究分析、经济激励机制设计。

什么是激励相容？

“激励相容”（incentive compatible）这一概念来自诺贝尔经济学奖得主里奥尼德·赫维茨（Leonid Hurwicz）创立的机制设计理论。机制设计的目标是使一个基于给定参与人的社会选择函数实现最优化。机制设计试图通过实施一个博弈规则来达到该目标。

激励相容：在市场经济中每个理性经济人都会有自利的一面，其个人按自利的规则行动。激励相容是指对于一定的经济环境和社会目标，如果能有一种机制使人们在自利行为驱使下采取的行动，正好使预定目标得以实现，那么这一机制就是激励相容的。

以太坊创始人Vitalik Buterin等人提出了有关优化配置公共物品的“自由激进主义”模型。显然，按照上面的定义，自由主义模型并不是激励相容的，更接近于一种“劫富济贫”的平均化行为。

去年9月底，Ron Lavi等三位学者在论文《Redesigning Bitcoin‘s Fee Market》中提出了一种接近激励相容的虚拟资产费用设计——垄断价格机制（以下简称“MP机制”），今年11月，姚期智的Conflux团队从理论计算机科学的角度用严谨的数学证明支持MP机制可以作为“Virtual asset fee design candidate”（虚拟资产费用设计的备选方案）。下面我们介绍MP机制的核心内容。

垄断价格机制

“pay your bid”机制

当下多数区块链社区的主要参与方是矿工和用户。矿工对维护区块链网络安全起到关键的作用，矿工在出块奖励和手续费的经济激励下，负责打包交易的工作。

在现有的区块链社区费用设计中，用户支付的手续费是在一种公开可见情况下由用户自由报价确定的，论文中将之定义为“pay your bid” 机制，考虑到每个区块有容量限制（即打包到每个区块的交易数量有上限），该机制的痛点在于：

1. 在待转账数量较多时，矿工将交易的手续费按从大到小排序（按单位字节比较）后选择交易进行打包。用户为了让自己的交易尽快被矿工打包到区块，必须不断加高手续费，同时可能还得盯着时刻变化的报价以保证自己的价格能胜出，使得手续费被恶性竞价抬高，用户体验极差。而矿工可能在区块大小更小的情况下获得更多的收益（区块容量越小，交易被打包进区块的竞争越激烈）。

2. 区块容量太小导致转账拥堵可以通过扩大区块等方式来缓解，但扩大区块后又可能引发新的问题。在待转账数量较少时，区块容量没填满，用户发现自己的交易大概率会被打包，同时可以看见其他用户的报价，于是可以有恃无恐地不断压低自己的报价，导致矿工因得不到足够的收入而离场，降低区块链网络的安全性。

总而言之，“pay your bid” 机制下的用户会受到区块大小的影响而出现非诚实报价，导致费用设计不合理。R. Lavi等人提出的MP机制剔除了区块大小的影响，而且被证明是接近激励相容的。

MP机制

MP机制的一个前提是：假定用户希望他们的交易能尽快被打包在下一个区块内。

另外，为了简易推理流程，假设每笔交易占用区块的大小相同，直接比较每笔交易费用，推广到一般情况，用单位字节费用替代每笔交易费用即可。

MP机制规则：

1. 将交易池中的交易按费用从大到小排序，例如有6笔交易费用：（3，2，2，1，1，1）。

2. 矿工从最高费用的交易开始选取一组交易，按被选取交易组合中的最低出价收费。例如，选取前3笔（3，2，2），则对3笔交易收取费用 3 × 2 = 6；选取前4笔（3，2，2，1），则对4笔收取费用 4 × 1 = 4；

3. 假设在 n 笔已经排序的交易中选取了前 k 笔交易，相应费用为 b_k，则 R = k × b_k 即矿工的收入，假设 k = k* 时，R 取最大值 Rmax，该最大值 Rmax 被称为垄断收入（monopolistic revenue），第 k* 个费用 b_k* 即为垄断价格（monopolistic price）。当垄断收入对应多个 k* 时，取 k* 的最大值（保证收入不变，尽可能打包更多交易）。在上面的例子中，可以计算出，当 k = 3 或 6 时，均能获得垄断收入Rmax = 6，根据规则，垄断价格取 k = 6 对应的费用，即 1，6个交易都被打包进区块。

4. MP机制隐含条件：选取交易数量上限由区块大小决定；矿工只考虑眼前利益。

如果每个用户都按自己能接受的最高费用诚实报价，那么MP机制可以在满足用户意愿的情况下使矿工获得最高收入。同时，论文验证了虽然用户可以在某些情况下通过隐匿诚实报价（bid shading）或多重策略报价（multiple strategic bids）来获得更大的利益，但当用户数量足够大时，两种策略给他们带来的额外利益接近于0。在这样的情况下，自利用户为避免自己的交易不被打包的风险，会进行诚实报价，同时矿工获得最佳收入。所以MP机制是接近激励相容的。

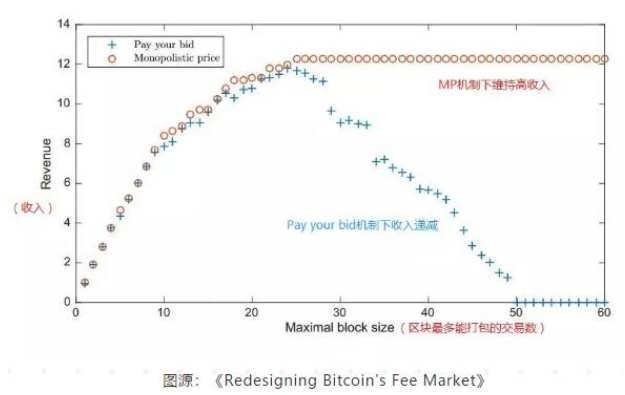
上图展示了通过模拟对比两种费用设计机制下矿工的收入随区块大小变化曲线。假设区块最多能打包的交易数为L，矿工的手续费从［0，1］区间随机取值。在“pay your bid”机制下，考虑极端情况（用户都是自利的），用户看到别人的出价后将自己的竞价调低到从大到小排序后第L+1个报价，而MP机制则按照相应规则计算垄断收入。

可见在区块容量较大时，“pay your bid”机制会迫使矿工接受手续费低于合理价位的交易直到填满区块。而相反地，不管区块容量大小如何，MP机制保证了矿工每次按达到垄断收入的计算规则选取一定数量的交易，用户恶意压低手续费将面临其交易不能及时被打包到区块的风险。

用户的自利博弈

MP机制中，用户存在两种情况可以钻空子让自己的交易被打包的同时节省手续费：

隐匿诚实报价（bid shading）

用户可以通过隐匿自己可接受的最高报价而谋求利益。

举例：假设有n个用户，他们各自的最高报价均为v=1，如果所有用户都诚实报价，即b=v=1，那么垄断收入为R=n，k*=n，垄断价格为p=1。这个时候，有个用户i发现，他/她可以策略性地降低报价为bi=1-1/n，这样前n-1个交易和前n个交易的垄断收入均为n-1，根据定义，最终垄断价格为用户i的策略价格1-1/n，他/她可以节约一点手续费同时保证自己的交易被打包。

为了使自己获得更多利益，用户隐匿自己的诚实报价而给出的策略价格（strategic price）是保证该用户的交易能被打包的最低价格，定义如下：

也就是：对于除用户i以外给定的一组交易（b1，。..，bi-1，bi+1，。..，bn），找到一个价格bi，使bi按从大到小顺序插入到该组交易中后计算得到的垄断价格小于等于bi，所有可能bi的组合中最小值即为策略价格。

如何计算策略价格？

假设有一组报价（9，8，7，6，5，4，3，2，1），对第一位用户而言，排除他的报价9，矿工在剩余序列依次取交易组合的收入如下表所示：

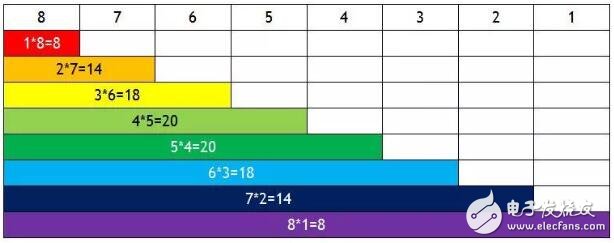
可见如果没有第一位用户的交易，垄断价格是4，垄断收入是20，而第一位用户想要保证自己的交易被矿工打包，他的策略价格应该是20/7，插入2和3之间，仍然会被打包进区块。

如下图所示的模拟结果显示，对于交易池价格在某个区间均匀分布的情况而言，高于平均水平的出价用户往往能找到低于其诚实价格的策略价格（Winning players），而低于平均水平的出价用户往往会得到一个高于其诚实价格的策略价格（Loosing players），且策略价格大部分集中在某一值附近。当然，交易池内的手续费价格分布不同会导致不同的结果。

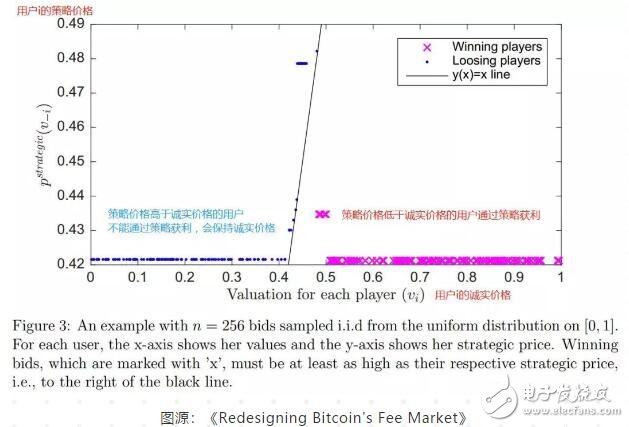
那么，为什么说MP机制是接近激励相容的呢？有了策略价格和诚实垄断价格（用户诚实报价情况下得到的垄断价格），我们可以计算出一个用户靠策略节省手续费的折扣率delta，论文中对折扣率的最大值delta_max在用户数量趋近无穷大时的极限等于0进行了证明。

这里我们不讨论证明过程，只举一个具体的例子让读者有更直观的印象：

1. 假设交易池内的交易取值为1或2，那么报价为1的交易明显更多，垄断价格为1，策略价格为1-1/n，最大折扣率为delta_max=1/n，当n趋近于无穷大时，delta_max趋近于0；

2. 当报价为2的交易明显更多时，垄断价格为2，策略价格为2（1-1/k*），其中，k*=pn是报价为2的交易数量（p为交易池中报价为2的概率），最大折扣率为delta_max=1/k*。当n趋近于无穷大时，delta_max趋近于0；

3. 当报价为2的交易数量比报价为1的交易数量多1笔时，例如（2，2，2，2，1，1，1），垄断价格为2，策略价格为1-1/n，delta_max=0.5+1/（2n）。当n趋近于无穷大时，delta_max趋近于0.5。然而，出现这种情况的概率类同于随机行走n步之后回到0点的概率，在n趋近于无穷大时极限为0。

多重策略报价（multiple strategic bids）

另一种策略是将同一笔交易拆分成多笔交易投入交易池，例如，交易池内有4笔交易，手续费排列为（5，2，1，1），如果用户都进行诚实出价，那么垄断价格为5，第二笔交易开始将不被打包。此时，发起第二笔交易的用户可以通过拆分策略，提交两笔手续费为1的交易，使手续费排列变为（5，1，1，1，1），这时垄断价格变为1，5笔交易都将被打包。