

正弦波形的相量图定义和相量代数方程教程
描述
Phasor Diagrams是表示两个或多个交替量之间的幅度和方向关系的图形方式
相同频率的正弦波形之间可能存在相位差,表示角度差两个正弦波形。此外,术语“引导”和“滞后”以及“同相”和“异相”通常用于表示一个波形与另一个波形的关系,其中广义正弦表达式如下: (t) = A m sin(ωt±Φ)表示时域形式的正弦曲线。
但是当以这种方式以数学方式呈现,有时难以可视化两个或更多个正弦波形之间的这种角度或相量差异。克服这个问题的一种方法是使用Phasor Diagrams以空间或相量域形式在图形上表示正弦曲线,这是通过旋转矢量法实现的。
基本上旋转矢量,简称为“相量”是一个缩放线,其长度表示一个具有幅度(“峰值幅度”)和方向(“相位”)的交流量,它在“冻结”时某个时间点。
相量是一个在一端有箭头的矢量,它部分表示矢量的最大值( V 或 I )部分是旋转矢量的结束。
通常,假设矢量在一端围绕一个称为“原点”的固定零点旋转,而箭头表示数量,在每个循环的一个完整旋转的角速度(ω)下沿逆时针方向方向自由旋转。矢量的这种逆时针旋转被认为是正旋转。同样,顺时针旋转被认为是负旋转。
虽然术语矢量和相量都用于描述旋转线本身具有幅度和方向,但两者之间的主要区别是矢量幅度是正弦波的“峰值”,而相量幅度是正弦波的“rms值”。在这两种情况下,相位角和方向保持不变。
任何时刻交替量的相位都可以用相量图表示,因此相量图可以被认为是“时间函数” ”。可以通过以ω=2π的角速度旋转的单个矢量来构造完整的正弦波,其中 f 是波形的频率。然后Phasor是一个同时具有“幅度”和“方向”的数量。
通常,在构建相量图时,总是假设正弦波的角速度为:ω,单位为rad / sec。考虑下面的相量图。
正弦波形的相量图

作为单向量以逆时针方向旋转,其尖端 A 将旋转一整圈 360 o 或2π代表一个完整的循环。如果其移动尖端的长度以不同的角度间隔在时间上传递到如上所示的曲线图,则将在零时间从左侧开始绘制正弦波形。沿水平轴的每个位置表示从零时间开始经过的时间, t = 0 。当向量是水平的时,向量的尖端代表0 o ,180 o 和360 o 的角度。
同样,当矢量的尖端是垂直的时,它代表90 o 或π/ 2 + Am ) >和负峰值,( -Am )在270 o 或3π/ 2 。然后,波形的时间轴表示相量移动的角度或弧度。因此我们可以说相量代表旋转矢量的缩放电压或电流值,它在某个时间点“冻结”( t ),在上面的例子中,这是一个角度有时当我们分析交替波形时,我们可能需要知道相量的位置,代表特定时刻的交替量,特别是当我们想要的时候比较同一轴上的两个不同波形。例如,电压和电流。我们在上面的波形中假设波形在时间 t = 0 时开始,相应的相位角为度或弧度。
但是如果第二个波形从左边开始或者在这个零点的右边或者我们想用相量表示法表示两个波形之间的关系,那么我们需要考虑波形的这个相位差Φ。请考虑上一个相位差异教程中的下图。
正弦波形的相位差
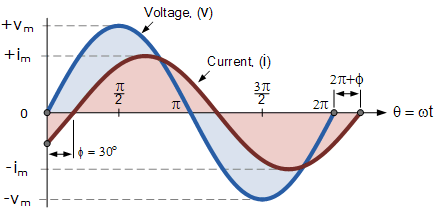
定义这两个正弦量的广义数学表达式将是写作:
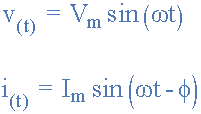
当前, i 滞后于电压, v 按角度Φ,在上面的例子中,这是 30 o 。因此,表示两个正弦量的两个相量之间的差异是角度Φ,并且得到的相量图将是。
正弦波形的相量图
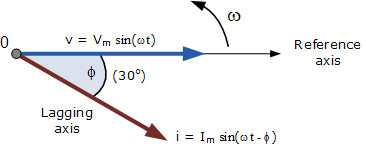
相对于水平轴上的时间零点( t = 0 )绘制相量图。相量的长度与绘制相量图的瞬间电压,(V)和电流(I)的值成比例。电流相量滞后于角度Φ,因为两个相量如前所述沿逆时针方向旋转,因此角度Φ也以相同的逆时针方向测量。

但是,如果波形在时间冻结, t = 30 o ,相应的相量图看起来就像右边所示。由于两个波形具有相同的频率,电流相量再次落后于电压相量。
然而,由于电流波形现在正在越过水平零轴线,我们可以使用电流相量作为我们的新参考,并且正确地说电压相量“引导”电流相量的角度Φ。无论哪种方式,一个相量被指定为参考相量,并且所有其他相量将相对于该参考超前或滞后。
相量加法
有时,在研究正弦曲线时,必须将两个交替的波形加在一起,例如在AC串联威廉希尔官方网站 中,它们彼此不同相。如果它们是同相的,则没有相移,那么它们可以以与DC值相同的方式加在一起,以找到两个矢量的代数和。例如,如果分别为50伏和25伏的两个电压“同相”,它们将相加或相加形成一个75伏(50 + 25)的电压。
然而,如果,它们不是同相的,也就是说,它们没有相同的方向或起点,那么需要考虑它们之间的相位角,因此使用相量图将它们加在一起以确定它们的结果相量或矢量和使用平行四边形法。
考虑两个交流电压, V 1 具有20伏的峰值电压, V 2 具有30伏的峰值电压,其中 V 1 通过 60 o 引导 V 2 。两个电压的总电压 V T 可以通过首先绘制表示两个矢量的相量图然后构建其中两个边是其中的平行四边形来找到。电压, V 1 和 V 2 ,如下所示。
Phasor增加两个相量
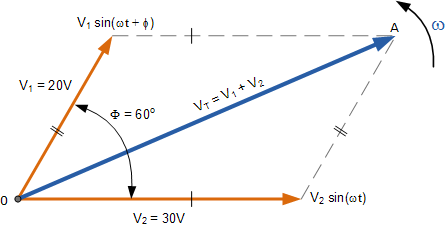
通过绘制两个相量来缩放到方格纸上,它们的相量和 V 1 + V 2 可以通过测量对角线的长度,称为“合成r-向量”,从零点到施工线的交叉点 0-A 。这种图形方法的缺点是在绘制相量以进行缩放时非常耗时。
此外,虽然这种图形方法给出的答案对于大多数目的来说足够准确,但如果不是这样,它可能会产生错误。准确或正确地绘制。然后,通过分析方法确保始终获得正确答案的一种方法。
在数学上我们可以通过首先找到它们的“垂直”和“水平”方向将两个电压加在一起,然后由此我们可以计算得到的“r向量”的“垂直”和“水平”分量,<跨度> V <子>Ť 。这种使用余弦和正弦规则来找到该结果值的分析方法通常称为矩形形式。
在矩形形式中,相量被分成实部, x 和虚部, y 形成广义表达式 Z = x±jy 。 (我们将在下一个教程中更详细地讨论这个问题)。然后,这给出了一个表示正弦电压的幅度和相位的数学表达式:
复杂正弦波的定义
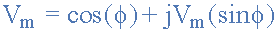
因此,使用先前的通用表达式添加两个向量 A 和 B 如下:
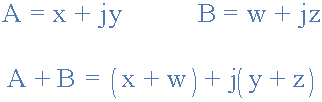
使用矩形形式的相量加法
电压, V 2 沿参考方向的30伏电压点水平零轴,然后它有一个水平分量但没有垂直分量如下。
•水平分量 = 30 cos 0 o = 30伏
•垂直分量 = 30 sin 0 o = 0伏
这给了我们电压 V 2 的矩形表达式: 30 + j0
电压, V 1 的20伏电压, V 2 60 o ,然后我t具有如下水平和垂直分量。
•水平分量 = 20 cos 60 o = 20 x 0.5 = 10伏
•垂直分量 = 20 sin 60 o = 20 x 0.866 = 17.32伏
然后给出us电压 V 1 的矩形表达式: 10 + j17.32
合成电压, V T 是通过将水平和垂直分量加在一起得到的,如下所示。
V Horizontal = V 1 和 V 2 的实部之和= 30 + 10 = 40伏
V 垂直 = V 1的虚部之和 和 V 2 = / 0 + 17.32 = 17.32伏特
现在已经找到了实数和虚数值电压 V T 仅通过使用确定对于90 o 三角形,g毕达哥拉斯定理如下。

然后得到的相量图将是:
V T的结果值

相量减法
相量减法与上述矩形加法非常相似,不同之处在于此时矢量差是 V 两个电压之间平行四边形的另一个对角线1 和 V 2 ,如图所示。
两个相量的矢量减法

这次不是将水平和垂直分量“加”在一起,而是将它们带走,减法。
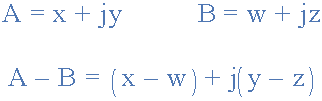
三相相量图
以前我们只看过单个多匝线圈旋转的单相交流波形在磁场中。但是,如果三个相同的线圈匝数相同的线圈在相同的转子轴上以120 o 的电角度放置,则会产生三相电压供应。
平衡三相电压源由三个单独的正弦电压组成,这些电压在幅度和频率上都相等,但彼此之间的电相位相差正好120 o 。
标准做法是将三个阶段的颜色编码为红色,黄色和蓝色,以识别每个阶段红相作为参考相。三相电源的正常旋转顺序为红色,然后是黄色,然后是蓝色,( R , Y , B )。
与上面的单相相量一样,代表三相系统的相量也以逆时针方向旋转围绕中心点的方向,如标记为ω的箭头所示,单位为rad / s。三相平衡星形或三角形连接系统的相量如下所示。
三相相量图

相电压的大小都相等,但相位角只有不同。线圈的三个绕组在点处连接在一起,a 1 ,b 1 和c 1 以产生三个共同的中性连接个别阶段。然后,如果将红相作为参考相,则可以相对于公共中性点定义每个单独的相电压。
三相电压方程

如果红色相电压 V RN 被视为前面所述的参考电压,那么相序将是 R - Y - B 所以黄相中的电压滞后 V RN 120 o ,蓝相中的电压也滞后 V YN 也是120 o 。但我们也可以说蓝相电压 V BN 导致红相电压 V RN 120 o 。
关于三相系统的最后一点。由于三个单独的正弦电压在120 o 之间具有固定的关系,因此它们被称为“平衡”,因此,在一组平衡的三相电压中,它们的相量和总是为零: V a + V b + V c = 0
Phasor Diagram Summary
然后总结本教程关于Phasor Diagrams的一些内容。
最简单的说,相量图是旋转矢量在水平轴上的投影,代表横轴瞬时值。由于可以绘制相量图来表示任何时刻,因此任何角度,交替量的参考相量总是沿正x轴方向绘制。
矢量,相量和相量图仅适用于正弦交流交流量。
>相量图可用于在任何时刻表示两个或多个固定的正弦量。
通常,参考相量沿着水平轴并在该时刻绘制其他相量。所有相量均以水平零轴为参考。
可绘制相量图以表示两个以上的正弦曲线。它们可以是电压,电流或其他一些交替量,但它们的频率必须相同。
所有相量都沿逆时针方向旋转。参考相量之前的所有相量都称为“前导”,而参考相量后面的所有相量都称为“滞后”。
通常,相量的长度代表均方根
由于矢量的速度不同,不同频率的正弦曲线不能在相同的相量图上表示,这是正弦曲线的数值而不是其最大值。 。在任何时刻,它们之间的相位角都会不同。
可以将两个或多个向量相加或相减,成为单个向量,称为a结果向量。
向量的水平边等于实数或“x”向量。矢量的垂直边等于虚数或“y”矢量。合成的直角三角形的斜边相当于“r”向量。
在三相平衡系统中,每个单独的相量移位120 o 。
在下一篇关于 AC Theory 的教程中,我们将把正弦波形表示为矩形形式的复数,Polar形式和指数形式。
- 相关推荐
- 正弦波
- 教程
- 波形
- 交流威廉希尔官方网站
- 相量图
-
电源技术之正弦波形(二)2020-09-18 0
-
三相正弦波脉宽调制(SPWM)信号发生器SM20012010-01-10 1360
-
带失控保护的正弦波移相威廉希尔官方网站2008-03-23 1147
-
使用阻极射线管的高次代数方程式解题机2008-05-01 1165
-
正弦稳态交流威廉希尔官方网站 相量的研究2008-09-22 24660
-
三相正弦波脉宽调制(SPWM)信号发生器SM20012009-07-08 5349
-
三相T/6正弦波形发生器威廉希尔官方网站 图2009-07-17 2406
-
正弦稳态威廉希尔官方网站 的相量模型的详细资料说明2019-04-15 1020
-
利用相量图求解正弦稳态威廉希尔官方网站2023-03-09 2041
-
什么是微分代数方程?Matlab求解微分代数方程2023-07-19 2348
全部0条评论

快来发表一下你的评论吧 !

