

Batch Norm的工作原理2018年被MIT的研究人员推翻
描述
Batch Normalization在2015年被谷歌提出,因为能够加速训练及减少学习率的敏感度而被广泛使用。
但论文中对Batch Norm工作原理的解释在2018年被MIT的研究人员推翻,虽然这篇论文在2018年就已经提出了,但是我相信还有很多人和我一样,在网上看相关博客及paper时,大部分内容还是论文提出前写下的。
现在DL逐渐变成了实验科学,一般在发现性能上的提升后去分析其产生的原因,但这片论文的思想很好,从数据、公式等一系列角度去推理,分析出来了为什么batch Normalization能work。
batch Normalization的提出
抛开Norm,我们在做特征工程时,经常会将输入进行归一化,否则如果某个特征数特别大(比如说一个特征是0-1,一个特征是0-1000),那第二个特征很有可能会对整个模型参数造成很大的影响。或者说,当训练集数据的分布不一致时,例如前一个输入的各特征范围是0-1,后一个是0-100,网络的训练效果也不会很好。
所以,就像很多人说的一样,我们希望在deep learn中,整个网络中流过的数据都是独立同分布的。
为什么需要独立同分布?
我觉得这事可以从两方面去解释,
一方面我们希望对训练集进行训练后,在测试集上能够发挥很好的性能。那么我们就需要保证训练集和测试集是来自同一个空间,准确来说,是符合同一分布,这对同分布提出了要求。此外,在虽然数据来自同一个空间,但我们并不希望所有数据都聚集在空间中的某一小撮,而是希望所有数据对于整个空间来说都具有一定代表性,因此在采样的过程中我们希望是独立得去采样所有的数据。
另一方面,其实是从另一个角度来阐述上一段话,如果数据之间不是同分布的,比如说样本1所有的特征都处于0-1之间,样本2处于10-100,那么网络的参数其实很难去同时迎合两类分布的数据。
batch Normalization做了什么?
上面讲到了数据在最初进来的时候,都希望是独立同分布的。但是batch Normalization的作者觉得不够,应该在deep learning中的每层都进行一次处理,保证在每层都是同分布。
他是这么想的:假设网络有n层,网络正在训练,还没有收敛。这时候x1被输入,经过了第一层,但是第一层还没有学到正确的weight,所以经过weight的矩阵乘法后,第二层的数会不会很乱?会不会第二层有些节点值是个位数,有些节点值蹦到好几百?细想一下,确实挺有可能啊,内部的参数都是随机初始化的,那蹦啥结果确实不好说啊。然后恐怖的事情来了,第二层这些乱蹦的数,又输到了第三层,那第三层的输入就是乱蹦的数,输出当然好不了,以此类推。
所以主要产生了两个问题:
1.所以在前面的网络没有收敛的时候,后面的网络其实并学不到什么。一栋大楼底部都是晃的,那上面也好不了。所以必须要等前面的层收敛后,后面层的训练才有效果。
2.因为一般来说网络内部每层都需要加一层激活来增加非线性化嘛,那么如果值比较大,它通过激活以后在S曲线上会比较接近0或1,梯度很小,收敛会很慢。
所以batch Normalization就想在每层都加一个norm进行标准化,让每层的数分布相同,变成均值0,方差1的标准分布。高斯分布的标准化公式就是下面式子中括号内的部分。值减去均值再除以方差,能够得到均值为0,方差为1的标准正态分布。至于γ和β,是需要学习的两个参数,γ对数据的方差再进行一个缩放,β对数据的均值产生一个偏移。
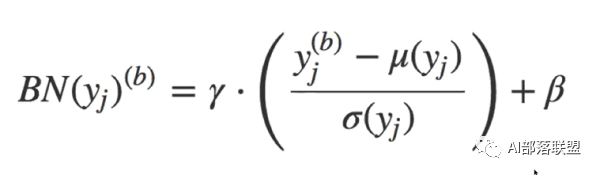
为什么归一化成均值0,方差1后,还要再修改方差和均值?那归一化还有意义吗?
这是因为我们并不能保证这层网络学到的特征是什么,如果简单的归一化,很有可能会被破坏。比如说S型激活函数,如果这层学到的特征在S的顶端那块,那么我们做归一化以后,强行把特征带到了S的中间位置,特征就被破坏了。要注意γ和β是被训练的参数,且每层都不一样,所以针对每一层的实际情况,它会去尝试恢复这层网络所学到的特征。
结果
使用VGG网路,CIFAR10数据集(下图),可以看到与不加相比:
1.训练前期的准确率要高,也就是收敛更快。
2.减少对learning rate的敏感度,图二在lr=0.5时,不加norm的网络直接震荡了,但加nrom的仍然表现良好。
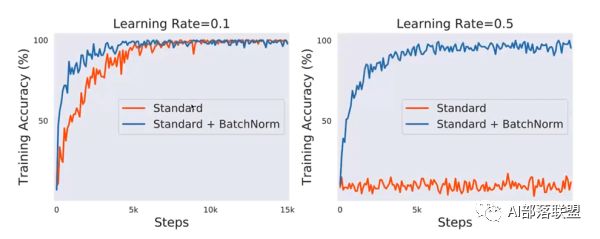
所以batch normalization其实原理不是很高深,只是在每层都加了一个标准化,使得数据同分布,再对其方差和均值进行一个变换以恢复该层捕捉到的特征。最后产生了两大改变,首先收敛更快,其次对lr的敏感度降低。
那网络内每层进行一个归一化,为啥这么简单的一个思想,一直没有被运用呢?是researcher想不到吗?
我相信有很多researcher都尝试过将各层都重新标准化,但我相信最后的效果一定不太好,因为很多特征重新修改为均值0方差1后,特征的信息会被丢失。所以作者理论的突破性在归一化以后又使用γ和β重新将数据的分布进行了一个修改,以此来找回丢失的特征,当然了,只要让这两个参数能够自学习就可以了。
其实现在大部分博客沿用的解释,都是上面这种。包括我之前一直也认为是这样。
但是《How Does Batch Normalizetion Help Optimization》这篇论文认为,使用norm后的网络收敛更快,lr敏感度更低是对的,但不是因为论文里说的这种原因,而是因为每层的标准化使得最后的loss函数变成了一个光滑的曲面而造成的最后性能提优。下面来阐述一下思想:
batch Normalization 解释的反驳
实验测试
MIT的研究人员并没有在论文的一开始就提出了自己的解释。而是说,如果原作者说的是对的,那我们就先按照原作者的思路去验证一下(因为涉及两篇paper,所以本文将batch normalization的提出者写为原作者,How Does Batch Normalizetion Help Optimization的作者写为来自MIT的研究人员):
原作者认为是因为网络中各层都标准化后使得分布相同,因此造成的性能提优。
来自MIT的研究人员做了三个实验作为对比:不适使用norm的普通网络、使用nrom的普通网络及添加噪音的Norm网络。
Norm网络添加噪音是考虑到原作者认为是同分布造成的性能提优。那么来自MIT的研究人员就在Norm网络的基础上,给各层再手动添加噪音,这样使得第三个网络虽然使用了norm,但每层的分布已经被打乱,不再满足同分布的情况。
下图中的实验结果表明,即使nrom网络添加了噪音,但性能仍然和添加norm的网络差不多。
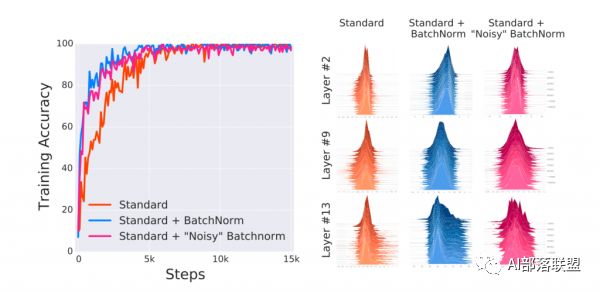
那么最后造成性能提升的原因,肯定不是数据同分布这一解释,也就是说原作者给出的解释是错的,一定有其他的原因。
batch Normalization新解释的直观理解
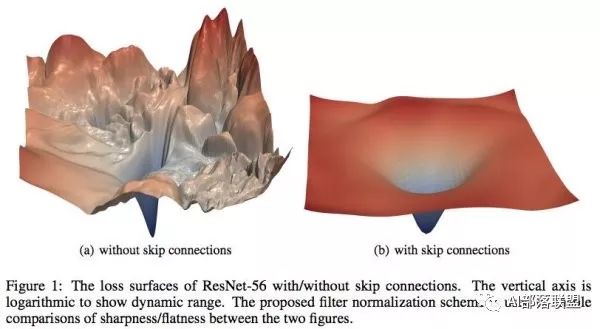
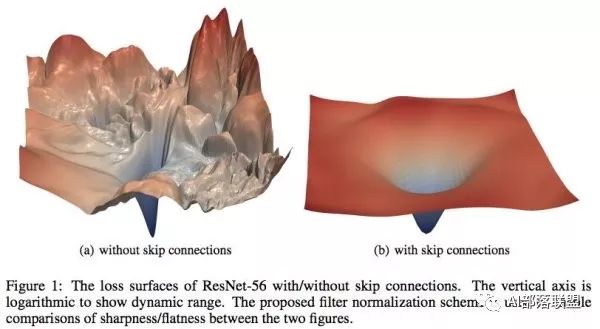
在基础的学习中,我们都知道在设计loss的时候希望loss函数是光滑的,这样我们可以很顺利地使用梯度下降来更新参数并找到一个较优点。但很多时候loss并不是我们想象中的那么美好。比如说下图,左边和右边都是loss函数,但是左边的loss虽然连续,但并不光滑。在梯度下降过程中很难保证下降的有效性和快速性,此外也很容易陷入局部最优解。而右边的图虽然在四个顶点出也有局部最优解,但总体上来说还是非常理想的一个loss。
MIT的研究人员认为batch normalization的有效性在于它将左边的原始loss转变成了右边的loss,造成了上文提到的两种结果:
1.收敛速度变。
2.对学习率的设置不再那么敏感。
分析
MIT的研究员定义了两个函数:
第一个是loss的值的计算,就是下面第一个公式,内部的loss是当前的loss,随后对loss求导,再乘以学习率,x是内部的参数,对参数进行一个更新,随后将新参数放入loss函数中,计算当前loss的值。别看这个公式看起来有点绕,实际上就是求当前的loss值。
第二个公式是计算loss的梯度差,也可以看成loss的二次求导吧(我感觉)。
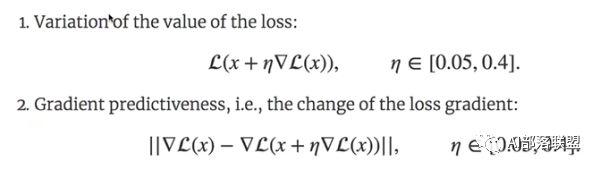
论文中之所以提出这两个公式,是为了得到两个量。
第一个公式可以得到训练过程中的loss,那么把每一个step的loss都拿出来绘制成一条曲线,该曲线可以认为是loss的波动情况。我认为如果一个loss函数本身是比较光滑的,那么第一个公式求出来的loss值并不会有一个比较大的浮动。
第二个量是计算loss的梯度差,它可以认为山坡在沿着下降的方向走时,方向改变是否会较大。也就是说,一个比较好的loss函数,在每一个step中,loss所得到的梯度应该是不会浮动太大的。就好像从山上往下走,我们向下的方向一般都不会在瞬间改变太大,而不是说往下平滑地走着走着(loss梯度稳定),突然前面是个悬崖(loss梯度骤变),而应该是有个台阶(loss梯度平滑改变)。
MIT研究人员将使用norm和普通的网络对这两个量进行了对比:
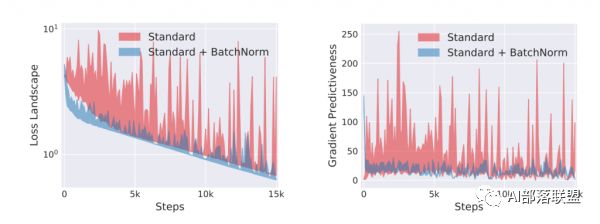
可以看到不使用norm的网络(红色),loss的梯度差浮动均较大。而使用了norm的网络(蓝色)浮动很小。也就从侧面印证了普通网络的loss比较趋向于左图。而使用了norm的,loss趋向右图。
上面这两个公式其实就是整篇论文的核心,MIT的研究人烟也正是基于这两个量从而对原文进行了反驳。
1.在论文中使用了L-Lipschitz常数来定量loss的光滑程度(也就是公式1干的事),限制了loss的光滑程度,(以下定义来自百度百科)
L-Lipschitz:直觉上,利普希茨连续函数限制了函数改变的速度,符合利普希茨条件的函数的斜率,必小于一个称为利普希茨常数的实数(该常数依函数而定)。对于在实数集的子集的函数
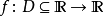
,若存在常数K,使得
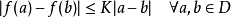
,则称 f 符合利普希茨条件,对于f 最小的常数K 称为 f 的利普希茨常数。
我个人觉得就是换了种说法,就是限制loss的一阶导数要小于常数k。一阶导数在曲线上表现的是斜率必须小于一个值,也就是说斜率不能过大。在这一条件的限制下,loss的面哪怕下降,也是很缓的。
2.论文使用了另一个更强的光滑条件来限制:β-smoothness(也就是公式2干的事)。
β-smoothness限制了就是loss斜率的斜率(可以简单看成斜率差)不能超过一定值。
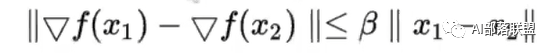
我认为这本质上其实就是二阶求导。对二阶求导后的结果进行了一个限制,使得函数在二阶条件下仍然是一个较为平滑、不会大幅度突变的函数。
也正是因为使用了batch norm的网络,它的loss从原先的原始凹凸不平状态变成了一个能满足L-Lipschitz及β-smoothness两个强条件的原因,使得bath norm能够work。
总结
原作者提出了batch norm,并造成了两个结果:
1.收敛更快。
2.对learning rate的敏感度更低(也就是说lr的设置是否合理不会很大程度地影响最终结果)。
并且认为网络中每层都进行了一次同分布,是造成结果的主要原因。
MIT研究员根据这一思路,将使用norm的网络随机添加高斯噪声,使得网络在添加了norm的同时又去除了norm所带来的同分布效果,但结果显示优势仍然存在,因此对原作者的解释进行了反驳。
随后MIT研究人员使用了loss的一阶信息和二阶信息进行了评估,发现使用了norm以后的loss在一阶和二阶上都具有很好的性质,由此推断nrom之所以能产生效果,不是原作者提出的解释,而是因为norm直接作用了loss函数,将loss函数变成了一个一阶、二阶均平滑的函数。
-
日研究人员新发现:光纤也能变身太阳能电池2009-04-14 0
-
MIT 认为现有的电动车就能取代美国 87%的燃油车,里程焦虑被过分夸大2016-08-19 0
-
泰克仪器助力研究人员首次通过太赫兹复用器实现超高速数据传输2018-08-31 0
-
福州大学研究人员撰文质子交换膜燃料电池工作原理2017-12-22 11297
-
研究人员探究大脑如何控制主动传感2018-12-29 3003
-
MIT研究人员开发出新型“光子”芯片2019-06-12 3926
-
59%的中国籍AI研究人员隶属美国研究机构2019-06-20 8380
-
Facebook向研究人员发布友谊数据2020-04-22 3348
-
研究人员已经使用机器学习来开发血液测试2020-05-21 1980
-
AI研究人员如何应对透明AI2020-07-14 1912
-
苹果启动安全研究设备计划 为安全研究人员提供越狱iPhone2020-07-23 641
-
研究人员开发了一种基于深度学习的智能算法2020-09-10 2293
-
batch normalization时的一些缺陷2020-11-03 3162
-
MIT研究人员提出了一种制造软气动执行器的新方法2022-05-06 1679
-
MIT/三星研究人员利用活体拉曼光谱直接观察葡萄糖指纹图谱2024-06-05 396
全部0条评论

快来发表一下你的评论吧 !

