CMOS器件的等比例缩小发展趋势,导致了栅等效氧化层厚度、栅长度和栅面积都急剧减小。对于常规体MOSFET,当氧化层厚度<2 nm时,大量载流子以不同机制通过栅介质形成显著的栅极漏电流。栅极漏电流不仅能产生于沟道区域,而且能在栅极与源/漏的交叠区域产生。穿越栅氧化层的电流增加了威廉希尔官方网站
的泄漏电流,从而增加了威廉希尔官方网站
的静态功耗,同时也影响MOS器件的导通特性,甚至导致器件特性不正常。栅漏电流增加成为器件尺寸缩减的主要限制因素之一。
栅氧化层越薄,栅漏电流越大,工艺偏差也越大。栅漏电流噪声一方面影响器件性能,另一方面可用于栅介质质量表征,因此由栅介质击穿和隧穿引起的栅电流涨落为人们广泛关注。为了更好地描述和解释栅电流涨落对MOS器件性能的影响,迫切需要建立栅漏电流噪声精确模型。MOS器件噪声的研究,始于60年代,至今已有大量研究报道文献。而栅漏电流大的MOS器件噪声特性的研究仍是现今研究中活跃的课题。尤其当MOS-FET缩减至直接隧穿尺度(<3 nm)时,栅漏电流噪声模型显得尤为重要,并可为MOSFET可靠性表征和器件设计提供依据。文中基于MOSFET栅氧击穿效应和隧穿效应,总结了栅漏电流噪声特性,归纳了4种栅漏电流噪声模型,并对各种模型的特性和局限性进行了分析。
1 栅漏电流噪声模型
(1)超薄栅氧隧穿漏电流低频噪声模型。
模型基于泊松方程与薛定谔方程自洽数值求解,采用一维近似描述了器件的静态特性,模型考虑了栅材料多晶硅耗尽效应和量子力学效应。在描述超薄氧化层的栅漏时,同时考虑了势垒透射和界面反射,电子透射系数表达式为
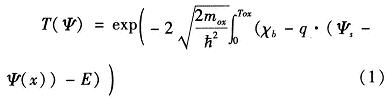
其中,χb为势垒高度,ψ(y)为位置y处的电势,E为隧穿电子能级。
总栅隧穿电流为
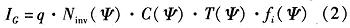
其中,Ninv(ψ)为反型层电荷,C(ψ)为取决于界面反射的修正系数,fi(ψ)为频率因子。
氧化层内部的缺陷对栅漏电流涨落的贡献,已在格林表达式中考虑和体现。这种近似允许摈弃等效平带电压涨落的假设,由此得到的栅电流涨落谱密度为

其中,
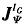
为与静电势ψ(y)相关的栅电流,IG的雅可比矩阵,Gψ(x,x1)为氧化层x1处的单位电荷在氧化层x处的电势ψ(x)的格林函数。
氧化层中的陷阱可发射载流子至沟道或从沟道中俘获载流子。对于近二氧化硅/多晶硅界面捕获的载流子,若其再发射,进入多晶硅栅,应用朗之万方程,假定产生几率不受再发射过程的影响,则单位体积内占据陷阱数量涨落的谱密度为

其中,
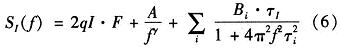
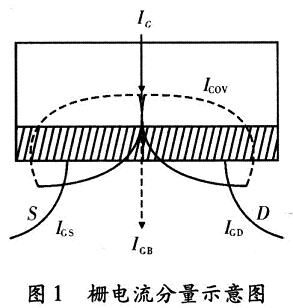
由BSIM4提出的简易MOS模型的栅极电流分量模型
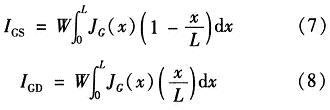
其中,JG是栅极电流密度,L是沟道长度,W是沟道宽度,x是沿沟道的位置(源极处x=0,漏极处x=L),IGS和IGD是栅极电流的栅/源和栅/漏分量。通过线性化栅电流密度与位置的关系,简化这些等价噪声电流分析表达式,所得的总栅极电流噪声表达式为
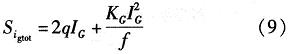
常数KG可通过低频噪声实验测试获得,IG可通过直流测试得到。
(4)栅电流噪声电容等效电荷涨落模型。
FET沟道中的热噪声电压涨落导致了沟道静电势分布的涨落。沟道成为MOS电容的一块平板,栅电容之间的电压涨落引起电荷涨落,将电荷涨落等效于栅电流涨落。在Van Der Ziel对JFET诱生栅噪声的早期研究之后,Shoji建立了栅隧穿效应的MOSFET模型,即是将MOS沟道作为动态分布式的RC传输线。器件沟道位置x处跨越△x的电压涨落驱动两处传输线:一处是从x=0展伸至x=x,另一处从x=x展伸至x=L。栅电流涨落作为相应的漏一侧电流涨落和源一侧电流涨落之间的差异估算得出。在极端复杂的计算中保留Bessel函数解的首要条件,于器件饱和条件下,估算得出了栅电流涨落噪声频谱密度解析表达式为
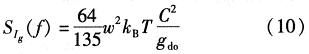
2 模型分析与探讨
实验表明,超薄栅氧MOSFET栅电流噪声呈现出闪烁噪声和白噪声成分,测试曲线表明白噪声接近于散粒噪声(2qIG)。对于小面积(W×L=0.3×10 μm2)器件,1/f噪声成分几乎为栅电流IG的二次函数,栅电流噪声频谱密度SIG(f)与栅电流IG存在幂率关系,即SIG(f)∝IGγ。
超薄栅氧隧穿漏电流低频噪声模型适用于超薄栅氧化层MOSFET低频段噪声特性表征,与等效栅氧厚度为1.2 nm栅电流噪声测试结果的对比,验证了其正确性。通过模型与实验噪声测试结果及器件模拟的对比,可用于提取慢氧化层陷阱密度分布。
唯象模型利用势垒高度涨落和源于二维电子气沟道的栅极泄漏电流的洛仑兹调制散粒噪声,来解释过剩噪声特征。低频和高频范围内,测量值和仿真值均有良好的一致性。模型将过剩噪声解释成1/f‘伊噪声和洛仑兹调制散粒噪声之和,能够准确预测超薄栅氧化层的MOS晶体管的过剩噪声性质并适于在威廉希尔官方网站
仿真中使用。
栅电流分量噪声模型,模拟结果与低漏偏置下的1.5 nm栅氧厚度p-MOSFET的数值模拟结果和实验数据一致。该模型适用于纳米级MOSFET,仅限于描述由栅隧穿效应引起的栅漏电流涨落。模型两待定参数都可通过实验获得,可方便计算不同偏置下的点频噪声幅值。等效电容电荷涨落模型中,栅电流通过栅阻抗产生的电压涨落经由器件跨导在沟道处得到证实。该模型仅适用于器件饱和条件下,由于忽略了衬底效应,诱生衬底电流和沟道中的高场效应,其适用性和精确度均不高。
3 结束语
虽然已经提出多种小尺寸MOSFET栅电流噪声模型,但各模型均有局限性。等效电容电荷涨落模型局限性很大,超薄栅氧隧穿漏电流低频噪声模型可用于精确描述低频噪声特性。唯象模型和栅电流分量噪声模型则主要取决于栅隧穿效应。从噪声特性看低频段噪声功率谱近似为栅电流的二次函数,在低温环境白噪声主要成分为散粒噪声。这些噪声模型主要针对隧穿机制,全面描述各种隧穿机制引起的栅漏电流模型还有待研究。
CMOS器件的等比例缩小发展趋势,导致了栅等效氧化层厚度、栅长度和栅面积都急剧减小。对于常规体MOSFET,当氧化层厚度<2 nm时,大量载流子以不同机制通过栅介质形成显著的栅极漏电流。栅极漏电流不仅能产生于沟道区域,而且能在栅极与源/漏的交叠区域产生。穿越栅氧化层的电流增加了威廉希尔官方网站
的泄漏电流,从而增加了威廉希尔官方网站
的静态功耗,同时也影响MOS器件的导通特性,甚至导致器件特性不正常。栅漏电流增加成为器件尺寸缩减的主要限制因素之一。
栅氧化层越薄,栅漏电流越大,工艺偏差也越大。栅漏电流噪声一方面影响器件性能,另一方面可用于栅介质质量表征,因此由栅介质击穿和隧穿引起的栅电流涨落为人们广泛关注。为了更好地描述和解释栅电流涨落对MOS器件性能的影响,迫切需要建立栅漏电流噪声精确模型。MOS器件噪声的研究,始于60年代,至今已有大量研究报道文献。而栅漏电流大的MOS器件噪声特性的研究仍是现今研究中活跃的课题。尤其当MOS-FET缩减至直接隧穿尺度(<3 nm)时,栅漏电流噪声模型显得尤为重要,并可为MOSFET可靠性表征和器件设计提供依据。文中基于MOSFET栅氧击穿效应和隧穿效应,总结了栅漏电流噪声特性,归纳了4种栅漏电流噪声模型,并对各种模型的特性和局限性进行了分析。
1 栅漏电流噪声模型
(1)超薄栅氧隧穿漏电流低频噪声模型。
模型基于泊松方程与薛定谔方程自洽数值求解,采用一维近似描述了器件的静态特性,模型考虑了栅材料多晶硅耗尽效应和量子力学效应。在描述超薄氧化层的栅漏时,同时考虑了势垒透射和界面反射,电子透射系数表达式为
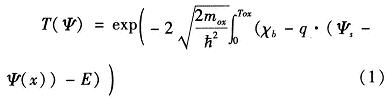
其中,χb为势垒高度,ψ(y)为位置y处的电势,E为隧穿电子能级。
总栅隧穿电流为
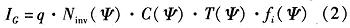
其中,Ninv(ψ)为反型层电荷,C(ψ)为取决于界面反射的修正系数,fi(ψ)为频率因子。
氧化层内部的缺陷对栅漏电流涨落的贡献,已在格林表达式中考虑和体现。这种近似允许摈弃等效平带电压涨落的假设,由此得到的栅电流涨落谱密度为

其中,
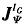
为与静电势ψ(y)相关的栅电流,IG的雅可比矩阵,Gψ(x,x1)为氧化层x1处的单位电荷在氧化层x处的电势ψ(x)的格林函数。
氧化层中的陷阱可发射载流子至沟道或从沟道中俘获载流子。对于近二氧化硅/多晶硅界面捕获的载流子,若其再发射,进入多晶硅栅,应用朗之万方程,假定产生几率不受再发射过程的影响,则单位体积内占据陷阱数量涨落的谱密度为

其中,
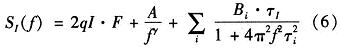

由BSIM4提出的简易MOS模型的栅极电流分量模型
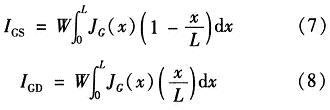
其中,JG是栅极电流密度,L是沟道长度,W是沟道宽度,x是沿沟道的位置(源极处x=0,漏极处x=L),IGS和IGD是栅极电流的栅/源和栅/漏分量。通过线性化栅电流密度与位置的关系,简化这些等价噪声电流分析表达式,所得的总栅极电流噪声表达式为
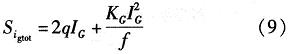
常数KG可通过低频噪声实验测试获得,IG可通过直流测试得到。
(4)栅电流噪声电容等效电荷涨落模型。
FET沟道中的热噪声电压涨落导致了沟道静电势分布的涨落。沟道成为MOS电容的一块平板,栅电容之间的电压涨落引起电荷涨落,将电荷涨落等效于栅电流涨落。在Van Der Ziel对JFET诱生栅噪声的早期研究之后,Shoji建立了栅隧穿效应的MOSFET模型,即是将MOS沟道作为动态分布式的RC传输线。器件沟道位置x处跨越△x的电压涨落驱动两处传输线:一处是从x=0展伸至x=x,另一处从x=x展伸至x=L。栅电流涨落作为相应的漏一侧电流涨落和源一侧电流涨落之间的差异估算得出。在极端复杂的计算中保留Bessel函数解的首要条件,于器件饱和条件下,估算得出了栅电流涨落噪声频谱密度解析表达式为
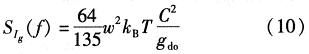
2 模型分析与探讨
实验表明,超薄栅氧MOSFET栅电流噪声呈现出闪烁噪声和白噪声成分,测试曲线表明白噪声接近于散粒噪声(2qIG)。对于小面积(W×L=0.3×10 μm2)器件,1/f噪声成分几乎为栅电流IG的二次函数,栅电流噪声频谱密度SIG(f)与栅电流IG存在幂率关系,即SIG(f)∝IGγ。
超薄栅氧隧穿漏电流低频噪声模型适用于超薄栅氧化层MOSFET低频段噪声特性表征,与等效栅氧厚度为1.2 nm栅电流噪声测试结果的对比,验证了其正确性。通过模型与实验噪声测试结果及器件模拟的对比,可用于提取慢氧化层陷阱密度分布。
唯象模型利用势垒高度涨落和源于二维电子气沟道的栅极泄漏电流的洛仑兹调制散粒噪声,来解释过剩噪声特征。低频和高频范围内,测量值和仿真值均有良好的一致性。模型将过剩噪声解释成1/f‘伊噪声和洛仑兹调制散粒噪声之和,能够准确预测超薄栅氧化层的MOS晶体管的过剩噪声性质并适于在威廉希尔官方网站
仿真中使用。
栅电流分量噪声模型,模拟结果与低漏偏置下的1.5 nm栅氧厚度p-MOSFET的数值模拟结果和实验数据一致。该模型适用于纳米级MOSFET,仅限于描述由栅隧穿效应引起的栅漏电流涨落。模型两待定参数都可通过实验获得,可方便计算不同偏置下的点频噪声幅值。等效电容电荷涨落模型中,栅电流通过栅阻抗产生的电压涨落经由器件跨导在沟道处得到证实。该模型仅适用于器件饱和条件下,由于忽略了衬底效应,诱生衬底电流和沟道中的高场效应,其适用性和精确度均不高。
3 结束语
虽然已经提出多种小尺寸MOSFET栅电流噪声模型,但各模型均有局限性。等效电容电荷涨落模型局限性很大,超薄栅氧隧穿漏电流低频噪声模型可用于精确描述低频噪声特性。唯象模型和栅电流分量噪声模型则主要取决于栅隧穿效应。从噪声特性看低频段噪声功率谱近似为栅电流的二次函数,在低温环境白噪声主要成分为散粒噪声。这些噪声模型主要针对隧穿机制,全面描述各种隧穿机制引起的栅漏电流模型还有待研究。

 举报
举报

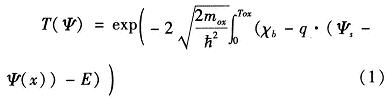


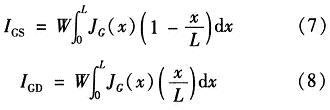

 举报
举报

