

结构光相位展开技术的基本原理是什么
测量仪表
描述
结构光三维形貌测量方法越来越多地应用于逆向工程、航空航天、生物医学、文物保护等领域。相位展开作为结构光三维测量中的一个关键环节对测量精度、速度和可靠性起着决定性作用。
据麦姆斯咨询报道,近期,河北工业大学机械工程学院和赫德斯菲尔德大学精密技术中心的科研团队在《红外与激光工程》期刊上发表了以“面向结构光三维测量的相位展开技术综述(特邀)”为主题的文章。该文章第一作者和通讯作者为张宗华教授,主要从事光学检测、三维数字成像和造型、条纹自动分析等方面的研究工作。
本文综述了相位展开技术的研究进展:介绍了相位展开技术的基本原理;将现有的相位展开技术进行分类并详细综述各类技术的研究现状以及优缺点和适用性分析;对不同技术的几种主要特点进行了比较和分析;总结分析了相位展开技术的未来研究趋势和可能的研究方向。
相位基本原理
相移法以其操作简单、高效率、高精度等优点广泛应用于光学测量领域。通常,经典的三维形貌测量步骤包括:条纹投影、相机采集变形条纹、条纹分析、相位展开、系统标定、点云计算、三维形貌重建。其中条纹分析的目的是得到包裹相位,位于区间(−π,π]呈现锯齿形状的相位信息。得到包裹相位常用的条纹分析方法是相移法、小波变换法和傅里叶变换法,其中相移法具有计算结果准确、可靠性高和对环境和噪声不敏感等优点。Zuo等已经对各类相移算法做了较为全面的比较。文中涉及到的包裹相位部分,统一采用相移方法求解。相移方法把投影的条纹图案在一个周期内均匀移动N步(N≥3),每次移动2π/N,根据这N幅变形条纹图案来求得折叠相位ϕ(x,y)。相位展开的意义是将由反正切函数计算得到的截断相位恢复为连续分布的相位,用于后续的三维形貌恢复。
相位展开技术分类
下面对以下4种相位展开技术的进展进行详细介绍:1)时间相位展开技术;2)空间相位展开技术;3)基于深度学习的相位展开技术;4)其他相位展开技术。
时间相位展开技术
时间相位展开是按照时间顺序将一系列不同频率的条纹投影到被测物体上,相机捕获被测物体表面的变形条纹。根据捕获的一系列按照时间顺序排列的变形条纹图案,可以将每个像素点的相位根据时间序列的条纹图组相对独立地完成相位展开,得到连续的相位分布。由于时间相位展开与相邻相位无关,展开相对独立,因此时间相位展开也可以用于计算非连续表面的相位值。
自Huntley和Saldner提出时间相位展开技术以来,研究者们针对相位展开的效率和准确性这一问题进行了大量研究,使得时间相位展开技术快速发展。1993年,Huntley和Saldner提出时间相位展开技术,有效克服了相位展开过程中的误差传播,使条纹图案的空间频率随时间呈线性序列(条纹周期数为:1,2,3,⋯,N0,N0表示最大投影条纹周期数)。算法实现像素独立展开,且在时域中进行,可以将相位误差限制在低信噪比区域内。此外,相位不连续的区域也可以实现正确展开,用于测量非连续物体表面。该技术存在的问题是相位图建立缓慢,多适用于静态测量,不适用于较快的动态测量。之后,Huntley和Saldner将时间相位展开技术用于改进的测量系统,简化了标定过程,使得时间相位展开技术可以更有效的应用于实际测量中。
该技术的主要优点是:可有效测量高度不连续的被测物体,测量误差与使用的条纹图数量成反比。阴影对图像的影响与传统投影条纹的影响程度相同,但是相位误差被限制在阴影区域内,不会传播,影响具有良好信噪比的区域。为了简化Huntley和Saldner所提出的技术,Zhao等提出一种新方法,主要原理是基于用于相位展开的两个相位图像具有不同的精度,且条纹阶次由较低精度的相位图像赋值。该方法每个点的相位展开也都是独立完成,且计算相位展开的方法可以自动生成相位图,而无需定位条纹中心或分配条纹阶数。被测物体的非连续性以及噪声问题对该方法影响较小,但是可否用于欠采样的问题未得到验证。
Huntley和Saldner比较分析了已有时间相位展开计算方法的性能,同样为了减少投影图像数量和简化计算量,提出了一种指数序列相位展开技术,使条纹图案的空间频率随时间呈指数变化(条纹周期数为:1, 2, 4,⋯, N0),即所需投影图案数目与总相位范围呈对数变化关系,而非线性变化。证明了该技术可以有效的抑制噪声的影响,对噪声较为不敏感。由于高度测量误差与总相位范围成反比关系,因此误差随着展开图像的数量增加呈指数下降,可有效降低测量误差。该技术不仅为相位展开实现最大化可靠性和最小化计算量提供了一种选择,也在一定程度上提升了测量精度。但是对于相位展开的速度和准确度而言,仍存在一定的提升空间。针对时间相位展开的精度提升和速度加快问题,Huntley和Saldner提出了一种反向指数序列的相位展开技术(条纹周期数为:N0, N0-1, N0−2,⋯, N0/2)。
该技术不仅提高了信噪比,而且通过线性最小二乘法提高了相位展开技术的测量精度(提高s1/2倍,其中s是投影条纹的总数)。在不考虑测量时间的情况,可实现较高的测量精度。对于具有深斜坡或局部不连续的物体表面,通常不能满足香农抽样定理,为了恢复局部陡峭曲面片的形状,针对采样问题和时间效率问题,Peng等提出一种以递归方式实现的增强时间展开方法。采用递归方法使得重建曲面的分辨率提高,从而实现多分辨率重建,提高对被测物体细节测量的准确度。
不同的时间相位展开技术具有不同的优缺点,适用于不同的测量场景和物体,Huntley和Saldner所提出的不同时间相位展开技术可以总结为:线性序列相位展开技术、指数序列相位展开技术和反向指数序列相位展开技术。其中线性序列所需图像的数量最多,因此所需图像最多,测量速度最慢且计算量最大;后两种指数序列利用了相位和投影条纹数之间的指数关系,与线性序列相比,所需图像总数减少,一定程度上提高了测量效率。
为实现精度更高、误差更小、抗噪性更好和更具有时间效率的相位展开,更好地解决相位展开过程中的误差传播效应,更有效地用于非连续表面的测量,逐渐发展出越来越多不同形式的时间相位展开技术。时间相位展开的发展过程中形成的方法可总结分为四类:基于格雷码的相位展开、多频相位展开、多波长相位展开和基于数论的相位展开。以下对四种方法的基本原理和发展过程进行详细的介绍说明。
基于格雷码的相位展开
格雷码(Gray code)最早于19世纪40年代被提出。由于格雷码固有的编码优势,Inokuchi等将其应用到结构光三维形貌测量的编码技术中。格雷码采用的是二值编码,但是格雷码的特殊性在于相邻数字编码之间只差一位,最大数与最小数之间也只相差一位,因此出差率低,用于编码解码可以使得误差降低到最小。
格雷码图案通过投影仪投射到被测物体表面,相机捕获经过被测物体表面调制后的格雷码图案,结合系统标定结果,解码即可实现被测表面的三维重建。编码和解码过程如图1所示。
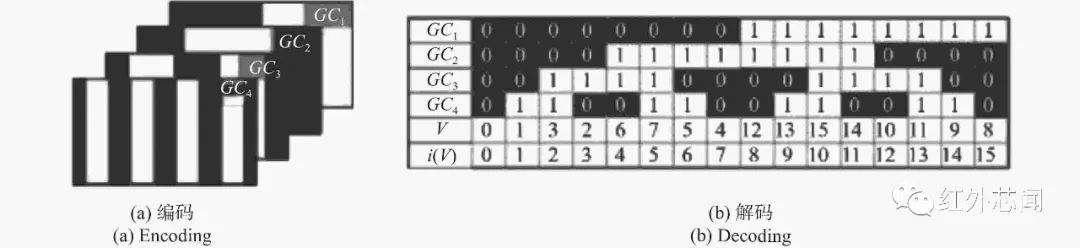
图1 格雷码编码和解码过程
根据格雷码的编码特性,可以实现在解码过程中唯一定位到每一个条纹,可以根据提取条纹的边界和提取条纹的中心确定。相对而言,条纹边界的准确提取是影响解码准确度的主要问题。随着对格雷码方法的深入研究和不断发展,多种格雷码相关的相位展开技术被提出,可将基于格雷码的相位展开(PU-GC)分为:二值格雷码方法、多灰度格雷码方法、格雷码结合相移方法和基于格雷码编码原理的其他方法,这四类方法都可以归类为在结构光三维测量中常用的格雷码方法。
为了提高时间相位展开的效率,Sansoni等提出了一种将相移与格雷码相结合的结构光三维测量方法。格雷码技术被用来测量不连续表面,而相移算法可以测量较为精细的表面细节,使得该系统具有较好的线性度,提高了与分辨率和测量范围相关的测量性能。在基于格雷码结合相移技术的三维形貌测量中,可以对复杂或不连续表面的物体进行测量。但是由于被测表面反射率不均匀、背景光强度、噪声以及散焦的影响,相邻两个二值的边界,尤其是黑白转换边界的界限不明显,不易实现清晰的分割,从而导致解码相位顺序出错。针对上述问题,2012年Zhang等提出了互补格雷码的编码方法。该方法需要一个额外的格雷码,形成互补格雷码图案,使得转换边界错开,保证了相位展开的可靠性和正确性,有效解决了边缘模糊导致的相位展开错误问题。
该方法使图像二值化和相位展开过程变得简单有效,但存在的缺点是需要投影和捕获额外的格雷码图案,降低测量效率从而影响测量速度。同样为了解决格雷码边界的边缘模糊问题,Zheng等提出了一种自校正格雷码的相位展开方法。该方法无需额外的条纹图案,解决了Zhang所提方法存在的问题。在校正过程中,相位展开可以充分利用包裹相位中的信息,限制相位跳变的搜索范围,整个搜索过程只对相位跳变的部分进行校正。因此在搜索过程中省去了不必要的时间浪费。此外,该方法对噪声影响敏感性较低。
格雷码方法在实际测量中,捕获的格雷码图案不再是二值图案,这导致在存在大量像素处易出现相位展开错误。为了更有效地消除相位展开误差,Zheng等提出了一种自适应中值滤波器,用于解决相移轮廓术与格雷码图案投影相结合的相位展开误差问题。该方法首先检测错误的像素;然后逐渐增大过滤器尺寸,直至获得较好的效果,可以最大程度地防止边缘问题。与传统中值滤波器相比,该方法可有效的去除错误像素,具有一定的优越性。但存在的问题是错误像素的检测过程较为耗时,影响测量效率。此外,该方法是检测跳变误差并补偿展开相位,属于后校正展开相位,适用于静态、缓慢变化、误差区域较小的场景,对于运动物体的动态场景等存在较大误差区域的情况则难以校正。
相移算法与格雷码结合的测量方法具有高鲁棒性和抗噪声能力,因此得到了广泛的应用。在实际测量场景中,由于投影仪的散焦、物体的运动以及物体表面反射率的不均匀性,产生的级次边沿误码问题会造成相位展开错误,因此该方法较为广泛的应用于静态场景的三维形貌测量,而较少用于动态高速测量场景中。如果可以在保证预先避免相位跳变误差的前提下,实现提升测量速度的同时解决投影仪非线性响应问题,则可以实现快速、可靠的三维形貌测量。逐渐发展起来的二元离焦技术突破了高速条纹投影和投影仪非线性响应的瓶颈,将其有效应用于准确快速的三维形貌测量。Wu等提出了一种循环互补格雷码方法,结合二元抖动技术和互补格雷码实现相位展开。在具有相同投影图案数的前提下,该方法与传统的灰度编码方法相比不仅扩展了相位测量范围,而且也提高了测量精度,可有效用于动态场景的高速三维测量。
但不足之处是测量深度范围存在一定的限制。为了使格雷码结合相移的方法可以更有效的用于高速测量,Wu等又提出了一种移动格雷码方法。该方法可以有效消除由反射率不均匀、环境光变化和投影仪散焦引起的大部分相位解包裹误差。移动格雷码编码方法可以避免相位展开在码字边缘的剩余误差。该方法也无需额外投影和采集条纹图案。陆丽莲等提出了一种基于错位格雷码的三维形貌测量方法,无需任何附加图案即可避免级次边沿误码问题,并有效提升了测量精度。
基于格雷码的方法用于动态高速测量的主要限制因素就是编码效率低和边界误差问题。针对这两类问题,提出了不同的相位展开方法。一方面针对边界误差问题,为了实现更高速高效的三维测量,Wu等提出了一种分区相位展开方法。其中,三相位展开可以避免主要由散焦和运动引起的码字边界跳跃误差。对于高速应用,使用较少数量的条纹图案可以减少运动诱发的伪影,时间重叠编码方法则可以提高编码效率,将每组中的投影图案数目从7个减少到4个。
结合三相位展开和时间重叠编码方法的优势,实现采用4幅投影图案重建具有强噪声动态场景条件下的被测物体三维形貌。该方法能够实现低信噪比高速动态场景的鲁棒、高效三维测量,保证了基于格雷码方法的高抗噪声能力,同时克服了跳转错误和低编码效率的缺点。但是该方法的局限性在于仅限于使用三步相移算法的相位提取,并且需要额外的参考折叠相位来分割条纹阶数区域。
Wu等将上述提出的方法应用于数字图像相关辅助的条纹投影轮廓术中,实现对纹理表面的高速三维形貌、位移和变形的测量。上述不同的测量方法虽然具有各自的局限性,但是都可以预先避免相位跳变误差,实现高速三维形貌测量。为了弥补以上方法的局限性,Wu等提出了一种格雷码复用的编码策略方法。该方法在原有的相位展开基础上建立另外两个交错的相位展开,并将条纹阶数的每个周期划分为3个部分,从而避免跳跃误差。同时,该方法具有一定的有效性和通用性,保证测量结果的情况下简化了测量过程。
另一方面针对编码效率提升问题,Zheng等提出了三灰度格雷码方法,通过增加格雷码的编码灰度级数,实现对格雷码编码效率的提升。对于条纹频率为f的正弦条纹,实现了格雷码编码图案数目从log2f减少至log3f。He等在Zheng三灰度编码方法的基础上,提出了四灰度编码方法,将格雷码编码图案数目从log3f减少至log4f,进一步提高了编码效率,加快了图像采集速度,扩展了在动态测量应用中的适用性。张昂等提出了一种三灰度编码相位展开方法,将投影条纹图案降低至5幅,包括3幅正弦相移条纹图像和两幅三灰度编码图像,在一定程度实现了测量速度的提升。之后,王浩然等提出了一种基于时间复用编码的方法,将重建一个三维结果所需的投影序列图案数目降至3幅,进一步提高了编码和重建效率。以上方法都是通过提高格雷码的编码效率实现减少投影和采集条纹图像的数量,从而提高测量速度。
基于格雷码的相位展开,具有很高的鲁棒性和抗噪声能力,受到系统非线性误差的影响较小。为了提高方法的效率,逐渐减少测量所需的条纹图案的数目,现有的多种基于格雷码的相位展开方法已经实现了可有效用于快速测量场景。
多频相位展开
多频相位展开(MFPU)主要原理是投射两组(或两组以上)不同频率的条纹图案,借助一个(或多个)具有不同频率的条纹图案的附加包裹相位图来实现相位展开,确定条纹阶数k。多频相移法最早提出时用于激光干涉测量,该方法也适用于条纹投影测量。
为了提高时间相位展开的精度,Li等提出了双频相位展开方法。将双频光栅投影到物体上,对高频和低频的大小做了一定的限定,其中高频比低频大几倍。该方法可实现高频相位的准确展开,且低频对测量高度的不连续性不敏感,使得该方法可更加有效地用于不连续性更大的物体表面测量。
多频相位展开中,如何合理有效地选择频率是决定相位展开准确度的关键问题。针对多频测量中最佳频率的选择问题,Towers等为多频干涉测量中的最佳频率选择引入了一个优化标准。该标准使得频率选择公式针对实现最大目标动态范围所需的最小频率数量进行了优化。所提出的频率选择方法会生成几何系列的波长,从而为干涉仪中使用的每个后续频率提供最大的动态范围。Towers根据优化标准提出了一种最佳三条纹选择方法,实现利用最少数量的投影条纹频率获得最大的测量范围。使用基于相干光纤的条纹投影仪,通过实验证明了最佳频率选择方法。仅使用3个频率,在整个视野中使用100个条纹,在条纹阶计算中实现了大于99.5%的可靠性。Zhang等将提出的最佳三条纹选择方法用于彩色条纹投影系统中,使用最佳三条纹选择方法实现每个像素独立计算绝对相位。该方法在采用3个频率的前提下可以实现精准的测量,且最佳三条纹选择方法的精度较普通的多频方法较高;投影图案数目相对较少;具有一定的抗噪性和鲁棒性。
双频相位展开对相位主值要求相对较高,因此易产生相位跳跃误差。兼顾测量时间效率和测量精度,选择3个频率的相位展开技术更为适用。
其中最佳三条纹选择方法,对于相同的工艺可靠性和相位噪声,最佳三条纹选择方法的测量范围是双频干涉测量的平方,比其他频率系列方法的测量范围更大。此外,最佳三条纹选择法所用的条纹图案数量较小,计算可靠性也较高。根据多频方法求得的各步结果如图2所示。
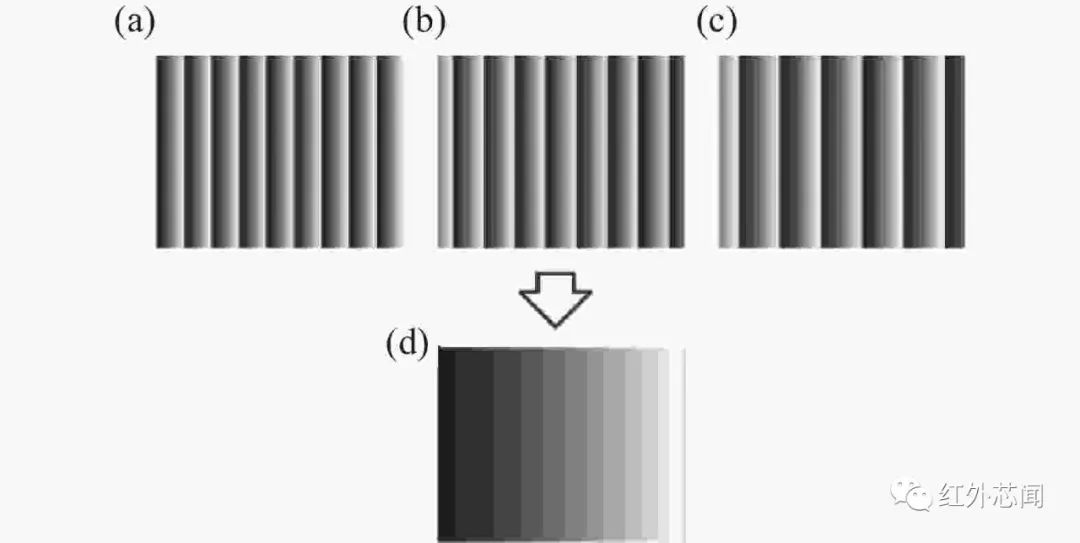
图2 最佳三条纹选择原理示意图。(a) 条纹频率为9的折叠相位;(b) 条纹频率为8的折叠相位;(c) 条纹频率为6的折叠相位;(d) 展开相位
多频相位展开具有测量精度高和相位展开可靠性高等优点,但是也存在投影条纹图案数量较多、所需测量时间较长导致的测量效率低等问题。针对以上问题研究者们提出了不同的改进方法,以实现在保证测量精度的同时提升多频相位展开技术的测量效率。针对已有的包括线性、拟合线性、拟合指数、拟合负指数等时间相位展开算法存在的使用投影条纹图案数目数量较大这一问题,研究者们相继提出不同的解决方法。徐珍华等提出了三频相位展开方法,投影三套条纹图即可获得展开相位。该方法有效降低了获取数据的数量并且一定程度上缩短了数据处理时间,提升了方法的测量效率。同样针对减少条纹图案的幅数,Liu等提出了一种新的双频方法,该图案将高频正弦分量与单位频率正弦分量相结合,其中高频分量用于生成稳健的相位信息,而单位频率分量用于减少相位展开过程的边界模糊问题。该方法可以使用更少的条纹图案数且获得更高质量的相位数据。为了获得兼具高效、高精度的相位展开方法,从完善三频展开法和外差法的角度,李璐璐等结合了三频展开法和外差法的优点提出了三频外差法。但是较三频展开法和外差法而言,不仅在精度和可靠性上表现较好,而且计算效率也得到了一定程度的提升。
从减小误差产生和修正误差的角度也可以实现减少相位误差提高测量精度的目的。陈玲等根据多频外差原理,提出了一种相位修正的方法,能够非常有效地去除相位误差。Zhang等针对采用多频条纹投影相位展开算法时可能会出现条纹阶差,进而导致相位展开误差问题,提出了一种校正由自由电子设备引起的相位误差方法。所提方法在一定程度上可以减少相位展开误差。针对误差问题,Zhang等定义了一个称为条纹阶次误差的参数,从理论上分析了可能导致条纹阶次误差的主要因素,提出了一种借助于条纹阶次误差优化选择条纹周期的方法,有助于优化选择条纹周期,并检测相位展开误差。该方法也可有效降低相位展开误差,提高测量精度。此外,赵文静等对几种多频时间相位展开引入了分块拟合的方法,先将整个相位场大小进行分块,然后再对每个子区域进行拟合,使得测量精度更高,相位误差也远小于以前采用的全场拟和法。为了消除现有多频外差原理相位展开结果存在的跳跃误差,陈松林等提出了相位展开过程中所需满足的一系列约束条件,对多频外差原理相位展开方法进行了改进,展开后的相位无需再次进行误差校正,相比现有方法时间效率提升30%以上。针对求解展开相位过程出现的跳变误差,韩玉等提出了一种基于多频外差的相位解包裹方法。该方法利用相邻像素点包裹相位求得的斜率和叠栅条纹的整数部分,判断是否存在跳跃性误差并进行修正,从而消除误差,得到了较为平滑的相位展开结果。
在提高多频相位展开的测量速度方面,多位研究者也做了相关的研究工作。Wang等提出一种双频二进制相移方法来测量跳动兔心脏的三维绝对形状。利用最佳脉宽调制技术生成高频条纹图和误差扩散抖动技术生成低频条纹图,通过采用双频移相,实现了跳动兔心脏的绝对相位恢复,并准确获得其三维形貌。但是该方法只实现了定性的测量。同样在提升多频相位展开测量速度问题上,Zhang等提出一种新的双频方法。该方法将高频正弦分量与单位频率正弦分量相结合,其中高频分量用于生成稳健的相位信息,而单位频率分量用于减少相位模糊。该方法一定程度上通过减少条纹图数目提升了测量速度,且配合实时处理数据算法,速度提升了约10倍。
对于多频相位展开而言,准确地选择最高条纹频率、相移步长和条纹图序列是实现准确、高效和可靠测量的关键问题。Zhang等提出了一种在多频时间相位展开同时确定最佳条纹频率、相移步长和图案序列的新方法。在保证精度的前提下,使用7个条纹图案即可实现三维形貌测量,有效实现了在保证精度的前提下提升测量效率问题。
多频相位展开在图案效率、精度和相位展开范围方面优于基于格雷码的相位展开。多频相位展开也具有较好的鲁棒性,但是在条纹图案数目上仍然有提升的空间。
多波长相位展开
多波长相位展开(MWPU)的参考相位是从两个相位函数的包裹差产生。以双波长为例,将已知的相位范围扩展到两个相近频率的拍频处合成等效波长。
多波长相位展开中双波长的抗噪能力较差,因此多使用3个及以上的波长用于相位展开。但是考虑所需条纹图案数目,因此多采用三波长的方法。多波长相位展开是通过外差技术将两个高频包裹相位图依次组合成低频相位图。与多频相位展开相比,在保持相位展开精度的前提下,多波长相位展开可以使用更少的条纹图案数目实现更快的相位展开。
基于数论的相位展开
基于数论的相位展开(NTPU)的主要理论支持是相对质数的性质。基于数论的相位展开具有简单、稳健的特点。但是由于频率或者波长的选择需要满足相对质数的性质,因此对于频率的选择具有一定的局限,且该方法的可靠性和抗噪性受低频影响较大。此外频率的限制也可能会导致测量范围存在一定的局限性。
空间相位展开技术
空间相位展开技术主要是以局部或全局优化的方式,通过比较相邻像素处的相位值,判断加减2π,以消除跳变得到绝对相位,且得到的两个相邻像素点的相位差值位于(−π,π]范围中。但是该技术应用于实际工程对象时存在一些问题,因为在相位展开过程中通常包含相位中的跳变,后序可能无法跨越这些存在的不连续性,使得相位展开误差从高噪声区域向低噪声区和其他区域累计传播,相位误差在图像中传播。虽然存在误差累积和误差区域扩大的问题,但是空间相位展开技术具有测量速度快的优势,因此在对于测量速度有较高要求的实际测量工作中也得到了广泛的应用。
空间相位展开技术根据算法原理大致分为:路径跟踪的局部算法和路径无关的全局算法。其中路径跟踪的局部算法包括质量引导相位展开法、枝切法;路径无关的全局算法包括无权和加权最小二乘法。
质量引导相位展开
质量引导相位展开(QGPU)因为具有高效、快速的优势,得到了广泛的研究。质量引导相位展开主要原理是以质量图为依据衡量包裹相位,按照所有相位点的质量高低排序从高到低完成相位展开。相位展开具体步骤分为两步:确定质量图;通过洪水填充算法进行相位展开。该方法可以有效限制低质量区域相位展开误差的传播。
1982年,Itoh最早提出空间相位展开条件和方法,但是受噪声影响较为严重。引导图质量好坏的判断一方面决定像素展开相位的正确性;另一方面也对相位展开的方向有影响。这些因素都会影响相位展开过程中的准确性、噪声干扰、误差扩散的问题,好的引导图质量对于相位展开的成功有着非常重要的影响,因此质量图质量高低的判别也是质量引导相位展开技术中的一个重要环节。Su等提出了一种基于可靠性引导参数映射的相位展开方法。该方法是根据参数映射引导相位展开路径,根据选择的一个或一组参数来识别相位数据的可靠性或相位展开的方向,如图3所示。可选择的参数包括:条纹图的调制度、条纹图的空间频率、相邻像素间的相位差、信噪比等。参数图是组合2个或3个参数生成,方法的核心就是先对参数图中参数值较高的像素进行相位展开。
该方法可以有效的将存在的相位展开误差限制在局部最小区域,具有很强的鲁棒性。Zhang等提出了由相位图梯度生成质量图的方法,多级阈值用于逐级展开相位。该方法虽然对原有的线扫描相位展开算法有所改进,但降低相位展开的计算速度。Fang等提出了一种基于可靠性评估的质量导引相位展开算法,以目标图像的强度作为衡量标准来评估包裹相位图中每个像素的可靠性,性能良好,且计算效率高。关于质量引导相位展开引导策略中的经典、两段和堆栈链三种策略而言,具有索引交织链表数据结构的经典指导策略具有准确度的优势,而堆栈链引导策略则速度更快。邻接列表在质量引导相位展开过程中起着非常重要的作用,索引交织链表是用于实现邻接列表的数据结构。Zhao等通过对质量引导相位展开方法中的索引交织链表提出了三项改进,实现减少计算量,提升相位展开速度。
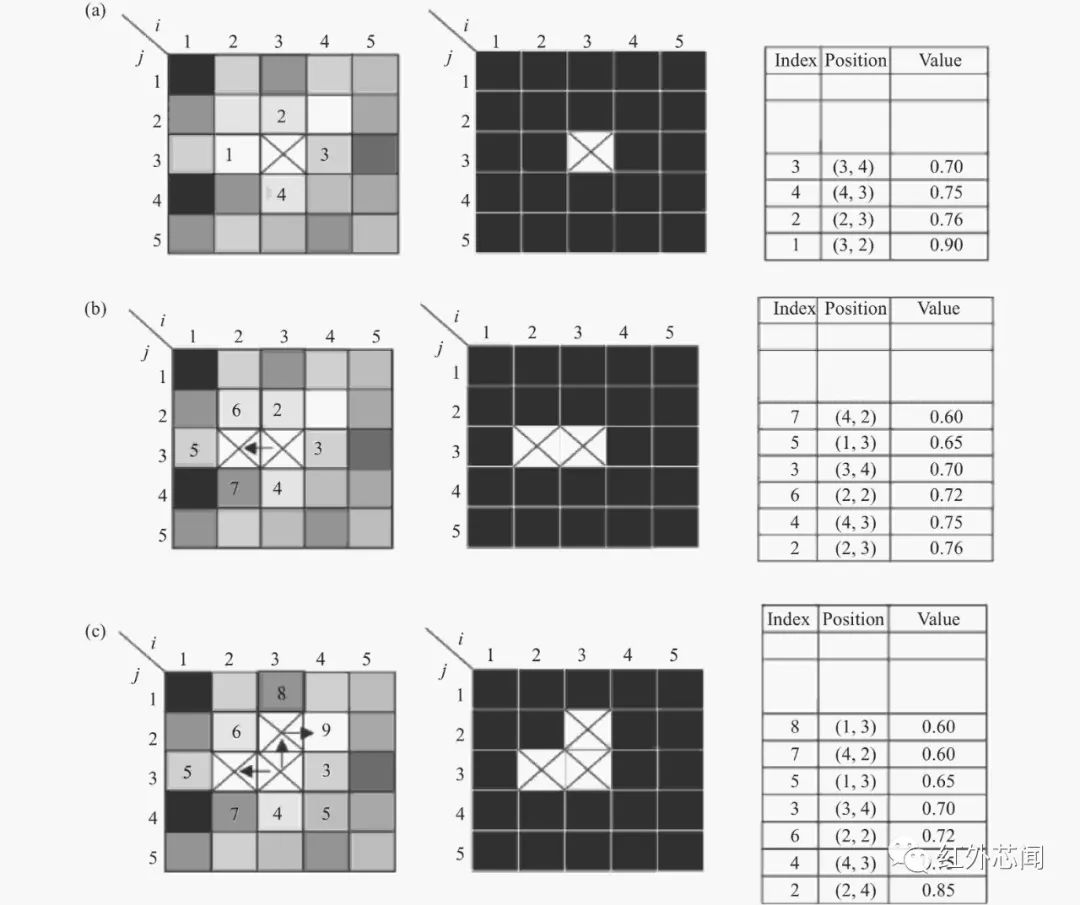
图3 基于定向平行映射的相位展开示例
质量引导相位展开,操作简单,速度较快,但是也不可避免地会存在因相位展开路径不正确而引起的相位误差。针对相位展开中如何减小误差获得精度更高的展开相位结果这一问题,不同研究者们提出了不同的解决方法。Li等利用小波变换系数在小波脊线位置的幅值映射来识别相位数据可靠性和相位展开路径的方法。该方法选择位于具有最高振幅值像素处的包裹相位作为相位展开的起点,较先展开具有较高振幅值的像素,所以相位展开的路径总是沿着振幅值最高的像素到振幅值最低的像素。该方法可以更好地实现将相位展开误差限制在局部最小区域。Qian等提出了一种加窗傅里叶滤波和质量引导相位展开方法。该方法将滤波后的振幅作为实际质量图,使得相位展开算法对包裹相位图中的低质量区域更具容错性。此外,该方法考虑了窗口大小的选择问题,使算法能够适应不同的相位抖动问题,较大的窗口有助于消除噪声和识别无效区域,而较小的窗口则有助于保留局部特征。Mostafavi提出了一种基于双三次插值法降低相位噪声的新滤波算法,双三次插值法与传统展开算法的结合提高了展开相位图的精度。
质量引导相位展开通常速度很快,并且对相位图中的噪声区域反应较为有效,但其鲁棒性和处理不连续性问题的能力具有一定限制。相关研究者试图解决空间相位展开无法用于非连续相位的展开问题,Arevalillo-Herraez等提出了一种基于剩余概念的质量度量方法,在质量引导方法中使用该度量值可以实现快速、稳健和成功的相位展开。但是相关研究仍处于初步试探,如果空间相位展开可稳健有效地用于非连续物体测量的相位恢复,将使得非连续物体的三维测量速度大大提高,可以解决一系列对测量速度有强烈要求的相关工业和工程问题。
枝切相位展开
枝切相位展开(BCPU)是另一种常用的路径相关类算法,主要步骤包括:1)识别残差点,识别图像中的所有残差点并标注其极性;2)构造枝切线,连接各个残差点并使枝切线上所有残差点极性值之和为零;3)相位展开,相位展开过程需绕过枝切线,残差点上的相位将根据其相邻己展开像素点的相位信息进行展开。相比于质量引导相位展开法,枝切法具有较好的抗噪性。枝切法通过构造枝切线并在相位展开时将误差避开,可有效避免误差传播。
枝切法(也称分支集算法、Goldstein算法或残差补偿算法)最早于1988年由Goldstein提出。该方法对展开相位过程中的噪声有较好的抑制作用,但是也存在一些问题,包括残差点密集处产生错误枝切线问题、枝切线不一定是全局最短问题和构造的枝切线形成闭环产生“孤岛效应”造成较大局部误差等问题。此外,该方法高度依赖于分支切割的位置,如果存在太多的噪声,则相位展开结果会存在许多错误。
针对Goldstein算法存在的上述问题,在后续的研究和发展中被不断改进和完善。Huntley等改进了Goldstein提出的枝切法,将抗噪性与计算效率相结合,通过放置障碍物或分支切割并给出一条不经过这些障碍物的展开路径,可以避免噪声通过损坏的点和区域传播。独立的展开路径可以实现唯一且准确的相位展开结果。针对算法计算速度慢的问题,Zheng等提出了搜索最短枝切线的新算法,基于随机搜索技术,实现找到最短的枝切线或其近似值的概率较大。与Goldstein算法相比,该算法在速度上实现一定提升。针对Goldstein算法中由于在残差点密集的区域建立的枝切线容易形成环路,使得一部分区域无法解包裹问题,张妍等改进了Goldstein算法,减小了枝切线的总长度,且有效避免了“孤岛效应”的形成。与Goldstein算法相比,该算法可有效减小误差。此外,Souza等提出了一个基于留数理论的相位展开方法,使用带移位相位跳跃的包裹相位图来平衡剩余极性的残差点,缩短处理时间,最多为Goldstein算法的1/10,提升了枝切法的计算效率,极大地促进了枝切法的发展。常丽等在Goldstein枝切法的基础上提出了优化改进方案,提出了一种基于禁忌搜索的改进枝切法。与Goldstein算法相比,枝切线长度减少了42%,速度提高了28%,有效地提升了测量速度。除了上述一系列针对Goldstein算法改进的方法以外,其他类方法被提出用于完善枝切法。Gdeisat等提出了一种增加包裹相位图中剩余数的方法,改善了相位展开结果的准确性。但是该方法非常耗时,涉及傅里叶变换的计算及其光谱成分的选择和移动。为了解决这一问题,Du等提出了一种简单的算法来增加包裹相位图中的剩余数,可以加快50%以上的计算时间,有效加快了测量速度。
基于深度学习的相位展开技术
总而言之,空间相位展开技术的计算效率较高,但是对严重噪声情况不具有鲁棒性,对于其中极个别的抗噪能力较强的算法又存在计算量大导致速度慢的问题。时间相位展开技术的精度较高也具有一定的鲁棒性和抗噪能力,但是由于是逐像素点在时间方向上实现相位展开,需要在时间顺序上投影多幅图案且无法实现利用单个包裹相位完成相位展开,因此不可避免地存在测量效率低、测量速度慢等问题。为了克服现有传统相位展开技术的缺点,从而可以实现在实际应用中以较短的时间获得较为准确的相位展开结果,研究者逐渐趋向于设计一种高效的体系结构用于相位展开过程,试图找到绝对相位和包裹相位的直接对应关系。最近发展起来的机器学习架构,特别是深度神经网络,可以有效地用于计算图像形成。
深度学习的优势也已经在光学计量得到了广泛的应用,于是将深度学习应用到相位展开被越来越多的提出。基于深度学习的相位展开技术主要针对提升测量效率和减少投影图案数目,从而体现了深度学习用于相位展开在速度上的优越性。最近,基于深度学习的方法被提出作为传统相位展开的替代方法,以提高速度和精度。
2018年,Spoorthi等将卷积神经网络用于相位展开,提出了一种基于深度卷积神经网络的相位展开模型,将相位展开问题转化为一个语义分割问题。该模型实现了利用深度卷积神经网络(DCNN)对相位进行展开,所提的框架通过自动生成大型标记数据的通用模拟过程避免DCNN标记训练数据这一复杂过程,有效减少了工作的复杂性,并且增加了结果的可靠性。之后,对上述所提方法进一步完善,Spoorthi等提出了一种基于DCNN的相位展开框架PhaseNet,通过完全卷积的结构来解决相位展开问题。
该框架对噪声具有鲁棒性,且计算速度快,但是由于网络的分类结果不够准确,因此需要增加后处理进行优化。此外,该框架目前只成功应用于仿真。为了进一步降低噪声因素的影响,解决低信噪比条件下相位展开错误问题,Spoorthi等提出了一种新的深度学习框架PhaseNet 2.0改进了现有的相位展开方法。该框架将相位展开问题表述为密集分类问题。相比于PhaseNet,该框架无需后处理,提升了数据处理速度且增强了对噪声的鲁棒性。
为了解决严重噪声影响和欠采样导致的相位展开错误问题,Wang等提出了一种相位类型对象的数据库生成方法和一步深度学习相位展开方法。该方法网络运行迅速,且可以自动运行,无需额外的预处理或后处理,具有较强的鲁棒性。针对噪声问题的解决,Zhang等将相位展开问题转化为多类分类问题,引入有效的分割网络来识别噪声。该方法可有效用于噪声问题,保证相位展开结果的可靠性。同样针对高噪声问题,Jiang等提出了一种基于深度卷积神经网络的相位展开方法,采用了具有噪声抑制和强大特征表示能力的DCNN架构DeepLabV3+。
该方法引入了深度神经网络,提供了一定的抗噪声能力。此外,针对严重高斯噪声的情况,Liang等提出了一种具有相同网络配置的两步训练过程,可以正确地展开具有严重高斯噪声的相位。对于非常高的噪声情况,Sumanth等提出了一种基于多任务学习的相位展开方法TriNet,用于在条纹投影中同时去噪和预测条纹阶数。该方法可以实现从高噪声边缘估计相位轮廓,对于存在非常高噪声和低信噪比情况,也可得到较好的相位展开结果。
由于空间相位展开原理是通过分析相邻像素的相位信息来展开相位,因此,上述基于空间相位展开采用的深度学习方法虽然可以实现快速可靠的相位展开,但是不能用于非连续物体表面的测量。时间相位展开技术原理则可用于测量具有非连续性表面的物体,将深度学习结合时间相位展开则可有效用于非连续物体表面的测量。Yin等为了提升时间相位展开的测量效率,提出了基于深度学习的时间相位展开,使用深度学习技术通过监督学习自动实现时间相位展开,原理如图4所示。
选用三步相移,则共需要6个投影图案,网络的输入数据是单周期和高频的两个包裹相位,输出为展开相位。与多频时间相位展开相比,该方法在不同类型的误差源(例如强度噪声、低条纹调制、投影仪非线性和运动伪影)影响的情况下,相位展开可靠性有所提高。
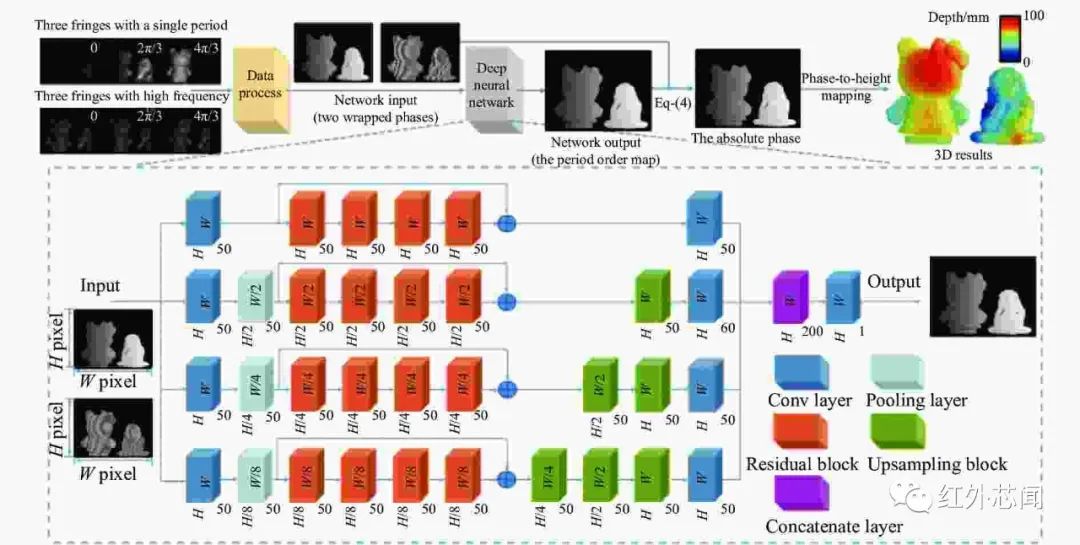
图4 Yin等所提方法的原理示意图
传统相位展开技术存在的一个较难克服的问题就是无法同时满足测量精度和所需图案数目最少的问题。时间相位展开技术的相位恢复精度较高,但是测量所需的投影图案数目较多,因此使得测量效率受到限制,无法用于高速高动态场景的测量。空间相位展开技术所需的投影图案数目较少,但是测量精度不高,因此无法用于一些对精度要求较高的测量场景。随着深度学习技术的发展,针对保证测量精度的前提实现减少投影图案数量的问题,研究者们提出不同的基于深度学习的相位展开技术。
为了使投影图案的数量最少并保持高精度,Yao等将深度学习应用于编码的条纹图案中,提出了一种多用途神经网络与基于编码的图案相结合恢复绝对相位的方法。该神经网络框架求解绝对相位仅采用3个条纹图案,即一个条纹图案和两个编码图案。该方法在保证测量具有较高的精度前提下实现了减少投影图案的数量。为了进一步减少所需的图案数目,Yao等提出了一种智能多编码深度学习方法(MCDL),实现从两个图案中求解高斜率绝对相位。该方法不仅减少了投影条纹图案的数量,且具有较高的精度和鲁棒性。对相位展开精度而言,条纹分析也至关重要,Feng等证明了可以训练深度神经网络来完成条纹分析,流程如图5(a)所示,其中图5(b)和(c)分别为CNN1和CNN2的示意图。较现有的方法对比,该方法可以提供条纹分析的框架,且无需人为干预。Feng等证明了贝叶斯卷积神经网络(BNN)可以训练,不仅可以从单个条纹图案中检索相位,还可以生成描述估计相位像素置信度的不确定性图,增加深度学习用于相位展开的可靠性和有效性。
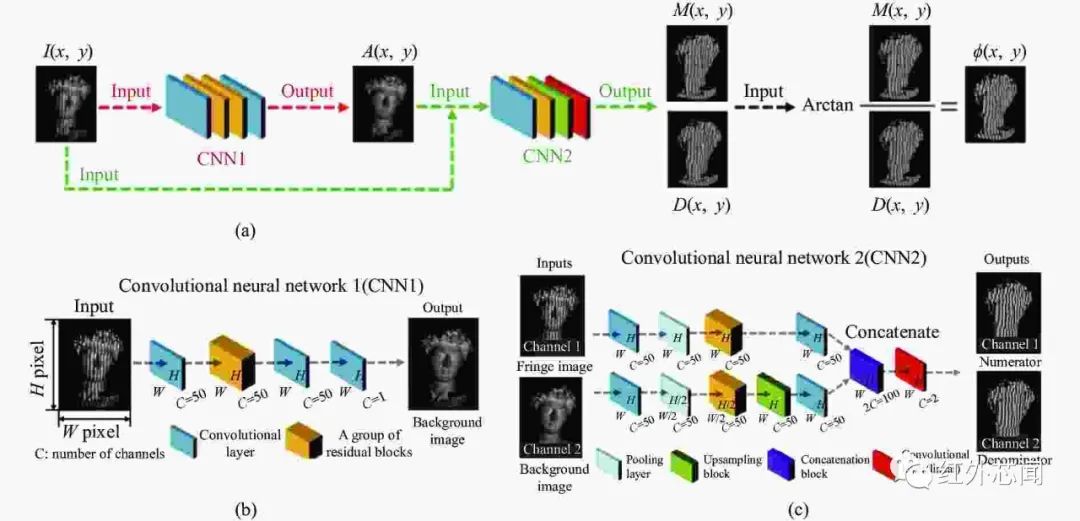
图5 (a) 文献提出方法的流程图;(b) CNN1的示意图;(c) CNN2的示意图
基于几何约束的立体相位展开可以消除相位模糊,而无需增加额外的投影图案,实现最大限度地提高相位展开的效率。Qian等提出了一种基于深度学习的几何约束相位展开方法,用于单次绝对三维形状测量,提出的框架集成了相位获取、几何约束和相位展开。该方法为高速场景下复杂物体的高精度、无运动伪影绝对三维形状测量提供了指导。但是,当图像本身存在模糊时,深度学习也不是总可以得到可靠的结果。此外,直接对投影图案进行处理,也可以实现减少总的投影图案数目,Yu等设计了一种用于深度学习的条纹图变换网络(FPTNet)。该网络可以使用更少的条纹图案(即一个或两个),得到准确的包裹相位并获得正确的绝对相位。但是,对于超快运动的物体可能会产生运动引起的误差。针对从单幅图像中获得相位展开结果进而恢复物体三维表面的问题,Qian等提出了一种基于深度学习的彩色FPP,经过适当训练的神经网络可以直接从一幅单色条纹图像预测高分辨率、无运动伪影、无串扰的绝对相位。相比传统方法,可以实现更稳健的相位展开。Li等提出了一种新的复合条纹投影深度学习轮廓术,使用提出的基于空间频率复用的条纹编码方案和网络框架,可实现单幅图案鲁棒且准确的相位展开。之后,Li等提出了一种基于深度学习的复合条纹投影轮廓术(DCFPP),可以通过训练深度神经网络实现单个复合条纹图案恢复绝对相位。Li等构建了一种独特的DNN架构,称为多尺度特征融合网络(MFFN),提出了一种从单个条纹图快速获得高精度绝对相位的方法。该方法由于只需要单个条纹图案,因此测量速度快;此外对于复杂纹理和不连续表面也具有测量精度高、鲁棒性强的优势。
上述可以有效证明深度学习是合成时间和空间信息的有效工具,突破传统单帧三维成像算法中各种影响因素的限制,有效提升测量效率和准确性。但是所需数据量较大这一问题限制了方法的可应用范围。针对这一问题,Liu等提出了一种基于深度学习的轻量级逐像素时间相位展开方法(LPTPU-DL)。由于轻量级网络的使用,训练时间可以减少到传统CNN的二十分之一,因此该方法在在训练和预测速度方面具有较强的优势,使得深度学习方法有望应用于小型快速3D系统或移动设备。Bai等提出了一种基于学习的方法来解决单频相位图的展开问题,可展开具有运动模糊、相位不连续和孤立区域的相位信息。以往基于深度学习的方法都是有监督的方法,更加适用于与训练数据类似的场景,对于与训练不同的场景则不具有普适性。Yu等提出了一种新的基于几何约束的相位展开(GCPU)方法,实现了未经训练的基于深度学习的条纹投影轮廓术,称为基于未经训练的深度学习GCPU算法。该方法比传统的GCPU具有更高的鲁棒性,且无需增加额外的条纹图案。由于测量速度较快,可以有效用于动态和高速三维测量,不足之处是该方法所需的优化过程较为复杂。
已有的研究对于深度学习的根本原因依然无法给出合理的解释,因此许多研究人员对该方法仍持怀疑态度。但是随着计算机硬件性能的不断提高,深度学习在光学计量方面实现了一定的技术突破,深度学习逐渐被越来越多的使用,成为了一种解决问题的手段和有效方法,也在光学领域发挥着越来越重要的作用。总结已有的方法和成果,深度学习用于相位展开中具有以下优点:1)条纹图案数量少;2)对复杂纹理和不连续表面的敏感性较低;3)测量速度快。但是对于深度学习而言,大量可靠的数据集仍然是一个亟待解决的问题。目前随着深度学习技术的发展和研究者们的不断深入研究,解决数据集的问题也可以转换为使用可靠的非监督学习方法或者使用轻量级网络,现已存在的类似研究也都处于探索阶段。
其他相位展开技术
除了保证测量精度,平衡物体三维表面测量的精度和速度是一个关键问题。利用基于数字投影仪高速图像切换率的二进制编码模式可以实现快速甚至高速三维测量,但目前大多数方案不能保证测量精度。因此针对一些特殊问题,提出一些特殊的相位展开方法,此处统称为其他相位展开技术。避免投影仪非线性对相位展开的影响可以实现提高测量精度的目的,Zhu等提出了一种时空二进制编码方法(T-SBE)。标准正弦条纹图采用基于强度的时空二进制编码规则,分为两个以上的二进制条纹图。由于投影的二值条纹图由0和1组成,因此可以有效地排除投影仪非线性对测量结果的影响,同时实现高质量的正弦波。在相同条件下所提出的时空二进制编码方法的精度与正弦条纹图投影的精度相当,并且优于大多数空间二进制编码方案。但是该方法的缺点是需要增加图像数量来完成实际的三维测量,因此使得测量需要时间较长。为了解决投影仪的非线性对测量精度的影响,Zhou等提出了一种时空二进制编码方法,对计算机生成的标准正弦条纹图进行编码。所提出的二进制编码策略具有与正弦条纹图投影相当的性能,并优于空间二进制编码方法。同样为了更好地解决现有数字投影仪的非线性问题,平衡测量精度和速度,Zhu等提出了一种时空二进制编码方法对计算机生成的标准正弦条纹图进行编码,不包含耗时的优化,具有速度优势。此外,相移算法和时间相位展开算法的结合可以实现快速、准确的三维测量。
为了克服传统相位展开存在的问题,各类基于几何约束的相位展开方法被相继提出。Zhong等提出了一种立体相位展开的方法,基于相移和三角张量,仅基于双摄像机、单投影仪结构光系统的几何约束,直接在两个包裹相位图之间建立一对一的对应关系。但是该方法对高频相位误差较敏感。由于双频(或双波长)方法存在的主要问题之一是对噪声的敏感性。因此,在噪声严重的应用中,通常使用3个或更多频率的相移算法代替双频相移算法。Hyun等为了实现在不增加图案数量的情况下更好完成相位展开,提出了一种几何约束的方法,通过使用一个以上周期的等效相位图进行时间相位展开,有效减少了噪声的影响。An等提出了一种利用结构光系统的几何约束生成的人工最小相位图逐像素展开相位的方法。与传统的时间相位展开不同,所提出的绝对相位展开技术不需要额外的图像采集,也不需要任何附加摄像头,因此该方法具有测量速度快的优势,且不会增加系统复杂性或成本。但是该方法存在的问题是测量深度范围有限。传统的数论方法作为时间相位展开的经典算法,因为要求两个条纹频率在投影坐标的全局范围内互质,所以在展开高频相位时稳定性较差;使用低频条纹图案会使得相位展开可靠性增加,但是相应的精度会有所降低。Yei等提出了一种基于几何约束的数论相位展开的动态场景高速三维形状测量方法。与传统的数论时间相位展开相比,即使在使用高频条纹图的情况下,相位展开的可靠性也可以显著提高。
此外,一些采用其他基准用于相位展开的方法也逐渐被提出。Dai等提出了一种不需要常规时间相位展开的绝对三维形貌测量方法,使用已知对象来为绝对相位展开提供信息,仅需要3个相移条纹图案即可测量沿深度方向移动物体的绝对形状。但是该方法对于参考对象与测量场景之间的关系具有一定限制。Qi等提出了一种新的光度约束用于相位展开方法(PCPU),使用了单频条纹图案,无需额外的相机,可以实现可靠的相位展开。与基于空间约束的方法相比,取得了显著的改进。新约束条件的引入可以克服传统空间约束条件的限制,使得相位展开技术可以扩展到适用于实现不同测量材料的更复杂场景中。
典型技术比较与分析
时间相位展开技术的相位展开结果具有良好的鲁棒性和准确性,也可用于测量非连续表面,因此应用范围较广。虽然空间相位展开技术测量精度相对时间相位展开技术较差一些,但是具有测量速度快的优势,可以有效用于动态物体测量。为了避免传统时间和空间相位展开技术中存在的问题,达到优势互补,结合时间和空间方法在测量时间和测量精度上取折衷,提出了时空相位展开技术。该方法测量结果达到比时间相位展开速度快,比空间相位展开精度高,但是测量精度不及时间相位展开,测量速度不及空间相位展开。为了克服传统的时间和空间相位展开技术的一些限制,基于几何约束的相位展开技术被相继提出。利用测量仪器与相位的空间约束特性实现相位展开,测量速率得到了有效的提升。但是该方法的测量深度范围具有一定的局限性,此外也会增加测量成本。引入其他新的约束条件用于相位展开的方法也在不断的探索过程中。计算机技术的发展使得深度学习越来越广泛地应用到光学计量中,深度学习可以克服传统时间相位展开技术和空间相位展开技术的不足,实现快速测量的同时保证一定的精度。但是对于不同的基于深度学习的相位展开技术也存在着一定的不足之处,比如:需要合适的数据集、训练合适的网络模型、可靠性不稳定、硬件设施要求高、需额外增加预处理和后处理步骤等。相关学者们也对部分相位展开技术做了一定的分类和对比。为了更好地对前述的相位展开技术进行说明,文中对几种典型的相位展开技术的性能进行了总结,如表1所示。
表1 典型相位展开技术对比
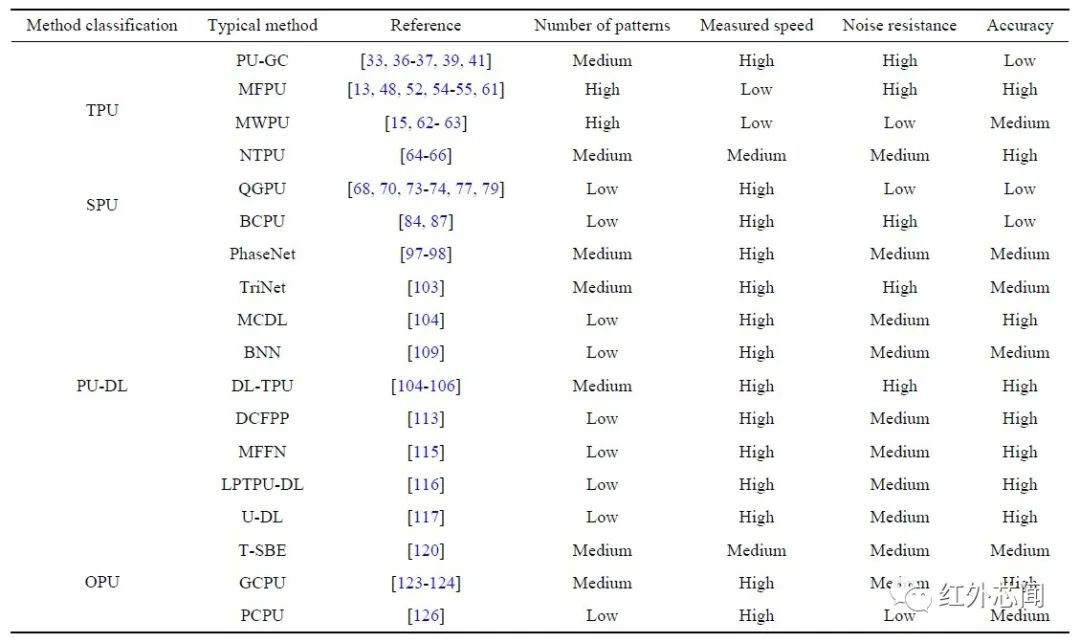
从所需的投影条纹图案数目、测量速度、抗噪性能和计算精度方面进行了比较。对表1中的相位展开技术进行以下讨论:
1)相位展开过程中所需的投影条纹图案数目。由于条纹图案上携带着空间和相位信息,对于时间相位展开而言,数目越多则测量精度越高;而空间相位展开技术则所需的图案数目较少。基于深度学习的相位展开技术和其他相位展开技术以及用于高速测量需求的相位展开技术都在趋向于减少条纹图案数目。
2)测量速度的影响因素。所需条纹图案的数目(包括是否需要增加额外的条纹投案)、测量所需的时间、计算复杂度、相位展开过程是否需要预处理和后处理步骤等,不同的方法会从一个或多个因素来加快测量速度。针对静态物体对测量速度没有明确的限制,而对于高动态物体则需要对测量速度提出更高的要求,尤其是对测量过程所需要投影条纹的数目提出了更高的要求。
3)抗噪性能是决定测量精确度和可靠性的关键因素。实际测量环境中的噪声因素不可避免,为了尽可能地减少噪声对测量结果的影响,从方法原理的抗干扰性和误差扩散、采用的条纹投影图案对噪声的抑制作用和对方法的改进中通过预处理、后处理或者滤波等方法实现增强相位展开的抗噪性能。在各类相位展开技术中,空间相位展开技术的抗噪性相对较差,从原理上空间相位展开依赖于相邻像素实现相位展开,因此对噪声较为敏感。
4)相位展开精度是决定三维测量结果精度的关键因素。针对测量精度要求高的场景,可以选择时间相位展开技术中的多频相位展开实现高精度测量,基于深度学习的相位展开技术也在一定程度上达到高精度要求。
总结与展望
时间相位展开技术多用于对测量精度要求较高,且对测量时间要求较低的测量场景中,其中相移与格雷码相结合的结构光三维测量方法也逐渐被证明可有效用于高速高动态测量。空间相位展开技术由于具有测量速度快的优势则多用于对测量速度要求较高且对测量精度要求较低的测量场景中。基于深度学习的相位展开技术则可以在一定程度上解决时间相位展开和空间相位展开技术中的不足,已有的研究逐渐证明了兼具测量效率和测量精度的相位展开技术的可靠性,但是将其广泛应用到实际测量中还存在一定的局限性。此外,针对特定的测量场景和测量需求而被提出的其他相位展开技术,比如时空相位展开、几何约束和光度约束等,这些技术也在测量精度和复杂场景测量中具有一定的突破。针对相位展开技术在条纹投影三维形貌测量技术过程中的重要性和影响精度的因素,总结未来发展方向包括以下5点:
1)减少投影图案数量
条纹图案包含着重要的相位信息,是决定相位展开成功与否的关键因素之一,较多的投影图案数量可以保证相位展开的可靠性,但是同时使得测量速度减慢,降低了测量效率。已有的减少投影图案数量的方法中,时间相位展开技术所需的投影图案数目仍然是最多的,虽然它能保证测量的精度;空间相位展开技术虽然所需投影图案数量较少,但是测量精度相对较低;基于深度学习的相位展开技术也在减少投影数目方面有一定的进展,但是仍然存在不确定性。因此减少投影图案数量的相位展开技术仍然是一个有待继续探索的挑战。
2)增强抗噪性和鲁棒性
针对复杂的测量环境和来被测物体本身的复杂程度,需要在一定程度上提升相位展开算法的抗噪性,从而提升测量的可靠性和准确性;针对低信噪比环境下的实时三维重建技术,需要提升相位展开算法的鲁棒性,从而保证测量的有效性和可靠性。
3)减小计算的复杂度
随着计算机技术的发展,计算成本问题得到了有效解决。但是计算复杂度较低的算法不仅可以节省不必要的计算成本,而且可实现在增加测量快速性的同时保证算法的可靠性,简化算法过程相比复杂的算法具有更高的可靠性和普适性。
4)提高相位展开精度
相位展开的精度对最终物体三维形貌测量结果有着重要的影响。精准测量对于精密制造等应用具有重要的意义,因此在对测量精度有较高要求的场景,保证相位展开的精度可以有效保证测量精度。在满足精度以外的其他测量要求(投影图案数目、测量速度、测量范围等)前提下,更具有普适性的高精度相位展开技术 需要进一步得到研究和发展。
5)实现高速实时测量
随着三维测量技术的广泛应用,各行各业的测量需求也在日益增加,仅可以实现静态物体测量的方法已经不能满足更高的测量需求,高速高动态物体的测量需求日益增加。为了在高速场景中实现三维测量,主要涉及可改进的方面包括:通过减少每次重建所需的图像数量来提高测量效率;通过提升硬件设备,加快投影和拍摄速度;简化计算过程,实现快速测量。
相位展开作为结构光三维测量中的一种关键技术,随着其广泛应用也被越来越多地研究和讨论。时间相位展开技术由于具有较高的测量精度而被广泛应用于测量精度较高要求的静态物体。随着快速测量需求的不断增加,将时间相位展开技术用于快速测量逐渐被研究和提出。但是由于时间相位展开测量效率的限制,将时间相位展开技术更好更有效地用于快速测量仍是一个具有挑战性的问题。空间相位展开本身具有测量速度快的优势,因此多用于一些对测量速度有要求且对测量精度要求不高的测量场景中。由于空间相位展开技术是以周围像素实现相位展开,因此更好的抗噪性和防止误差传播问题成为了完善该方法的重要研究方向。基于深度学习的相位展开技术兼具测量精度和测量速度,主要问题转移到了学习框架的选择、数据集问题和硬件设备上。在实现更有效三维测量方法的发展中,逐步将深度学习用于各类传统的相位展开技术中,并且得到较好的测量结果。更有效地完善基于深度学习的相位展开技术就要从选用更合适的模型框架、在实现准确测量的前提下可以降低使用数据集的数量等问题上提出更具有突破的方法。其他相位展开技术则是为了克服传统相位展开技术的问题,针对特殊问题提出的一类解决办法。此类技术只适用于特殊的测量场景,一般不具有普适性。相位展开的高速和高精度实现仍然是未来重点研究的领域和发展方向。
这项研究获得国家自然科学基金项目(52075147)和英国EPSRC项目(EP/P006930/1、EP/T024844/1)的资助和支持。
编辑:黄飞
-
开关电源的结构和基本原理2012-08-20 0
-
TFT-LCD的基本原理与制造技术2012-08-20 0
-
红外光的基本原理解析2020-12-15 0
-
磁悬浮技术基本原理是什么?2021-03-18 0
-
CapSense技术的基本原理是什么?它有哪些应用?2021-04-21 0
-
语音识别技术的基本原理及应用是什么?2021-05-31 0
-
RAID技术的基本原理是什么2021-10-14 0
-
红外光的基本原理2022-01-24 0
-
VoIP的基本原理与技术2009-07-31 1126
-
光导纤维导光的基本原理2010-01-26 13527
-
基于谐波辅助实现光学相位放大的基本原理2022-11-01 930
-
6.4.2.1 基本原理∈《碳化硅技术基本原理——生长、表征、器件和应用》2022-01-24 1677
-
光伏逆变器的基本原理2023-07-09 6400
-
相位噪声测试仪的基本原理、功能以及在晶振测试中的应用2023-12-18 1650
-
光隔离探头的基本原理 光隔离探头的作用2024-01-08 1431
全部0条评论

快来发表一下你的评论吧 !

