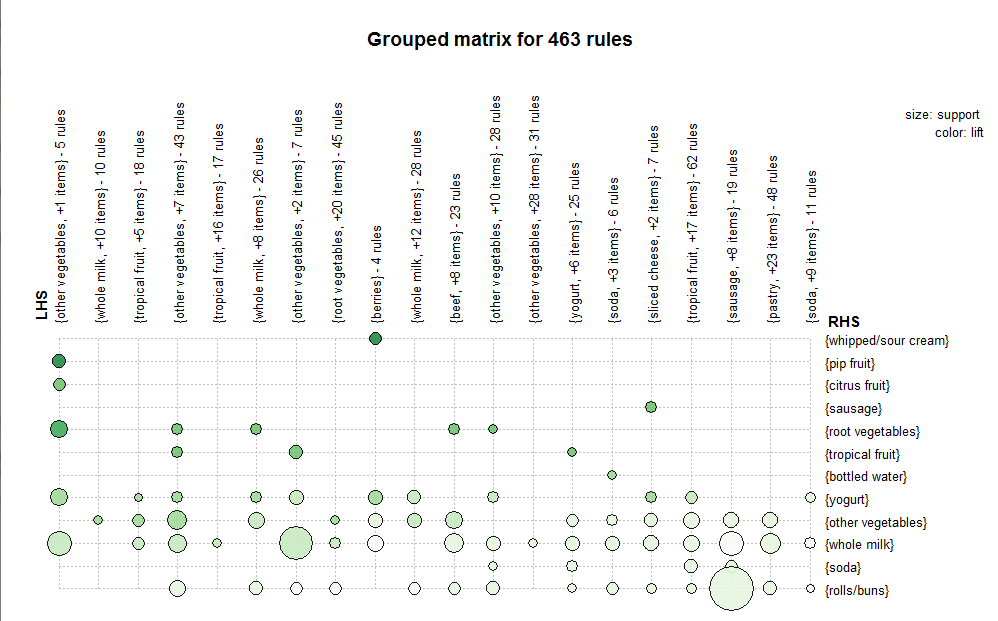
二、应用场景举例

1、股票涨跌预测

2、视频、音乐、图书等推荐

3、打车路线预测（考虑时空）

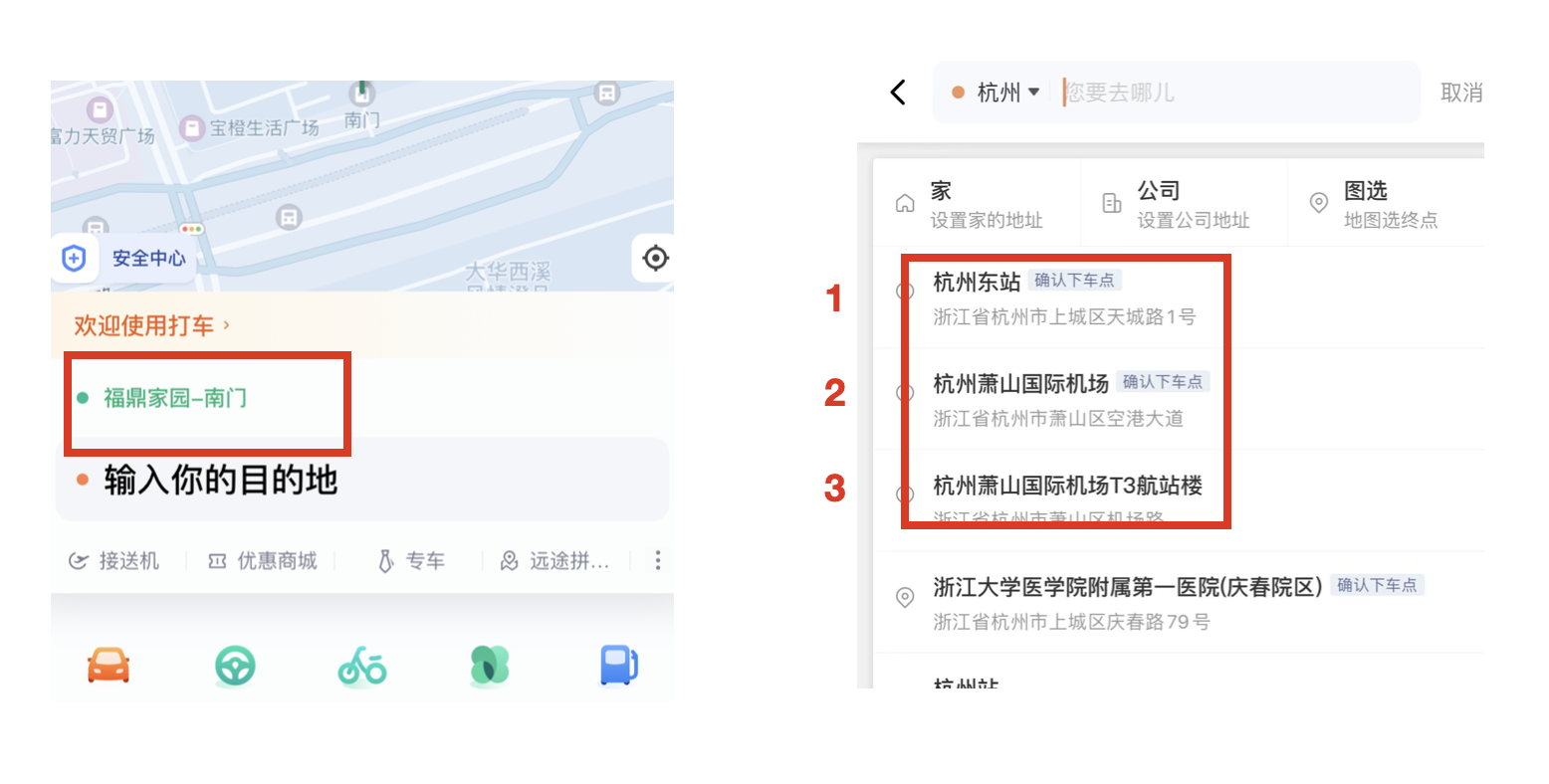
那当你每天早上打开软件的时候，打车软件就会推荐你的公司作为目的地，大大的减少用户的打车时间。如下图，我输入小区名称，马上给我推荐了三个地方，杭州东站第一位，因为平时的打车这个组合的支持度最高。

4、风控策略自动化挖掘

三、3个最重要的概念

关联规则有三个核心概念需要理解：支持度、置信度、提升度，下面用最经典的啤酒-尿不湿案例给大家举例说明这三个概念，假如以下是几名客户购买订单的商品列表：

1、支持度

在这个例子中，我们可以看到“牛奶”出现了 4 次，那么这 5 笔订单中“牛奶”的支持度就是 4/5=0.8。

这样理解起来是不是非常简单了呢，大家可以动动手计算下 '尿不湿+啤酒'的支持度是多少？

2、置信度

置信度（牛奶→啤酒）= 3/4=0.75，代表购买了牛奶的订单中，还有多少订单购买了啤酒，如下面的表格所示。

由上面的例子可以看出，置信度其实就是个条件概念，就是说在 A 发生的情况下，B 发生的概率是多大。如果仅仅知道这两个概念，很多情况下还是不够用，需要用到提升度的概念。比如A出现的情况下B出现的概率为80%，那到底AB是不是有关系呢，不一定，人家B本来在大盘中的比例95%。你的A出现，反而减少了B出现的概率。

3、提升度

• 提升度 (A→B)>1：代表有提升；

• 提升度 (A→B)=1：代表有没有提升，也没有下降；

• 提升度 (A→B)<1：代表有下降。

4、频繁项集

频繁集挖掘面临的最大难题就是项集的组合爆炸，如下图：

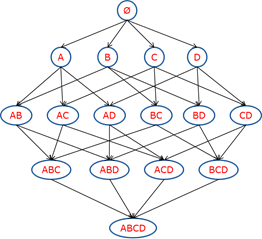
随着商品数量增多，这个网络的规模将变得特别庞大，我们不可能根据传统方法进行统计和计算，为了解决这个问题，Apriori算法提出了两个核心思想：

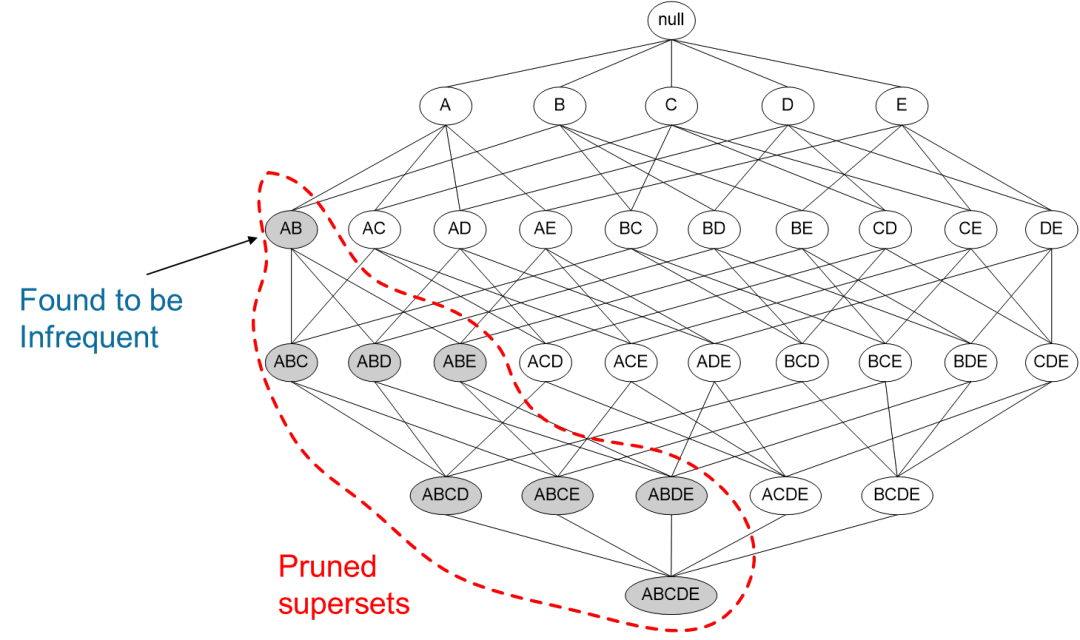
如下图，如果我们已知B不频繁，那么可以说图中所有绿色的项集都不频繁，搜索时就要这些项避开，减少计算开销。

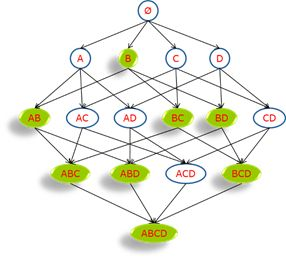
同理，如果下图所示，{A,B}这个项集是非频繁的，那虚线框后面的都不用计算了，运用Apriori算法的思想，我们就能去掉很多非频繁的项集，大大简化计算量，当然，面对大规模数据的时候，这种排除还是解决不了问题，于是还有FP-Growth（Frequent pattern Growth，频繁模式增长树）这种更高效的方法，后面有机会慢慢讲。

需要注意的是：

四、Python算法介绍

#包安装 我们使用efficient-apriori，python中也可以利用apyori库和mlxtend库
pip install efficient-apriori

#加载包
from efficient_apriori import apriori

‘’‘
apriori(transactions: typing.Iterable[typing.Union[set, tuple, list]],     
        min_support: float=0.5,     
        min_confidence: float=0.5,   
        max_length: int=8,     
        verbosity: int=0,     
        output_transaction_ids: bool=False)
上面就是这个函数的参数
min_support：最小支持度
min_confidence：最小置信度
max_length：项集长度
‘’‘

# 构造数据集
data = [('牛奶','面包','尿不湿','啤酒','榴莲'),     
        ('可乐','面包','尿不湿','啤酒','牛仔裤'),    
        ('牛奶','尿不湿','啤酒','鸡蛋','咖啡'),    
        ('面包','牛奶','尿不湿','啤酒','睡衣'),     
        ('面包','牛奶','尿不湿','可乐','鸡翅')]
#挖掘频繁项集和频繁规则
itemsets, rules = apriori(data, min_support=0.6,  min_confidence=1)
#频繁项集
print(itemsets)
{1: {('啤酒',): 4, ('尿不湿',): 5, ('牛奶',): 4, ('面包',): 4},
2: {('啤酒', '尿不湿'): 4, ('啤酒', '牛奶'): 3, ('啤酒', '面包'): 3, ('尿不湿', '牛奶'): 4, ('尿不湿', '面包'): 4, ('牛奶', '面包'): 3},
3: {('啤酒', '尿不湿', '牛奶'): 3, ('啤酒', '尿不湿', '面包'): 3, ('尿不湿', '牛奶', '面包'): 3}}
itemsets[1] #满足条件的一元组合
{('啤酒',): 4, ('尿不湿',): 5, ('牛奶',): 4, ('面包',): 4}
itemsets[2]#满足条件的二元组合
{('啤酒', '尿不湿'): 4,('啤酒', '牛奶'): 3,('啤酒', '面包'): 3,('尿不湿', '牛奶'): 4,('尿不湿', '面包'): 4,('牛奶', '面包'): 3}
itemsets[3]#满足条件的三元组合
{('啤酒', '尿不湿', '牛奶'): 3, ('啤酒', '尿不湿', '面包'): 3, ('尿不湿', '牛奶', '面包'): 3}
#频繁规则
print(rules)
[{啤酒} -> {尿不湿}, {牛奶} -> {尿不湿}, 
{面包} -> {尿不湿}, {啤酒, 牛奶} -> {尿不湿}, 
{啤酒, 面包} -> {尿不湿}, {牛奶, 面包} -> {尿不湿}]

#我们把max_length=2这个参数加进去看看
itemsets, rules = apriori(data, min_support=0.6,
min_confidence=0.5,
max_length=2)
#频繁项集
print(itemsets)
{1: {('牛奶',): 4, ('面包',): 4, ('尿不湿',): 5, ('啤酒',): 4, ('R',): 4},
2: {('R', '啤酒'): 4, ('R', '尿不湿'): 4, ('R', '牛奶'): 3, ('R', '面包'): 3, ('啤酒', '尿不湿'): 4, ('啤酒', '牛奶'): 3, ('啤酒', '面包'): 3, ('尿不湿', '牛奶'): 4, ('尿不湿', '面包'): 4, ('牛奶', '面包'): 3}}
#通过这个数据我们可以看到，项集的长度只包含有两个项了

五、挖掘实例

每个导演都有自己的偏好、比如周星驰有星女郎，张艺谋有谋女郎，且巩俐经常在张艺谋的电影里面出现，因此，每个导演对演员的选择都有一定的偏爱，我们以宁浩导演为例，分析下选择演员的一些偏好，没有找到公开的数据集，自己手动扒了一部分，大概如下，有些实在有点多，于是简化下进行分析。

可以看到，我们一共扒了9部电影，计算的时候，支持度的时候，总数就是9.

#把电影数据转换成列表 
data = [['葛优','黄渤','范伟','邓超','沈腾','张占义','王宝强','徐峥','闫妮','马丽'], 
['黄渤','张译','韩昊霖','杜江','葛优','刘昊然','宋佳','王千源','任素汐','吴京'],
['郭涛','刘桦','连晋','黄渤','徐峥','优恵','罗兰','王迅'], 
['黄渤','舒淇','王宝强','张艺兴','于和伟','王迅','李勤勤','李又麟','宁浩','管虎','梁静','徐峥','陈德森','张磊'],
['黄渤','沈腾','汤姆·派福瑞','马修·莫里森','徐峥','于和伟','雷佳音','刘桦','邓飞','蔡明凯','王戈','凯特·纳尔逊','王砚伟','呲路'], 
 ['徐峥','黄渤','余男','多布杰','王双宝','巴多','杨新鸣','郭虹','陶虹','黄精一','赵虎','王辉'], 
 ['黄渤','戎祥','九孔','徐峥','王双宝','巴多','董立范','高捷','马少骅','王迅','刘刚','WorapojThuantanon','赵奔','李麒麟','姜志刚','王鹭','宁浩'], 
 ['黄渤','徐峥','袁泉','周冬雨','陶慧','岳小军','沈腾','张俪','马苏','刘美含','王砚辉','焦俊艳','郭涛'], 
 ['雷佳音','陶虹','程媛媛','山崎敬一','郭涛','范伟','孙淳','刘桦','黄渤','岳小军','傅亨','王文','杨新鸣']]
#算法应用
itemsets, rules = apriori(data, min_support=0.5,  min_confidence=1)
print(itemsets)
{1: {('徐峥',): 7, ('黄渤',): 9}, 2: {('徐峥', '黄渤'): 7}} 
print(rules) [{徐峥} -> {黄渤}]