模型评估、模型选择和算法选择技术的正确使用

摘要：模型评估、模型选择和算法选择技术的正确使用在学术性机器学习研究和诸多产业环境中异常关键。本文回顾了用于解决以上三项任务中任何一个的不同技术，并参考理论和实证研究讨论了每一项技术的主要优势和劣势。进而，给出建议以促进机器学习研究与应用方面的最佳实践。本文涵盖了用于模型评估和选择的常见方法，比如留出方法，但是不推荐用于小数据集。不同风格的 bootstrap 技术也被介绍，以评估性能的不确定性，以作为通过正态空间的置信区间的替代，如果 bootstrapping 在计算上是可行的。在讨论偏差-方差权衡时，把 leave-one-out 交叉验证和 k 折交叉验证进行对比，并基于实证证据给出 k 的最优选择的实际提示。论文展示了用于算法对比的不同统计测试，以及处理多种对比的策略（比如综合测试、多对比纠正）。最后，当数据集很小时，本文推荐替代方法（比如 5×2cv 交叉验证和嵌套交叉验证）以对比机器学习算法。 

1 简介：基本的模型评估项和技术

机器学习已经成为我们生活的中心，无论是作为消费者、客户、研究者还是从业人员。无论将预测建模技术应用到研究还是商业问题，我认为其共同点是：做出足够好的预测。用模型拟合训练数据是一回事，但我们如何了解模型的泛化能力？我们如何确定模型是否只是简单地记忆训练数据，无法对未见过的样本做出好的预测？还有，我们如何选择好的模型呢？也许还有更好的算法可以处理眼前的问题呢？

模型评估当然不是机器学习工作流程的终点。在处理数据之前，我们希望事先计划并使用合适的技术。本文将概述这类技术和选择方法，并介绍如何将其应用到更大的工程中，即典型的机器学习工作流。

1.1 性能评估：泛化性能 vs. 模型选择

让我们考虑这个问题：「如何评估机器学习模型的性能？」典型的回答可能是：「首先，将训练数据馈送给学习算法以学习一个模型。第二，预测测试集的标签。第三，计算模型对测试集的预测准确率。」然而，评估模型性能并非那么简单。也许我们应该从不同的角度解决之前的问题：「为什么我们要关心性能评估呢？」理论上，模型的性能评估能给出模型的泛化能力，在未见过的数据上执行预测是应用机器学习或开发新算法的主要问题。通常，机器学习包含大量实验，例如超参数调整。在训练数据集上用不同的超参数设置运行学习算法最终会得到不同的模型。由于我们感兴趣的是从该超参数设置中选择最优性能的模型，因此我们需要找到评估每个模型性能的方法，以将它们进行排序。

我们需要在微调算法之外更进一步，即不仅仅是在给定的环境下实验单个算法，而是对比不同的算法，通常从预测性能和计算性能方面进行比较。我们总结一下评估模型的预测性能的主要作用：

评估模型的泛化性能，即模型泛化到未见过数据的能力；

通过调整学习算法和在给定的假设空间中选择性能最优的模型，以提升预测性能；

确定最适用于待解决问题的机器学习算法。因此，我们可以比较不同的算法，选择其中性能最优的模型；或者选择算法的假设空间中的性能最优模型。

虽然上面列出的三个子任务都是为了评估模型的性能，但是它们需要使用的方法是不同的。本文将概述解决这些子任务需要的不同方法。

我们当然希望尽可能精确地预测模型的泛化性能。然而，本文的一个要点就是，如果偏差对所有模型的影响是等价的，那么偏差性能评估基本可以完美地进行模型选择和算法选择。如果要用排序选择最优的模型或算法，我们只需要知道它们的相对性能就可以了。例如，如果所有的性能评估都是有偏差的，并且低估了它们的性能（10%），这不会影响最终的排序。更具体地说，如果我们得到如下三个模型，这些模型的预测准确率如下：

M2: 75% > M1: 70% > M3: 65%,

如果我们添加了 10% 的性能偏差（低估），则三种模型的排序没有发生改变：

M2: 65% > M1: 60% > M3: 55%. 

但是，注意如果最佳模型（M2）的泛化准确率是 65%，很明显这个精度是非常低的。评估模型的绝对性能可能是机器学习中最难的任务之一。

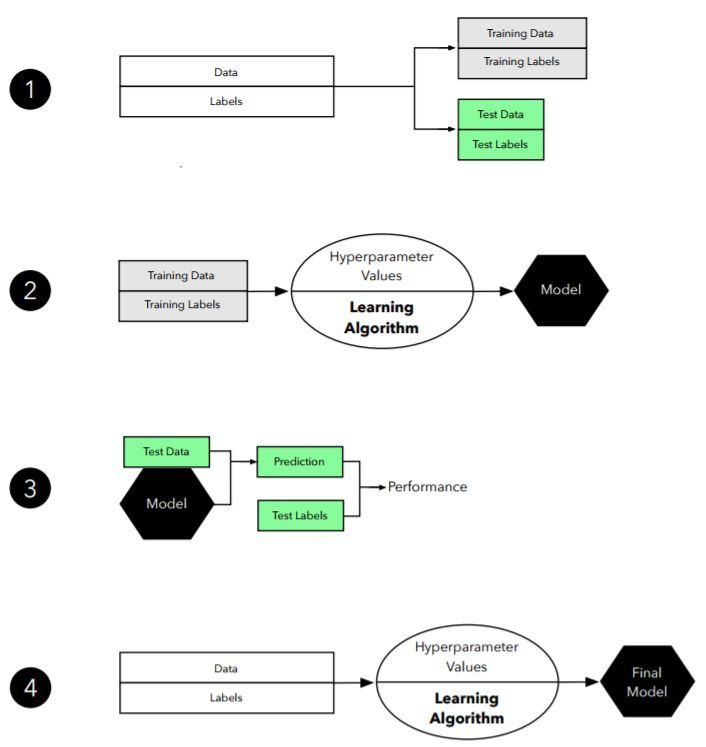
图 2：留出验证方法的图示。

2 Bootstrapping 和不确定性

本章介绍一些用于模型评估的高级技术。我们首先讨论用来评估模型性能不确定性和模型方差、稳定性的技术。之后我们将介绍交叉验证方法用于模型选择。如第一章所述，关于我们为什么要关心模型评估，存在三个相关但不同的任务或原因。

我们想评估泛化准确度，即模型在未见数据上的预测性能。

我们想通过调整学习算法、从给定假设空间中选择性能最好的模型，来改善预测性能。

我们想确定手头最适合待解决问题的机器学习算法。因此，我们想对比不同的算法，选出性能最好的一个；或从算法的假设空间中选出性能最好的模型。

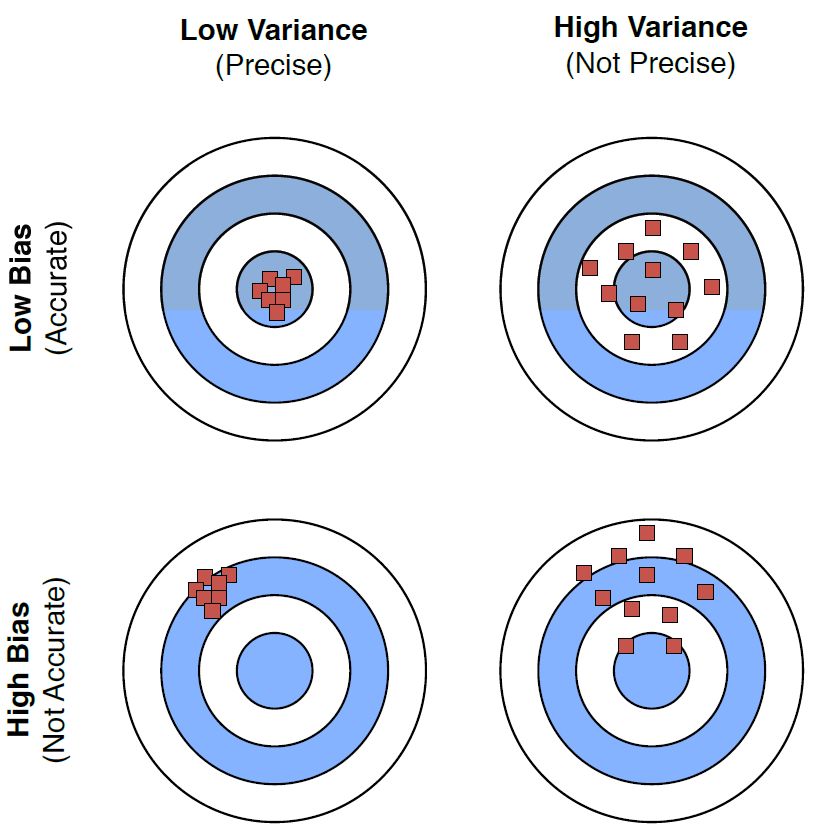
图 3：偏差和方差的不同组合的图示。

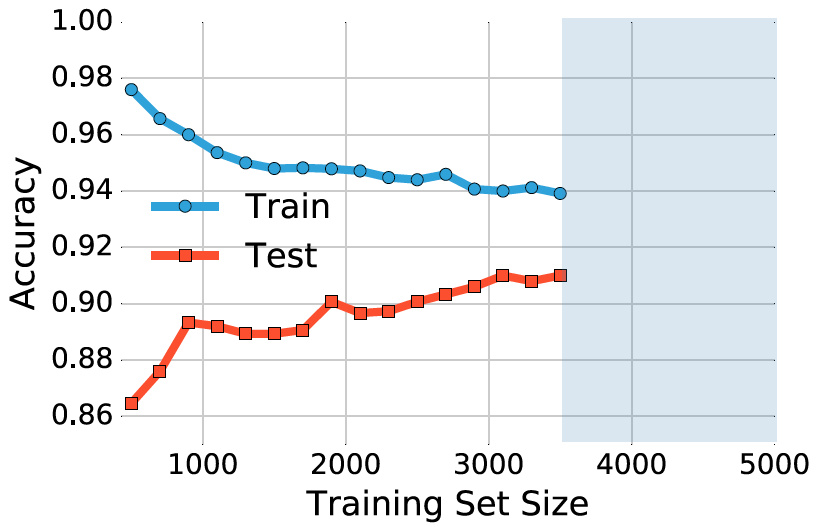
图 4：在 MNIST 数据集上 softmax 分类器的学习曲线。

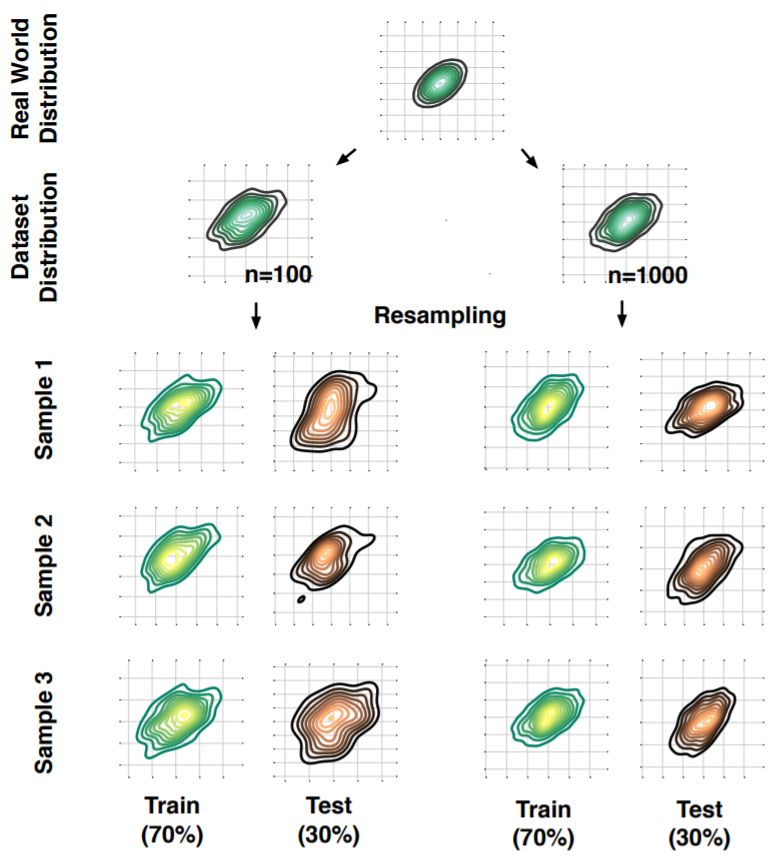
图 5：二维高斯分布中的重复子采样。

3 交叉验证和超参数优化

几乎所有机器学习算法都需要我们机器学习研究者和从业者指定大量设置。这些超参数帮助我们控制机器学习算法在优化性能、找出偏差方差最佳平衡时的行为。用于性能优化的超参数调整本身就是一门艺术，没有固定规则可以保证在给定数据集上的性能最优。前面的章节提到了用于评估模型泛化性能的留出技术和 bootstrap 技术。偏差-方差权衡和计算性能估计的不稳定性方法都得到了介绍。本章主要介绍用于模型评估和选择的不同交叉验证方法，包括对不同超参数配置的模型进行排序和评估其泛化至独立数据集的性能。

本章生成图像的代码详见：https://github.com/rasbt/model-eval-article-supplementary/blob/master/code/resampling-and-kfold.ipynb。

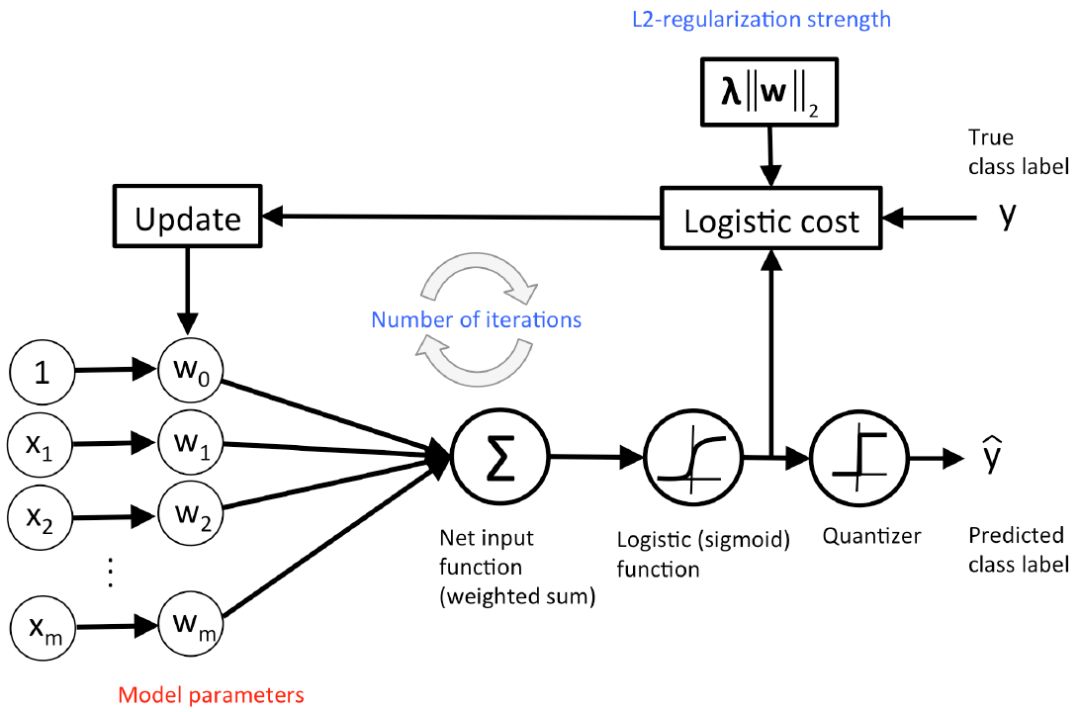
图 11：logistic 回归的概念图示。

我们可以把超参数调整（又称超参数优化）和模型选择的过程看作元优化任务。当学习算法在训练集上优化目标函数时（懒惰学习器是例外），超参数优化是基于它的另一项任务。这里，我们通常想优化性能指标，如分类准确度或接受者操作特征曲线（ROC 曲线）下面积。超参数调整阶段之后，基于测试集性能选择模型似乎是一种合理的方法。但是，多次重复使用测试集可能会带来偏差和最终性能估计，且可能导致对泛化性能的预期过分乐观，可以说是「测试集泄露信息」。为了避免这个问题，我们可以使用三次分割（three-way split），将数据集分割成训练集、验证集和测试集。对超参数调整和模型选择进行训练-验证可以保证测试集「独立」于模型选择。这里，我们再回顾一下性能估计的「3 个目标」：

我们想评估泛化准确度，即模型在未见数据上的预测性能。

我们想通过调整学习算法、从给定假设空间中选择性能最好的模型，来改善预测性能。

我们想确定最适合待解决问题的机器学习算法。因此，我们想对比不同的算法，选出性能最好的一个，从算法的假设空间中选出性能最好的模型。

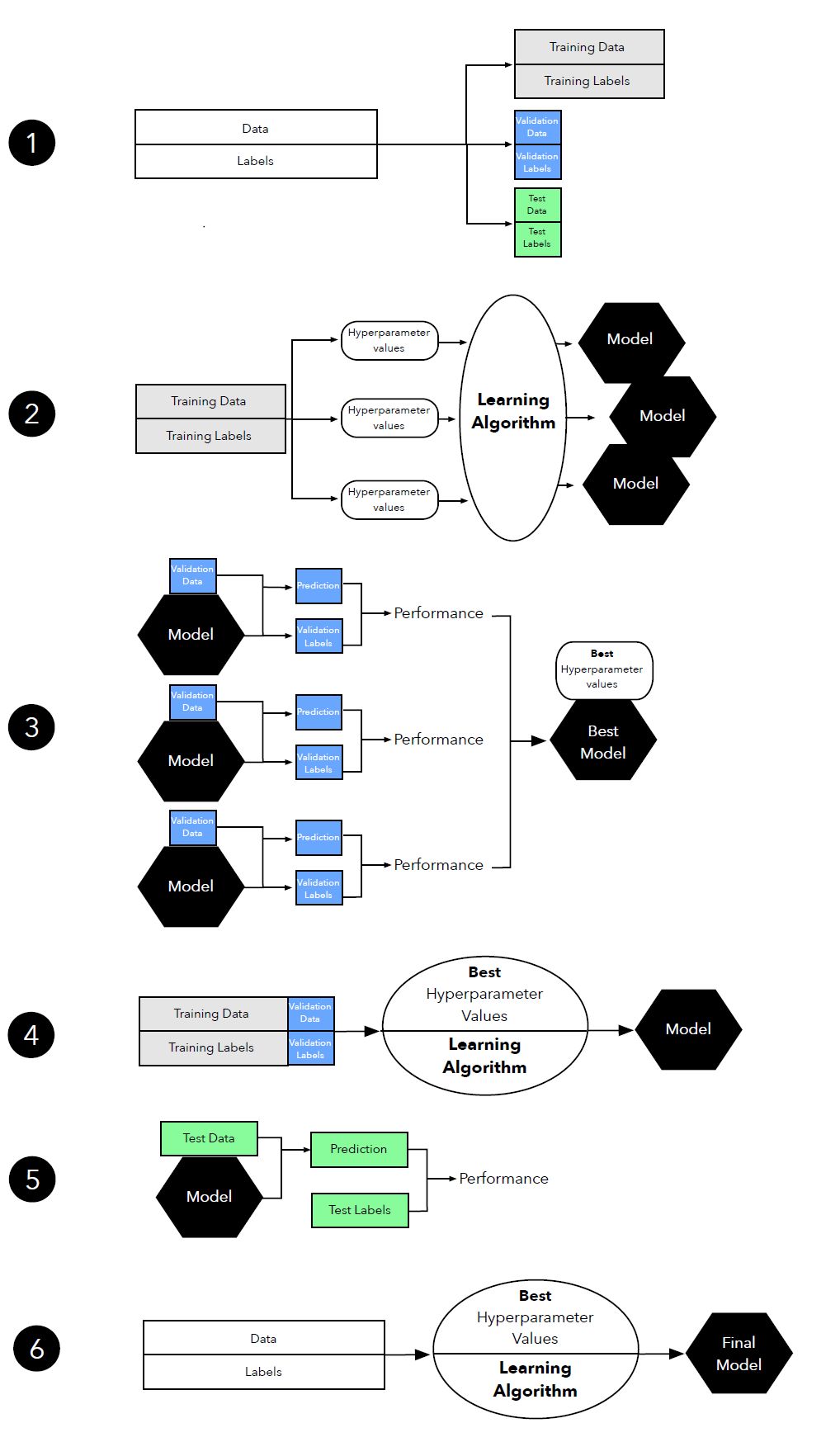
图 12：超参数调整中三路留出方法（three-way holdout method）图示。

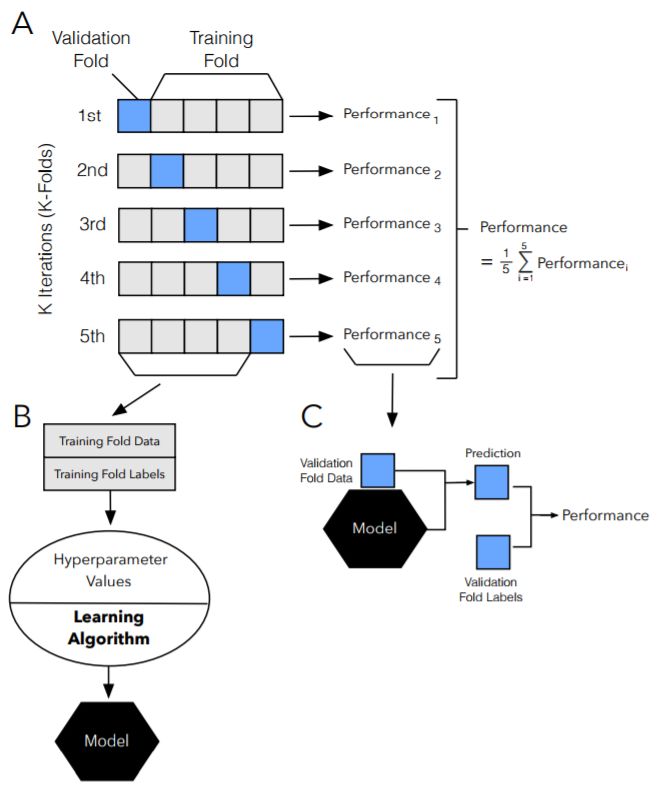
图 13：k 折交叉验证步骤图示。

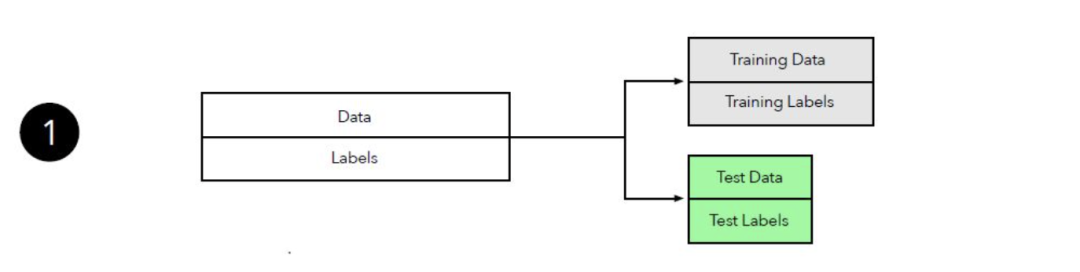
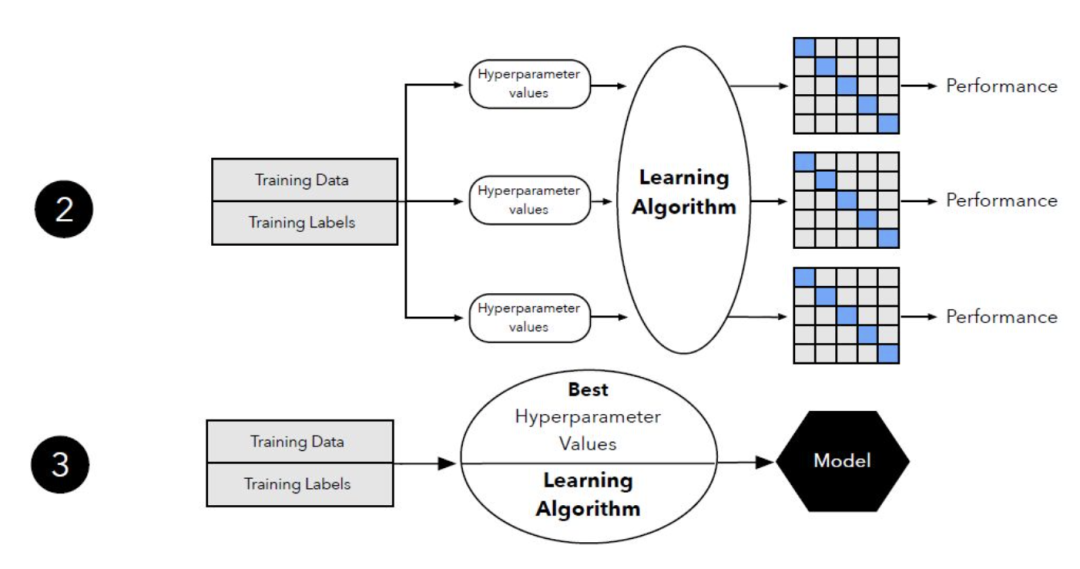
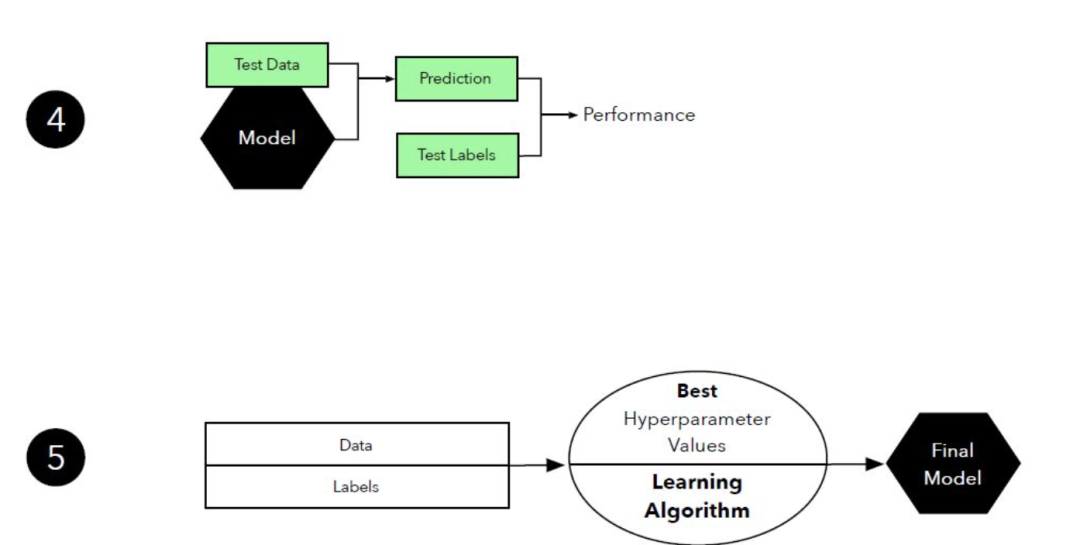
图 16：模型选择中 k 折交叉验证的图示。