

常见全波电磁仿真方法介绍与比较
描述
一
后摩尔时代我们所遇到的瓶颈 后摩尔时代,IC技术瓶颈主要有如图 1-1所示的四点。其中,IC瓶颈之一、之二和之四均取决于高效准确的电磁设计。

图1-1 后摩尔时代IC技术瓶颈 传统的基于准静态的寄生参数提取算法,由于无法处理趋肤效应,无法捕捉互连线的频变效应,无法捕捉电场-磁场耦合效应(如图 1-2),所以其仿真精度不够,需要使用全波电磁仿真方法。
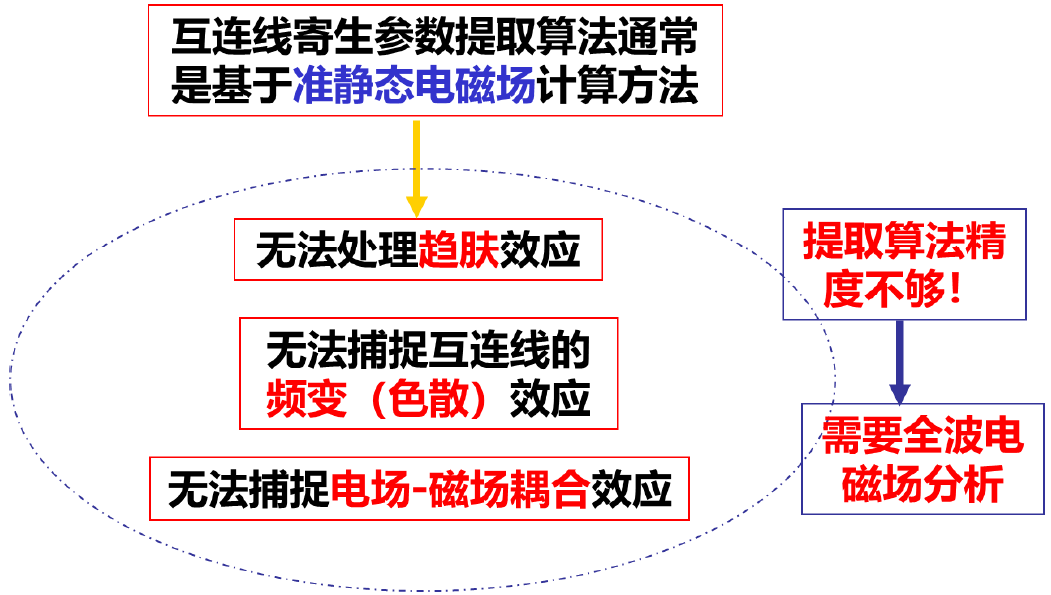
图1-2 准静态电磁计算的不足
二
常见全波电磁仿真方法介绍与比较
全波电磁仿真方法很多,图 2-1做了一个归类。在众多方法中,有限元(Finite Element Method, FEM)和矩量法(Method of Moment, MoM)是最有代表性的两种方法。FEM基于麦克斯韦方程的微分形式,该方法使用体剖分进行空间的全域离散,所以会产生较多的剖分单元。而MoM方法基于麦克斯韦方程的积分形式,可以使用面剖分或体剖分进行目标物体的离散,其生成的剖分个数远小于FEM。
图 2-2给出了体和面剖分基本单位形状。
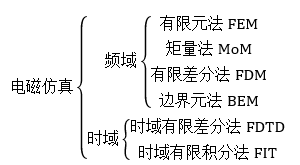
图 2-1 电磁仿真方法

图 2-2 剖分基本单元形状
图 2-3给出了不同算法的应用场景。传统的MoM和FEM方法由于计算效率问题,都只适用于较小规模的电磁问题。虽然MoM生成的未知数个数会远小于FEM,但是,MoM生成的矩阵是一个稠密矩阵,其直接求解的计算复杂度为O(N3),即使使用迭代求解,每一次迭代其计算复杂度依然高达O(N2)。所以,一般可以采用基于MoM的快速算法减小计算复杂度,加速求解过程,并扩大求解规模。如果问题进一步扩大,则只能使用一些近似算法,如物理光学(Physical Optics, PO)或几何光学(Geometric Optics, GO)进行近似计算,这些方法主要用于超大电尺寸的物体散射问题。
进一步把问题聚焦于芯片的电磁仿真领域,虽然FEM、MoM及时域有限差分法(Finite Difference Time Domain, FDTD)等计算电磁方法都能用于芯片仿真。但是相对于基于微分方程的FEM和FDTD,目前专用的芯片电磁仿真软件基本都基于积分方程MoM法,比如Cadence和Keysight的芯片版图专用电磁仿真工具。虽然一些通用的电磁仿真软件(比如基于FEM的通用仿真软件)也能用于芯片电磁仿真,但是通用电磁仿真软件与芯片设计软件没有很好的交互,且基于FEM的软件需要施加边界条件,增加了使用的复杂度。更重要的,对于介质金属层层堆叠的芯片结构,FEM、FDTD等基于偏微分方程的数值算法需要对多层介质环境进行剖分,导致求解未知数巨大;而MoM可以把介质效应放到平面分层格林函数(Layered Medium Green’s Function)中,这样只需要对金属层进行表面网格剖分,相比FEM、FDTD等算法,MoM可以大大减少了求解未知数。
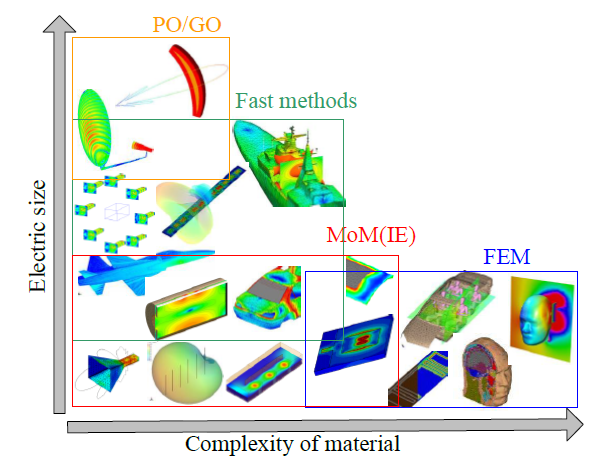
图 2-3 几种算法的应用范围
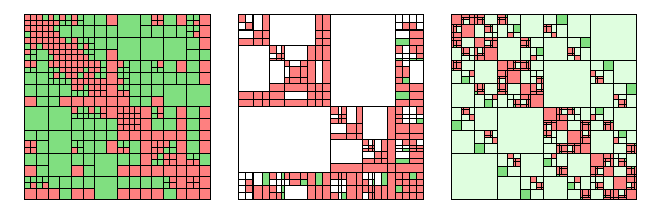
图 2-4 H-矩阵算法(绿色表示满足H-Matrix 稀疏化存储的矩阵单元)
然而对于大规模芯片问题,即使使用平面分层格林函数,MoM 生成的稠密矩阵方程的求解依然非常慢。随着多种快速低秩分解方法的提出,快速直接求解(Fast Direct Solver)方法在电磁计算领域得到了很大发展。利用相互分离的基函数组之间的低秩特性,直接求解方法将系统矩阵分割压缩成多层稀疏化表示形式。多层自适应交叉近似(Adaptive Cross Approximation Algorithm, ACA)矩阵分解算法、H 矩阵法(如图 2-4 示)和多层UV 方法等都是基于矩阵压缩的算法,但是直接对矩阵进行操作,压缩程度跟矩阵状态相关。另外,虽然直接法近些年发展很快,但是直接法的计算规模尚远不足以比拟快速迭代算法,且面向复杂工程需求,仍有很多亟待解决的挑战。
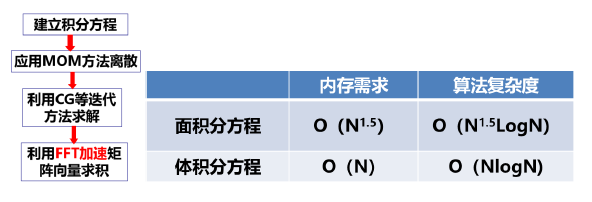
图 2-5 基于FFT的算法
使用快速迭代求解,是解决MoM稠密矩阵方程求解的另一种有效路径。比如基于快速傅里叶变换(FFT)的方法,如图 2-5所示。但是,对于面积分方程求解,为了实现FFT算法,该方法需要增加许多补零,导致效率降低。三
法动科技的高效电磁仿真技术

图 3-1 20世纪最伟大的十大算法
快速多极子(Fast Multipole Method, FMM)作为20世纪最伟大的十大算法(如图 3-1所示)之一被用于包含电磁计算在内的多种应用中。该方法而后进一步被拓展成更高效的多层快速多极子(Multi-level Fast Multipole Algorithm, MLFMA),它将整个场分为近场区和远场区重新组合加速矩阵-向量乘法,并将迭代方法的计算复杂度降低为O(NlogN),极大地提高了仿真效率,扩大了仿真规模(如图 3-2所示)。
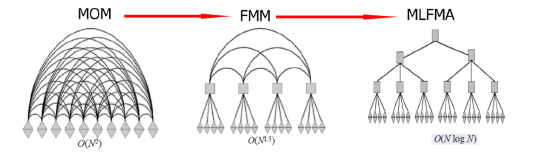
图 3-2 从矩量法发展到多层快速多极子算法计算复杂度的变化
法动科技作为射频EDA行业的领先者,自主开发了一种新的MLFMA用于芯片的电磁仿真,该方法可以同时适用于平面分层格林函数这类复杂的核函数。即使使用平面分层格林函数来减少未知数的情况下,依然可以得到O(NlogN)的计算复杂度,极大地提升芯片电磁仿真的效率。
法动科技: 成立于2017年。作为拥有硅谷及斯坦福创新基因的国际一流团队,我们专业提供射频微波电子设计自动化(EDA)软件,凭借自主研发的大容量、快速三维全波电磁仿真引擎和基于人工智能技术的高效系统级仿真引擎,能够在射频微波芯片、封装、高速PCB等领域为用户提供快速准确的电磁仿真、建模及优化设计方案。 同时,我们可以为包括移动通信、物联网、5G、雷达、卫星通信系统和高速数字设计在内的产品提供高水平设计开发服务。
审核编辑 :李倩
-
求,电磁波 仿真 软件2013-08-10 0
-
比较电磁波和引力波2019-07-02 0
-
基于Matlab的平面电磁波的传播、极化、反射和折射仿真设计2019-07-04 0
-
电磁波的介绍与比较2006-04-16 1516
-
基于Matlab的均匀平面电磁波的仿真2014-01-09 31948
-
全三维电磁仿真软件 IMST Empire XCcel简介2017-11-23 1428
-
电磁波治疗仪的作用及危害_电磁波治疗仪禁忌_电磁波治疗仪的使用方法2017-12-16 175980
-
小波去噪方法及步骤_小波去噪方法的比较2018-01-10 44329
-
如何通过电磁仿真模拟真实电磁波2018-02-14 9983
-
什么是电磁波?电磁波常见问题2022-12-19 3300
-
全波整流威廉希尔官方网站 的仿真分析2023-03-08 2899
-
电磁波如何探测?2024-01-03 2697
-
不同频率频段的电磁波的调制解调方法都不同吗?2024-01-04 1220
-
全波整流和半波整流的电压比较2024-08-14 1665
-
全波整流威廉希尔官方网站 与半波整流威廉希尔官方网站 的比较2024-10-11 1393
全部0条评论

快来发表一下你的评论吧 !

