分布式能源并网逆变器小信号稳定性分析

摘  要：随着分布式新能源大规模接入电网，并网逆变器不具备惯性和阻尼给电网安全稳定运行增加了相当大的难度。虚拟同步发电机（VSG）为分布式能源友好并网提供了惯性和阻尼支撑，但是合理设计系统主要参数才能有效保证系统的安全稳定运行。为了全面分析 VSG 主要控制参数对系统控制性能的影响，根据 VSG 控制原理建立有功调频、无功调压数学模型，并基于稳态工作点小信号模型结合控制理论分析在下垂系数、转动惯量和虚拟阻尼、滤波时间参数变化的特征根分布来判断对系统性能的影响。分析结果表明，系统稳定需要提供一定的转动惯量且必须有有功下垂特性和阻尼特性，通过合理调节VSG控制参数可以提高系统的稳定性和动态性能。最后针对参数选择进行总结，为系统设计选择参数提供了参考。

0 引 言

当今面临能源和环境双重危机，构建低碳、高效、清洁的能源体系成为未来世界能源发展的趋势，尤其是风、光等分布式能源在电网中占比将会大幅提升[1⁃2]。分布式能源出力具有间歇性和波动性，而其用于大量并网的逆变器由于缺乏惯性和阻尼支撑，对电网的安全稳定运行造成非常不利的影响[3⁃4]。虚拟同步发电机（VSG）技术对于传统同步发电机进行机理模拟，增加系统惯性并改善电网电压和频率的调节能力，成为目前大规模消纳分布式能源并网的有效解决方案[5⁃6]。

近年来，随着微网的迅速发展，VSG 技术受到越来越多的关注。文献[7⁃9]在多能互补微网中基于 VSG 控制可再生能源协同储能装置，通过系统改进的转动惯量调节方案，实现分布式能源在微网不同运行模式的频率稳定性控制。文献[10⁃12]利用 VSG 控制的灵活性，通过建立并网逆变器的 VSG 小信号模型分析参数自适应调节的优化控制策略，进而分析采用 VSG 控制技术能有效缓解分布式能源并网带来的电网冲击。

调节方案，实现分布式能源在微网不同运行模式的频率稳定性控制。文献[10⁃12]利用 VSG 控制的灵活性，通过建立并网逆变器的 VSG 小信号模型分析参数自适应调节的优化控制策略，进而分析采用 VSG 控制技术能有效缓解分布式能源并网带来的电网冲击。

1 VSG 威廉希尔官方网站 拓扑及数学模型

1.1 VSG 控制的逆变器拓扑结构

本文研究的电压型 VSG 并网系统如图 1 所示，分布式能源储能系统通过逆变接口并入电网，主要包括 PQ功率外环、VSG 控制和电压电流双环跟踪环节，根据采集到的并网端输出电压和电流信号，通过 PQ 计算和VSG 控制模块产生电压参考指令 Uref和角频率 ω0；再由电压电流双环跟踪 Uref得到 U* 调制并网逆变器元件所需的 SPWM 驱动信号，最后通过逆变器控制分布式储能单元调节功率，并保证电压、频率稳定。其中：Lf为滤波电感；Cf为滤波电容；PCC表示公共连接点。

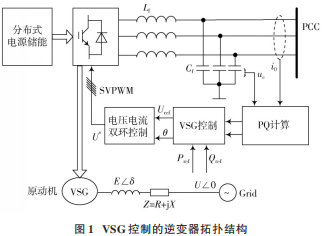
在逆变器中引入 VSG 控制策略，使其具有等同于传统同步发电机的运行特性，加强系统的有功调频（Pe⁃ω）和无功调压（Q⁃E）能力，从而提高微网运行稳定性。

1.2 有功调频（Pe⁃ω）控制

借鉴同步发电机调速器原理和转子运动方程模拟VSG 控制的一次调频特性及转动惯性。当电力系统中有功负荷突变引起同步发电机有功功率不平衡，导致系统频率变化时，同步发电机转动惯量和阻尼特性的存在能够使电力系统在一次调频过程中频率得到缓冲，根据有功功率和频率的变化关系，调节功率大小直至达到新的功率平衡状态。

根 据 VSG 控 制 原 理 ，同 步 发 电 机 的 机 械 运 动 部分为：

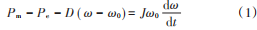
式中：Pm，Pe 分别为来自于原动机的机械功率和电磁功率；J 为虚拟转动惯量；D 为虚拟阻尼系数；ω0，ω 分别为同步角频率和机械角频率。

对比传统同步发电机调速器的原理与 VSG 一次调频过程，可将 Pm表示为有功功率下垂特性：

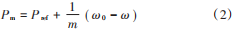
式中：m 为有功下垂系数；Pref为给定有功功率。结合式（1）、式（2），VSG 的 Pe⁃ω特性可表示为：

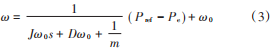
如图2 所示，基于Pe⁃ω 控制为并网逆变器增加了虚拟惯性和阻尼环节，当系统频率发生波动时，由输入系统的频率偏差自动参与完成频率调节过程。

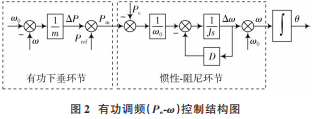
1.3 无功调压（Q⁃E）控制

当系统无功负荷发生突变时，同样会导致无功功率变化，从而引起系统电压的波动。类似于同步发电机励磁调节过程，VSG 通过提供无功功率来维持电压稳定。VSG 无功⁃电压（Q⁃E）控制为：

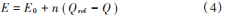
式中：E0为给定参考电压；Qref为给定无功功率；n 为 Q⁃E的下垂系数。

无功调压（Q⁃E）控制过程如图 3所示。

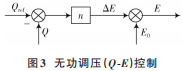
2 VSG 小信号模型

逆变器作为分布式电源并网的重要连接装置，具有控制灵活和响应迅速的特点，但其对于负荷波动具有较强的敏感性。当系统受扰动后频率易产生振荡，通过小信号建模来分析系统稳定性是目前常用的方法。根据图 1 中 R + jX 为输出虚拟等效阻抗，E，U 分别为 VSG 输出电压及电网电压幅值，δ为二者的相角差，为了简化分析，忽略不计线路电阻 R 情况下，逆变器输出功率可表示为：

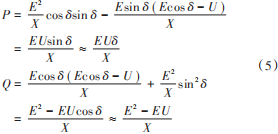
考虑线路阻抗压降较小，且线路中满足 X ≫ R，因此 U ≈ E，cos δ ≈ 1，sin δ ≈ δ，不计有功功率和无功功率间的耦合，在小信号扰动下，VSG 的 Pe ⁃ω 特性可表示为一阶惯性环节：

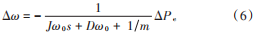
以下垂特性的微网控制，功率测量中高频部分采用低通滤波进行滤除，则有：

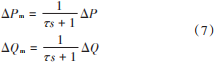
式中 τ为滤波器的时间常数。假设系统的稳态工作点为（δ0，E0，U0），分别进行小信号线性化，可得：

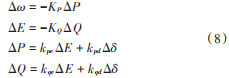
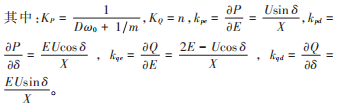
结合式（7）整理后有：

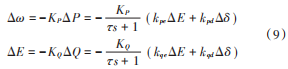
代入 Δω = sΔδ，得到：

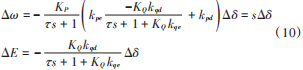
得到 VSG 并网运行特征方程式如下：

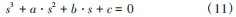
式中特征方程系数分别为：

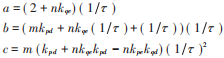
将式（8）代入式（11）可知：

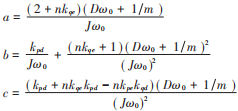
通过对特征方程的求解得到根轨迹的分布情况，对系统进行性能分析。

3 VSG 控制参数对稳定性的影响

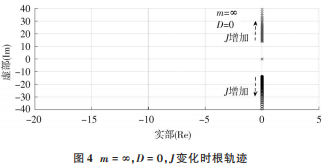
从式（11）知特征根与功率下垂系数、转动惯量、虚拟阻尼和滤波时间常数等系统关键参数相关，采用根轨迹法分析 VSG 控制参数变化对并网稳定性的影响。单机并网逆变器参数分别为：U = E =212 V，δ =0.02 rad，X =0.1 Ω，ω0 =314 rad/s。首先考虑有功频率下垂系数m 及阻尼系数 D 不起作用时，即当 m = ∞，D = 0 时，随 J的变化得到根轨迹如图 4 所示。无论 J 的取值如何变化，根均落在虚轴上，系统不稳定，因此也说明了系统须具有有功下垂和阻尼特性的必要性。

3.1 有功下垂系数m的影响

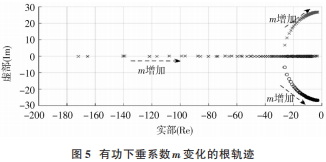
改变有功功率下垂系数 m 的值，保持其他参数不变，得到随 m 变化的系统特征根轨迹如图 5所示。

随着有功下垂系数m 的增加，系统具有的特征根s1，s2，s3均表现为往虚轴方向运动的趋势，对系统的稳定产生相当不利的影响。随着 m 的进一步增加，实轴上的特征根 s1不断靠近虚轴，而 s2，s3从实数根变为一对共轭复数根。s1，s2，s3距离虚轴越来越近，呈现为三阶系统，稳定性逐渐变差，因此在选择 m 时取值不宜过大。

3.2 无功下垂系数 n的影响

改变无功下垂系数 n 的值，其他参数则保持不变，得到系统随 n 变化的特征根轨迹如图 6 所示。随着 n 的增加，其中一个极点 s1沿着实轴向左边移动，随着 s1逐渐远离虚轴距离增加，其对系统性能的影响可以忽略。

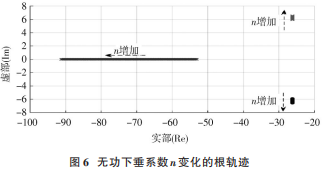
另外两个 s2和 s3为共轭复数根为主导特征根，其实部不随参数变化，虚部变化较小，即 n 的变化对并网稳定性的影响相对较小。

综合下垂系数对系统性能的影响，则主要是由有功下垂系数 m 的取值所决定。在实际应用中，m 和 n 的选择则由系统在稳态时所能承受的频率最大偏差 Δωmax和电压幅值偏差 ΔE二者决定，一般情况下，下垂系数的取值相对比较固定。

3.3 虚拟转动惯量J的影响

如图 7所示为虚拟转动惯量 J变化的根轨迹，随着 J的增加，系统的 3 个特征根 s1，s2，s3均向右移动向虚轴靠近，且当增大到一定值时，将严重影响到系统的稳定性。虚拟转动惯量 J 的变化对系统一对共轭复数根 s2，s3的影响较大，s2，s3在向虚轴靠近过程中在系统的响应过程中逐渐起主导作用，离虚轴越近，系统的稳定性下降越大，并使超调加剧，动态调节时间过程变长，因此选择参数 J时一般不宜太大。

3.4 虚拟阻尼 D 的影响

如图 8 所示为虚拟阻尼 D 变化的根轨迹，随着 D 的增加，其中实轴上 s3成为非主导特征根，其越来越向左远离虚轴，对系统的影响也是越来越弱，几乎可以忽略。另外一对共轭复数根 s1，s2成为主导特征根，由复平面进入实轴后，系统由欠阻尼状态变为过阻尼状态，超调得到抑制，系统平稳性变好，但动态响应过程变慢，且其中一个特征根 s3沿实轴向虚轴靠近，导致系统稳定性下降。在选择参数 D 时一般不宜过小也不能选择过大

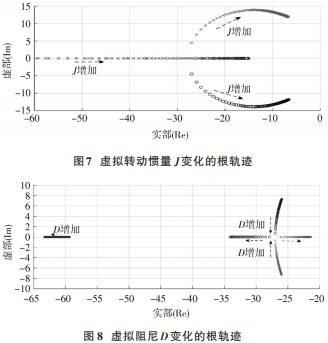
通过以上分析可知参数 J 和 D 主要决定了系统的动态性能，综合二者对系统稳定性的影响，则在 VSG 并网时，若 J 越大，D 较小时，稳定性越差，随 D 变大，系统阻尼增加，动态超调减小，响应过程速度变缓，系统的调节时间变长。因此，在选择 J 和 D 时需要折衷响应速度和稳定性二者之间的矛盾，以满足系统动态性能要求。

3.5 滤波时间常数 τ的影响

如图 9所示给出了功率滤波器时间常数 τ不同取值时的特征根轨迹。

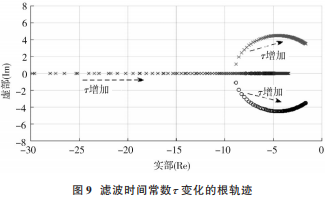
由图 9 可知随着 τ 的增大，3 个特征根明显都向虚轴靠近，系统的稳定性明显呈现下降趋势。特征根 s2，s3由实轴进入复平面快速向虚轴移动，系统阻尼也迅速减小。选择 τ 要考虑滤除输出瞬时功率中谐波成分，还要能使 VSG 控制中功率外环与电压电流跟踪控制的控制频宽加大。通过减小滤波时间常数 τ 即增加滤波器截止频率使特征根向左移动则可以提高系统稳定性。

4 结 论

并网逆变器通过引入 VSG 控制具有与传统发电机相似的外特性，但 VSG 参数选择不当则会引起系统振荡甚至失稳。VSG 控制性能受多个参数影响，本文对关键参数如虚拟惯性、阻尼系数、下垂系数及功率滤波时间常数，通过建立并网逆变器的小信号模型结合特征根根轨迹分布得出参数选择的依据，进而为分布式电源并网逆变器 VSG 参数优化提供参考。

VSG 参数具有灵活可控性，无须硬件修改，在设计时可利用根轨迹法综合考虑具体的性能指标灵活调整参数，以满足系统的稳定性和动态响应要求。

审核编辑 ：李倩