

一种基于相位靶标的摄像机标定迭代畸变补偿算法
描述
相机畸变是影响相机标定精度的关键因素。由于畸变补偿不准确,传统的标定方法不能满足要求较高标定精度的测量系统的要求。本文提出了一种基于迭代畸变补偿算法的新型相机标定方法。相机的初始参数由全场相机像素和相位标靶上的相应点进行标定。提出了一种补偿畸变的迭代算法。为了提高相位标靶的精度,还提出了一种二维拟合和插值的方法。与传统的标定方法相比,该方法不依赖于畸变数学模型,并且在复杂的畸变条件下是稳定
1 引言
相机标定是光学三维测量的第一步,也是最重要的一步,如立体视觉、条纹投影技术和偏度测量。一般有两个方面影响照相机标定的精度。一是所选相机模型的准确性。另一个是特征点在世界坐标系的定位精度。相机畸变是影响相机模型精度的关键因素。针孔模型通常用于描述一般的成像过程,它是世界上的一个三维点与相机中相应的二维图像之间的线性投影。然而,由于相机的畸变,真实的成像过程是一个非线性投影。相机镜头畸变可分为径向畸变、偏心畸变和薄棱镜畸变。通常采用基于参数的方法来补偿透镜畸变。Alvarez等人提出了一个数学模型来研究变焦镜头的畸变变化。桑塔纳-Cedres等人研究了通过最小化线重投影误差来估计畸变模型。传统的标定方法使用带有畸变参数的无限高阶多项式来表示由不同源引起的畸变。首先对初始畸变参数进行估计,然后采用基于最小二乘法的优化算法对其他摄像机参数的畸变参数进行优化。由于输入的精度对迭代优化的严格性起着重要的作用,因此摄像机标定的精度高度依赖于初始畸变参数的精度。此外,真实的畸变是由于复杂镜头系统的累积效应、相机几何误差和图像传感器的不完美形状的结果;因此,需要一个具有足够参数的模型来模拟任何可能的畸变。然而,流行的常规标定只需要采用具有径向畸变和偏心畸变的部分偏真参数的畸真模型;实验表明,一个更精细的模型将不会帮助提高精度,但也会导致数值不稳定性。因此,传统方法的应用畸变数学模型不能完全匹配实际畸变,也限制了标定精度。为了解决这一问题,研究了非参数畸变补偿方法。Thirthala[16]等人提出了一种利用多焦张量恢复径向畸变的方法;然而,这种方法是基于畸变中心在图像中心的假设,这通常不是一个可靠的假设。Hartley等人提出了一种只考虑径向畸真的无参数标定方法。Ryusuke等人提出了一种利用二元结构光补偿镜头畸变的方法,但该方法不能标定相机的内参。因此,需要研究一种灵活、稳定的方法来标定相机的内部参数、外部参数和畸变。
通常,使用一组具有已知世界坐标的二维或三维控制点或特征点作为标定过程的输入数据。与3D靶标相比,棋盘格、平面上的正方形和圆形等二维图案被频繁使用,因为它们易于制造和处理。近年来,一种二维相位靶标由于其高精度的特征检测、大量任意提供控制点和全自动过程等优点而被研究为传统平面靶标的替代品[21,22]。Xue等人提出了一种基于同心圆光栅和楔形光栅正交消失点标定的相机标定方法[23]。Liu等人引入了交叉条纹图案作为相机标定的模型平面。Ma等提出了一种以条纹图案组作为标定靶标的特征提取方法。此外,由于从正弦条纹中获得的相位对失焦图像[26,27]的影响较小,因此相位靶标可以有效地标定对焦深度小、工作距离长的相机。Schmalz等将相位靶标与经典平面靶标进行了比较,以显示相位靶标的优越性。
为了提高标定精度,研究了减小相位靶标定位误差的方法。Schmalz等人[21]提出了一种基于四个相邻像素的平滑相位值的拟合方法。Huang等[22]应用加窗多项式拟合技术对相位靶标进行了优化,并将结果与线性插值、双二次拟合和双二次拟合进行了比较。关于原理和计算过程的细节很少。实验采用窗口大小为200×200像素的窗口双边缘拟合。然而,并没有提供选择窗口大小的原因以及窗口大小对结果的影响程度。虽然实现了显著的重投影精度,但窗口大小的可行性仍需进行讨论。上述技术主要研究了标定靶标的设计和特征检测定位精度的提高。然而,目前还没有关于提高相机畸变的补偿精度和优化具有相位靶标的相机模型的研究。
本文提出了一种基于迭代畸变补偿算法的新型相机标定方法。利用全场摄像机像素和相位靶标上的相应点来计算标定参数。可以得到基于线性投影的真实像素与重投影像素之间的畸变所引起的偏差。通过补偿偏差,可以得到一个像素的校正坐标。利用黎文伯格-马夸特算法,通过最小化校正后的坐标和重投影像素之间的差值,迭代优化标定参数。为了提高世界坐标的定位精度,提出了拟合技术和应用于相位靶标的窗口大小的可行性,以补偿任何相位误差。
02 原理和方法
2.1 相位靶标
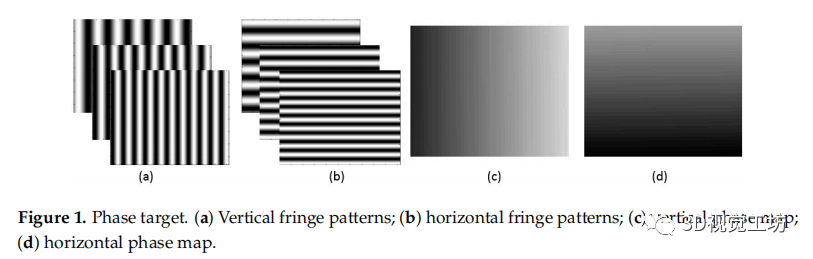
图1 相位靶标;(a) 垂直条纹图案;(b) 水平条纹图案; (c) 垂直相位图; (d) 水平相位图。
本文使用了一个相位靶标来辅助本文提出的标定方法(如图1所示)。除了在引言中所述的相位靶标的优点外,使用相位靶标的主要原因是它是一个密集和连续的靶标,并且满足了所提出的畸变补偿算法的要求。所提出的畸变补偿方法需要计算真实像素与重投影像素之间的偏差。当使用相位靶标时,摄像机像素可以根据连续的相位图,根据不同的标定姿态找到相应的世界点。虽然使用了传统的二维标定板(如棋盘),但由于相同的相机像素由于特征点有限且离散,无法发现不同标定姿态中的相应世界点,因此所提出的标定方法将会失败。两组相互垂直的移相条纹图案按顺序显示在液晶显示器(LCD)屏幕上,这些显示的图案由照相机从不同的视点捕捉到。在应用相移法和相位展开法[28–30]后,得到了两个相互垂直的绝对相位图,如图1所示。如果已知LCD像素间距的大小 和每个条纹周期的LCD像素数 ,则一个摄像机像素可以根据公式(1)和(2)的相位值唯一地定位其在世界坐标系中的相应的物理位置。

2.2 基于迭代畸变补偿算法的标定
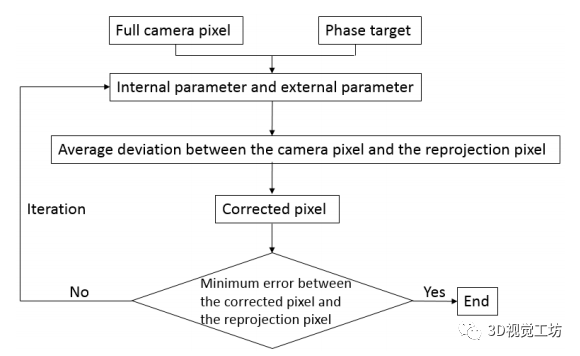
图2 我们方法的标定过程
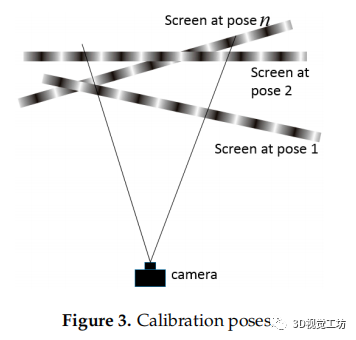
图3 标定姿势
所提出的相机标定过程如图2所示。两组正交条纹图案依次显示在液晶屏幕上。两组正交条纹图案依次显示在液晶屏幕上。在整个标定过程中,会捕获任意 幅LCD姿态的图像,如图3所示。根据每个LCD姿态,选择在CCD(电荷耦合器件)平面上均匀分布的 k 个摄像机像素,对其进行参数标定。所选的像素可以是全像素,也可以是具有相同间隙的采样像素,以提高计算速度。根据公式(1)和(2)的相位值得到相应的世界坐标。根据方程(3),可以得到一个线性投影 :
其中是相机像素坐标, 是对应的世界坐标。A是照相机的内参, 是相机主点, 是图像在 方向的缩放系数。 是刚体变换矩阵从世界坐标系到相机坐标系。让我们用 表示旋转矩阵 的第 列,用 表示线性投影 的第 列。对于已知的 、 是正交的,可以得到对内部参数的两个约束条件:
由于一个标定姿态可以根据公式(4)提供两个约束条件,因此内部参数A可以从至少三个姿态中计算出来。一旦已知A,外部参数 可以根据公式(5)计算:
在线性投影模型下,对于一个相机像素 ,畸变会导致真实坐标和重投影 的偏差:

其中: 是像素点 的相应世界坐标。由于畸变对于固定焦距的镜头和短工作距离的相机是系统误差,因此对于不同标定姿态的偏差应该是固定值。通过根据公式7使用 个位姿的平均偏差来补偿畸变,校正后的坐标 可以得到精确匹配的线性模型:

直到现在,内参A的初始值,外参 和外参 ,和畸变偏差 ,然后通过迭代循环重新计算和优化,用黎文堡-马夸特算法最小化以下函数:
2.3 相位标靶误差补偿算法
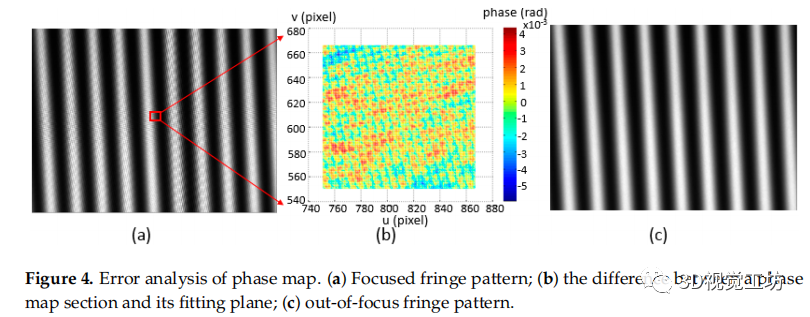
图4 相位图的误差分析。(a)聚焦条纹图案;(b)表示相位图截面与其拟合平面之间的差值;(c)离焦条纹图案。
当相位靶标放置在相机的聚焦深度时,捕获的条纹图案出现可观察的变形,如图4a所示。变形来自于液晶屏幕上记录的像素网格,以及由相机像素和液晶像素之间的干涉所产生的摩尔条纹。取计算得到的相位图中间的一个小区域,从相位值与其拟合平面的差值可以看出影响,如图4b所示。为了提高相位靶标的定位精度,保证后续标定过程的适当输入,研究了一种噪声补偿算法来对相位靶标进行细化。作为[19]中使用的虚拟散焦技术,可以应用于捕获的条纹模式。然而,很难确定过滤器的大小。消除这种影响的一种灵活的方法是,通过移动靶标位置或调整相机的对焦,将相位靶标定位在相机的失焦位置,如图4c所示。
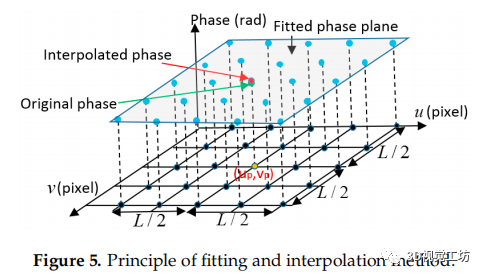
图5 拟合原理和插值方法。
由于理论上得到的绝对相位图是连续且光滑的,因此可以采用拟合和插值的方法对相位数据进行平滑处理,如图5所示。对于如图5所示的相机像素,其原始相位用图5所示的绿点表示。在相面上的点附近,相面和切面之间只有一个很小的差异。因此,可以使用最小二乘算法将一个相位平面(如图5中所示的灰色平面)与相邻的L/2像素的相位值(蓝点)进行拟合。在拟合平面的基础上,根据基于三次多项式插值的拟合平面对原始相位进行平滑,可以计算出插值的相位值(红点)。使用更大的拟合窗口(L)可以更有效地消除误差,提高相位数据的精度。但根据方程(1)-(3),得到的相图与相机像素坐标(u,v)之间的关系可以通过方程(9)和(10)得到,它们不是线性方程,因此捕获的相图是一个曲线曲面。
其中是 的逆矩阵的元素。因此,如果应用的窗口太大,窗口中的斜率数据会有明显的变化,计算点的调整会不准确。
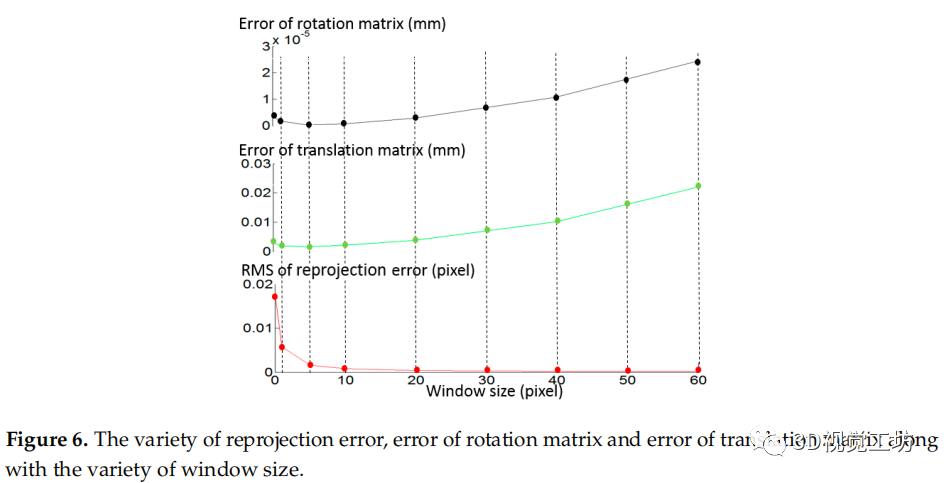
图6 重投影误差的变化、旋转矩阵的误差和平移矩阵的误差以及窗口大小的变化。
为了优化拟合窗口的大小,我们进行了一个仿真实验,如图6所示。随机相位误差是仿真过程中唯一的误差源。随着窗口大小从0(没有应用拟合和插值)增加到5个像素,重投影误差的均方根(均方根)显著降低(如红线所示)。在这个过程中,旋转矩阵R的误差和平移矩阵t的误差也都减少了(分别由黑线和绿线所示)。然而,当窗口大小从5像素增加到60像素时,虽然重投影误差的RMS从0.0016像素降低到0.000172像素,但旋转矩阵和平移矩阵的误差都增加了。仿真结果表明,5个像素是一个合适的拟合窗口大小,可以降低相位噪声,且不会过度调整原始相位值。
03 实验结果和讨论
3.1 仿真研究
仿真验证了所提出的非参数畸变补偿方法。模拟相机图像的大小为 ,主点在像素 处, 轴的尺度系数分别为3543、3522像素。径向畸变 ,偏心畸变(),薄棱镜畸变 通过公式11获取,其中、,畸变的中心为: 像素点。
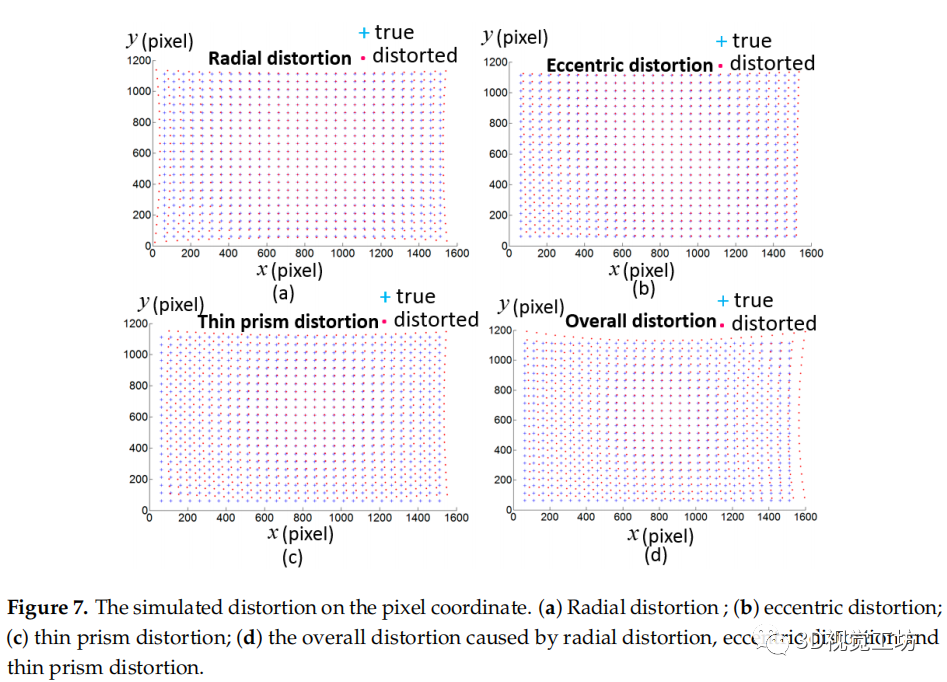
图7 在像素坐标上的模拟畸变。(a) 径向畸变 (b) 偏心畸变 (c) 薄棱镜畸变 (d) 由径向畸变、偏心畸变和薄棱镜畸变引起的整体畸变。
其中: 是理想的像素。图7显示了模拟的理想像素和畸变像素。8个位姿的位姿被仿真,其中:

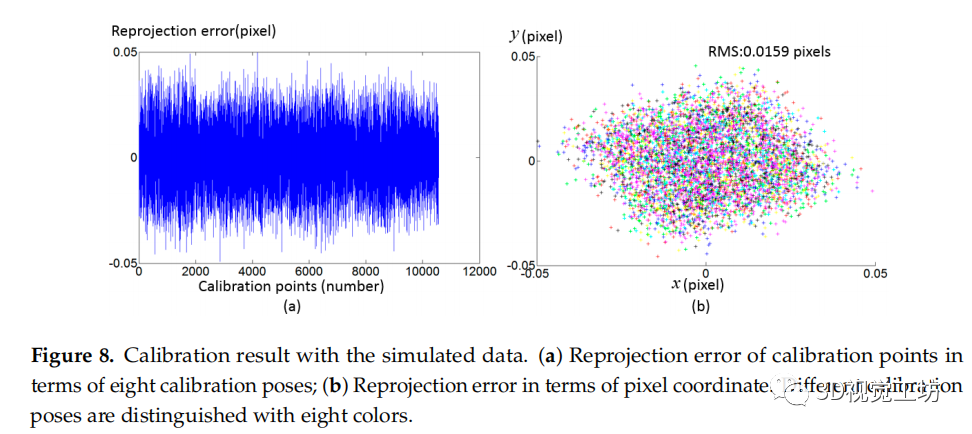
图8 与模拟数据进行标定结果。(a)八个标定点的重投影误差;(b)像素坐标的重投影误差。不同的标定姿势用八种颜色来区分。
在相位标靶中加入从0到0.005弧度的随机噪声。图8显示了所提出的标定方法的重投影误差。结果表明,该标定方法能有效地补偿复杂畸变源产生的相机畸变。
3.2 实验研究

图9 实验设置
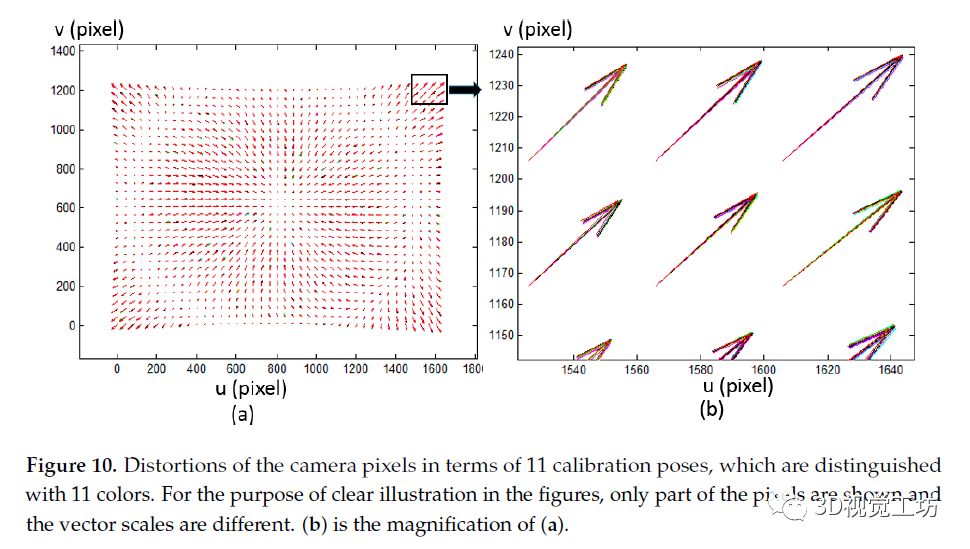
图 10. 以 11 种颜色区分的 11 种标定姿势下的相机像素畸变。为了在图中清楚说明,仅显示了部分像素并且矢量比例不同。(b) 是(a)放大倍数
为了验证提出的方法,基于Lumenera CCD相机(Model Lw235M)进行了标定实验。相机传感器的分辨率是 ,相机镜头是一个35毫米固定焦距的原始镜头。一个CCD相机(戴尔E151 Fpp,分辨率为 ,飞利浦,上海,中国)用于相位靶标。一个CCD像素块的大小为0.297mm。靶标被放置在11种不同的姿势上。采用八步相移算法和频率优化算法得到了绝对相位图[19,20],然后使用 的拟合窗口对相位图进行平滑、插值。每10个相机像素被选择形成一个大小为161×121的网格作为输入,用世界坐标中的对应点标定相机。线性投影模型下所选像素的畸变如图10所示。
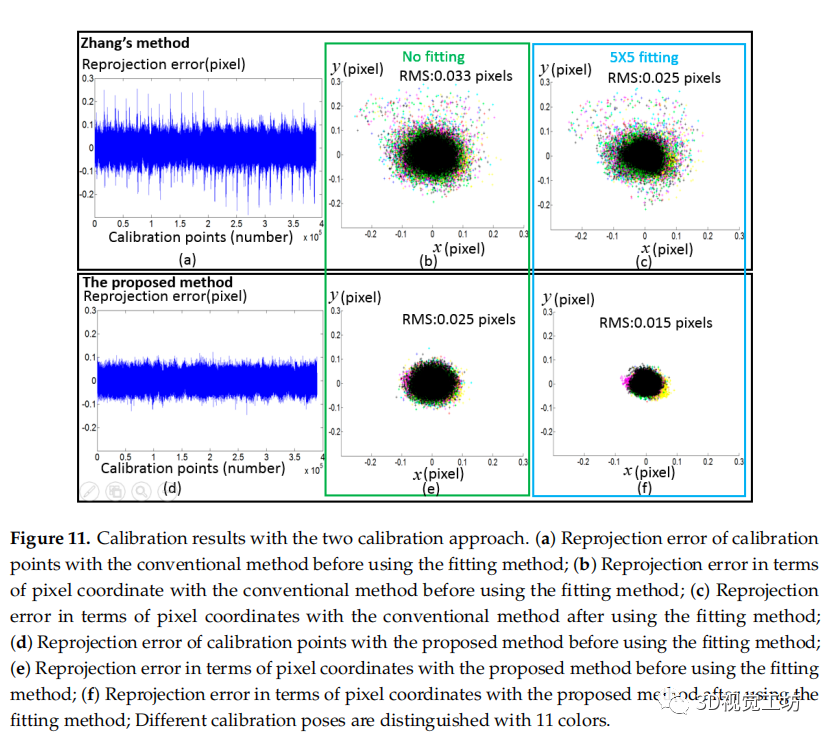
图11 标定结果采用两种标定方式。
(a) 使用拟合方法前用常规方法标定点的重投影误差;
(b) 在使用拟合方法之前,用常规方法在像素坐标方面的重投影误差;
(c) 使用拟合方法后与常规方法在像素坐标方面的重投影误差;
(d) 在使用拟合方法之前,使用所提出方法的标定点的重投影误差;
(e) 在使用拟合方法之前,用所提出的方法在像素坐标方面的重投影误差;
(f) 使用拟合方法后所提出的方法在像素坐标方面的重投影误差;不同的标定姿势用 11 种颜色区分。
由于张正友标定法[1]和相应的工具箱在实际应用中非常普遍,因此我们的方法与张正友方法对比在图11所示。张的方法可以分为四个步骤:(1)发现特征点和相机像素之间的对应位置;(2) 根据针孔模型计算相机参数和外参数的初始值;(3) 考虑基于数学模型的畸变补偿;(4)利用Levenberg-Marquardt算法优化相机初始参数、外参数和畸变参数。可以从张的文章 [1] 中使用的棋盘或其他标定靶标中检测到特征点。为避免不同标定靶标提取精度的差异,采用相同的相机像素和对应的物理点对两种方法进行测试。使用所提出的方法,重投影误差的 RMS 在应用拟合方法之前为 0.025 像素,在应用拟合方法之后为 0.015 像素。相比之下,传统方法的重投影误差的 RMS 在应用拟合方法之前为 0.033 像素,在应用拟合方法之后为 0.025 像素,分别比所提出的方法差 1.3 倍和 1.6 倍。
提出了一种基于全场相机像素和密集相位靶标的迭代畸变补偿算法的相机标定方法。为了提高相位值的定位精度,研究了散焦、拟合和插值技术。在不依赖畸变数学模型的情况下,所提出的标定方法可以获得逐像素的畸变和较高的标定精度。下一步将包括在偏转测量系统中应用的建议标定方法。
如果将所提出的方法与其他基于非参数的畸变补偿方法进行比较,那将是更可取的。然而,在这个实验中有几个不同的因素需要考虑:(1)很难获得这些方法的开放代码;(2) 其中一些方法基于特定的标定靶标,因此无法保证对比实验具有相同的标定输入。事实上,本文的仿真研究可以证明该方法的优越性,因为其他非基于参数的方法无法处理偏心畸变和薄棱镜畸变,或者无法获得内部参数相机 [18]。该仿真研究表明,所提出的方法可以有效地标定具有复杂畸变条件的相机。基于这一点,可以得出结论,该方法优于其他基于非参数的畸变补偿方法。
审核编辑:郭婷
-
基于Dragonboard 410c平台的机器3D视觉—摄像机标定原理2018-09-28 0
-
基于机器视觉的摄像机标定理论与各种方法分析2019-06-04 0
-
摄像机标定理论是什么?其方法有哪些?2021-04-13 0
-
简易摄像机标定方法2011-06-13 661
-
基于摄像机标定的车辆速度检测方法2011-11-10 752
-
一种基于Tsai法的摄像机改进标定法2012-04-26 721
-
一种基于交通视频的摄像机标定方法2012-05-29 1449
-
基于OpenCV的单目摄像机标定2017-02-08 828
-
基于OpenCV的双目摄像机标定2017-02-08 741
-
基于多视图像的摄像机自标定方法2017-11-21 716
-
基于梯形棋盘格标定板对激光雷达和摄像机联合标定方法2017-11-30 1579
-
单幅二维图像的摄像机标定方法2017-12-15 987
-
基于移动平面靶标的标定方法2018-03-15 950
-
如何使用一阶径向畸变算法进行双目摄像机多位姿标定方法2018-12-27 906
-
机器视觉的摄像机标定技术你知道多少?2023-10-16 876
全部0条评论

快来发表一下你的评论吧 !

