高速模数转换器精度的内幕

模数转换器（也称为ADC）用于许多应用，特别是需要处理模拟传感器信号的测量系统，例如用于测量压力、流量、速度和温度的数据采集系统，仅举几例。通常，这些信号是脉冲或阶跃函数形式的时域特征。

在任何设计中，了解这些类型应用的整体系统精度都很重要，尤其是那些需要量化波形中非常小的灵敏度或变化的系统。理想情况是，信号链输入端每施加一伏特，ADC以数字方式表示一伏特输出。然而，事实并非如此。与此相关的所有转换器和信号链都有一些有限的误差。

本文介绍与模数转换器本身相关的错误。它还将揭示转换器内如何积累不准确性并导致这些错误。这对于理解在为测量精度至关重要的新设计定义系统参数时如何正确指定ADC起着重要作用。最后，将讨论一个简单的误差分析，以帮助为设计选择合适的转换器。

模数转换器不准确

在任何信号链中，转换器都是系统的基础。为设计选择的任何ADC都决定了系统的总体精度。换言之，系统精度不能优于转换器的最低有效位（LSB）尺寸。为了说明这一点，应回顾ADC不准确的简短教程。

首先，请注意，由于ADC并不理想，也没有无限分辨率，因此它们只能在输出上显示有限数量的表示。表示数由转换器的输入满量程除以 2 确定N表示，N 是转换器理想情况下的位数。

例如，如果选择12位ADC，则可以在其输出端具有4096个数字表示，以表示施加到转换器输入的任何信号。这些表示确实有一些有限的误差。因此，如果12位ADC的输入满量程（VFS）为10 V p-p，则其LSB大小为2.44 mV p-p，理想情况下精度为±1.22 mV。

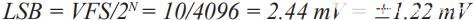
等式 1.

但实际上，ADC并不理想。有一些有限的噪音

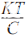
在转换器本身内，甚至在直流电中。请记住，1 kΩ电阻相当于25°C时1 Hz带宽下的4 nV/√Hz。 请注意，查看12位ADC数据手册时，SNR通常为~70 dB至72 dB。但是，如果使用以下公式，则12位ADC在理想情况下应具有74 dB：

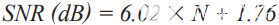
等式 2.

因此，在现实世界中，将无法实现12位分辨率，因为转换器本身存在一些与之相关的不准确性，如图2所示。

这些不准确性或误差决定了转换器在表示最终在整个信号链中采集的信号方面的效果。失调误差定义为传递函数无法通过零的模拟值。增益误差是失调误差为零时理想传递函数和实际传递函数之间的满量程值之差。通常所说的线性误差或非线性是与零电平和满量程之间绘制的直线的偏差，如图1所示。

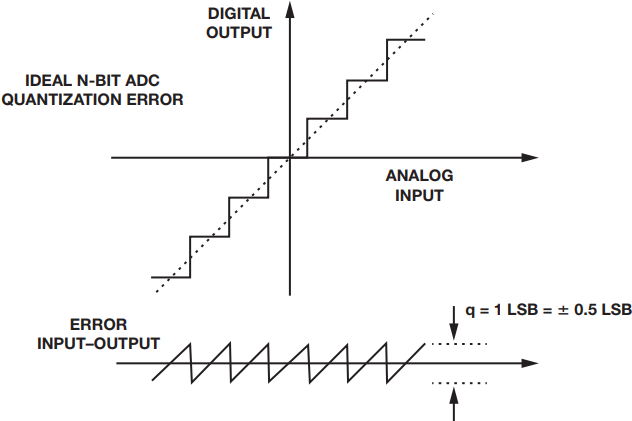
图1.ADC量化误差。

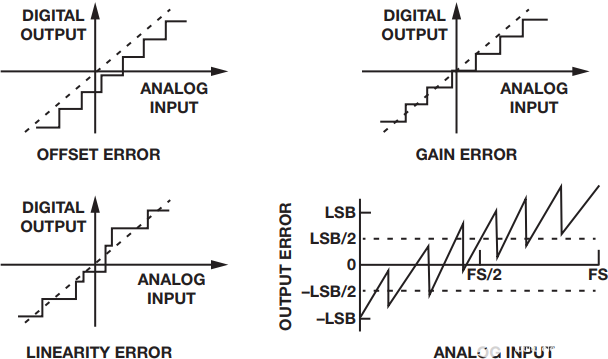
图2.ADC 不准确。

有关 ADC 不准确性的更多信息

既然已经定义并理解了最基本的模数转换器误差，那么描述这些误差之间的差异就很有用了。通常，大多数ADC具有与之相关的小失调和增益误差，因此可以通过外部模拟威廉希尔官方网站 忽略或调整（调零），或者进行数字校正。但是，线性度、量化和温度系数等其他误差无法轻松调整或消除。

模数转换器的线性度仅与转换器本身一样好，这取决于架构和工艺变化。有一些方法可以纠正这一点，但它们很昂贵。设计人员有两种选择，要么购买更好、更昂贵的转换器，要么对线性度进行数字校正。数字校正也可能很昂贵。这意味着指定DSP或FPGA可能涉及更多资源需求，因为线性度会随着温度和工艺变化而变化。根据采样速率、IF和分辨率，数字校正可能需要大量的表征和查找表，以便即时校正或调整ADC的性能。

线性度有两种类型的误差：它们是微分非线性和积分线性，通常分别称为DNL和INL。DNL 定义为与其理想值的任何误差或偏差。换句话说，它是两个相邻代码之间的模拟差值与VFS/2的理想代码值的偏差N.将此与ADC的SNR性能联系起来考虑。随着代码变体变大，转换次数会减少。该误差在整个温度范围内绑定为±0.5 LSB，以确保没有丢失代码。

INL定义为零和满量程之间与理想直线近似的曲率偏差。在大多数情况下，INL决定了ADC的SFDR性能。整体INL偏差的形状可以决定主导谐波性能。例如，INL曲线中的弓形将始终产生较差的偶次谐波，而INL曲线中的S-bow通常会产生奇次谐波。该误差本质上与频率相关，与此类误差分析无关。

即使静态失调和增益误差中的零点是可行的，与失调和增益误差相关的温度系数仍然存在。

例如，增益误差为10 ppm或FSR/°C = 0.001%/°C的12位ADC。

12 位系统中的 1 LSB = 4096 中的 1 部分，或大约 0.024%。

因此，当∆为125°C（–40°C至+85°C）时，会产生±2.5 LSB增益温度系数误差，即125 = 0.125%×为0.001%。

其中 0.125/0.024 = 5.1 或 ±2.55 LSB。

对于失调温度系数，偏移误差为 5 ppm，或 FSR/°C = 0.0005%/°C。

这将产生 ±1.3 LSB 偏移温度系数误差或 0.0005% × 125 = 0.0625。其中 0.0625/0.024 = 2.6 或 ±1.3 LSB。

模数转换器误差分析

其他误差源也可能影响转换器的性能，包括CMRR、时钟抖动、固有威廉希尔官方网站 板噪声和耦合等。所有这些误差最终决定了ADC表示信号的效率，并且通常在频域中表现得更有效。

从时域的角度来看，需要以下五个误差来决定转换器的整体精度：

相对精度，DNL，定义为 ±0.5 LSB

相对精度温度系数和DNL温度系数，通常包含在数据手册的相对精度规格中。

增益温度系数误差，为±2.5 LSB（来自上一个示例）

偏移温度系数误差，为 ±1.3 LSB（来自上一个示例）

电源灵敏度，通常以第一奈奎斯特区内的低频PSRR（电源抑制比）的形式出现。对于12位ADC，这通常表示为60 dB或±2 LSB。

只需取和方根（RSS），所有这些误差源=转换器总误差的±3.5 LSB。这似乎过于悲观。然而，统计容差可能过于乐观，或者误差总和除以误差数，或（0.5 + 2.5 + 1.3 + 2）/4 = ±1.58 LSB。找到ADC的实际容差应该介于这两种想法或方法之间。

因此，在转换器中添加精度误差，或任何精度系统分析时，设计人员应采用加权误差源方法，然后将这些误差源RSS在一起。这将提供确定ADC总误差的最佳方法。因此，±0.5 LSB的相对精度应保持在100%。但是，±2.5 LSB的增益温度系数误差应为总误差的66%，或2.5/（0.5 + 1.3 + 2）×100。±1.3 LSB的失调温度系数误差将是总误差的26%，即100×1.3/（0.5 + 2.5 + 2）。±2 LSB的电源灵敏度误差将是总误差的47%，即2/（0.5 + 1.3 + 2.5）×100。以 RSS 方式或平方根
√将这些加权误差相加（（0.5 × 1）2+ （2.5 × 0.66）2+ （1.3 × 0.26）2+ （2 × 0.47）2)，提供 ±2.0 LSB 的总误差，这会产生更现实的东西，介于上述乐观和悲观方法结果之间。

ADC 带宽精度

ADC还具有建立时间精度。请记住，转换器的内部前端需要有足够的带宽（BW）才能准确采样信号。否则，错误的累积将大于上面发现的。

一般而言，ADC的内部前端需要在半个周期或采样时钟周期（0.5/Fs）内建立，以便提供要采集的模拟信号的入站精确表示。因此，对于2.5 GSPS的12位ADC采样和1.3 V p-p的满量程输入范围，可以从以下瞬态方程开始推导出所需的全功率带宽（FPBW）：

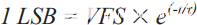
求解 t：

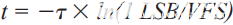
τ = 1/（2 × π × FPBW）中的子，一个时间常数，并求解 FPBW：

现在，设 t = 0.5/Fs，即样本建立所需的时间，其中采样周期为 1/Fs：

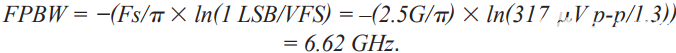
这将产生ADC内部前端或FPBW所需的最小带宽。这是转换器内部前端在1 LSB内建立并对模拟信号进行适当采样所需的带宽量。这将需要几个时间常数才能通过，以满足此类ADC的1 LSB精度。

其中一个时间常数等于 24 ps 或 τ = 1/（2 × π × FPBW）。要了解ADC满量程范围所需的时间常数，需要找到LSB大小的满量程误差%或%FS。或1 LSB = 满量程/（2N)，其中 N = 位数或1.3 V 峰峰值/（212） = 317 μV 峰峰值和 %FS = （LSB/FS） × 100 = 0.0244。

通过绘制欧拉数，或 eτ，可以开发一个图表，以便轻松显示每次常量通过时的相对误差。如图3所示，可以发现，12位ADC示例需要8.4个时间常数才能在1 LSB内适当建立。

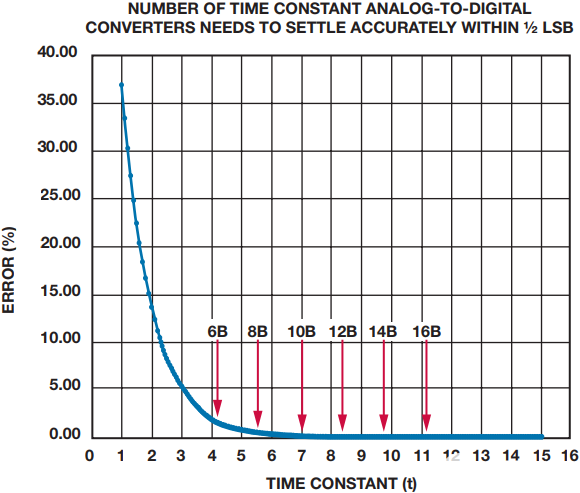
图 3：建立精度与时间常数的关系。

这允许设计人员估算转换器可以使用的最大模拟输入频率或采样带宽，并且仍建立于误差的1 LSB以内。除此之外，ADC无法准确表示信号。这被简单地定义为F.MAX= 1/（τ × 个时间常数）或 1/（24 ps × 8.4） = 4.96 GHz。

请记住，这是这里最好的情况，假设是单极点模型ADC前端。并非所有实用的转换器都以这种方式运行，但这是一个很好的起点。例如，所描述的模型在12位下有效，但是，在14位/16位及以上，应基于这些细微效应使用二阶模型，这些效应可以使建立时间超出预测的一阶模型。

关于ADC带宽的快速说明

请记住，ADC的全功率带宽与上述转换器可用带宽或采样带宽不同。这可以被视为类似于运算放大器的全功率带宽（FPBW），其中信号看起来更像一个三角形，并且其输出上存在大量失真。FPBW是ADC准确采集信号和内部前端正确建立所需的带宽（如上例所示为6.62 GHz）。选择中频并在此区域使用转换器不是一个好主意，因为系统中的性能结果差异很大，根据转换器数据手册中所述的额定分辨率和性能，全功率带宽远大于转换器本身的最大采样带宽，如~5 GHz， 上面显示的示例。样本带宽是设计的中心位置。所有设计都应避免使用额定全功率带宽的部分或全部最高频率部分，因为这样做可能会使动态性能（SNR/SFDR）降额，而降额可能会有很大差异。要确定高速ADC的采样带宽，请使用如上所示的示例，因为数据手册中有时没有特别给出。通常，数据手册指定甚至列出了生产测试频率，以保证在转换器的采样带宽内提供性能。然而，在较老的ADC中，这些测试频率并不总是显示在F上。.MAX如上文数据手册中所定义。展望未来，需要指定、定义和测试行业中对这些带宽术语的更好解释。

结论

本文应就如何查看一般静态ADC不精度误差和涉及带宽的ADC不精度误差提供一些指导。本文还进一步了解了ADC误差以及这些误差如何影响信号链。请记住，并非所有组件都是平等的，对于主动和被动设备都是如此。开发能够捕获所有这些错误的电子表格是插入不同信号链组件以更快地进行评估和组件权衡的简单方法。在权衡组件之间的成本、尺寸和功耗以及信号链性能差异时尤其如此。

在进行下一个信号链设计时，请记住这些原则。根据要求，可以向您发送电子表格分析，突出显示前面提到的示例。随意使用它并根据您的下一个设计进行定制。如果您还有其他问题，请通过ADI公司与我联系工程师专区®，一个在线技术支持社区，位于 RReeder。

关于如何生成完整信号链分析的进一步讨论将在第2部分：模拟信号链精度中介绍。最后，请记住，仅仅提高信号链中ADC的性能或分辨率不会提高测量精度。如果仍然存在相同数量的前端噪声，则精度不会提高。噪音只会被测量到更精细的程度，最终可能会花费设计师的老板更多的钱。

审核编辑：郭婷